Презентация на тему: Решение систем уравнений

  Автор: Ученик 9 «и» класса МБОУ «СОШ №7». Мансуров Артур Руководитель: Ионга Ирина Николаевна,  учитель математики,  II квалификационная категория. Решение систем уравненийПо страницам учебников А.Г. Мордковича Алгебра 7 и 9

Цель работы: . По страницам учебников А.Г. Мордковича «Алгебра 7 и 9 классов» проанализировать рассмотренные в них методы решения систем уравнений. Исследовать некоторые способы решений систем уравнений за страницами учебника.Показать своей работой, что решать системы уравнений очень просто.

Задачи работы:. выявить основные способы решения систем линейных уравнений, рассматриваемых в учебнике А.Г. Мордковича «Алгебра -7»проиллюстрировать примерами каждый способ.расширить свои познания о других способах решения систем линейных уравнений.ввести понятие систем рациональных уравнений.рассмотреть основные методы решения систем рациональных уравнений по учебнику А.Г. Мордковича «Алгебра- 9».проиллюстрировать теоретический материал удачными примерами.рассмотреть новый вид – симметрические системы.разобраться в методах решения этого вида.

Уравнение и его свойства ОпределениеУравнение – это равенство, содержащее одну или несколько переменных ax=b Линейное уравнение содной переменной ax+by=c Линейное уравнение сдвумя переменными Свойства уравненийесли в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данномуесли обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному

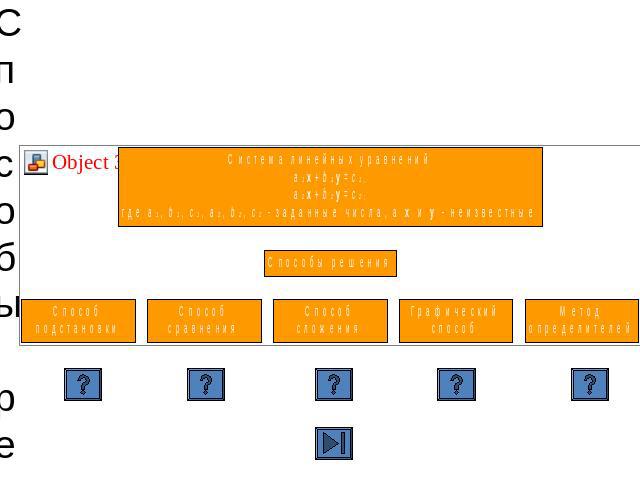
Система уравнений и её решение ОпределенияСистемой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременноКаждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системыРешением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенствоРешить систему уравнений - это значит найти все её решения или установить, что их нет

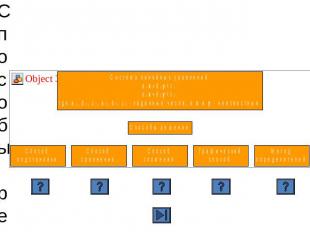
Способы решения систем уравнений

Способ подстановки (алгоритм) Из какого-либо уравнения выразить одну переменную через другуюПодставить полученное выражение для переменной в другое уравнение и решить егоСделать подстановку найденного значения переменной и вычислить значение второй переменнойЗаписать ответ: х=…; у=… .

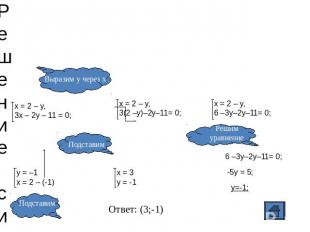
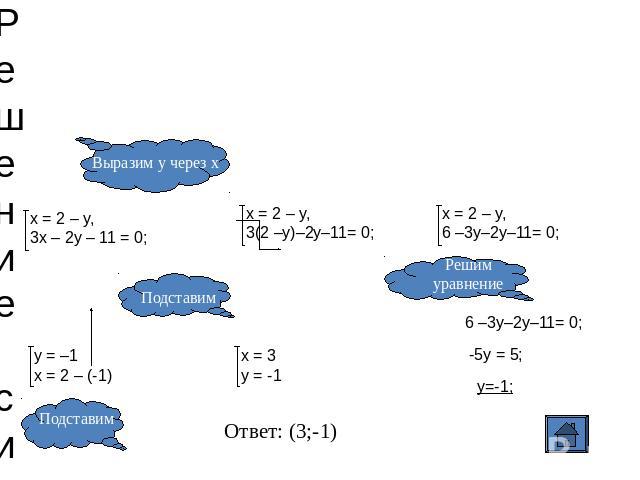
Решение системы способом подстановки Выразим у через х x = 2 – y,3x – 2y – 11 = 0; y = –1x = 2 – (-1) Подставим Подставим x = 2 – y,3(2 –y)–2y–11= 0; x = 2 – y,6 –3y–2y–11= 0; Решимуравнение 6 –3y–2y–11= 0;

Способ сравнения (алгоритм) Выразить у через х (или х через у) в каждом уравненииПриравнять выражения, полученные для одноимённых переменныхРешить полученное уравнение и найти значение одной переменнойПодставить значение найденной переменной в одно из выражений для другой переменной и найти её значениеЗаписать ответ: х=…; у=… .

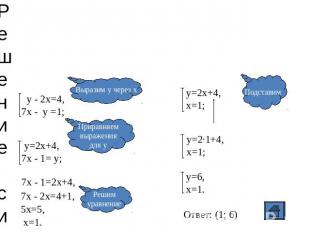
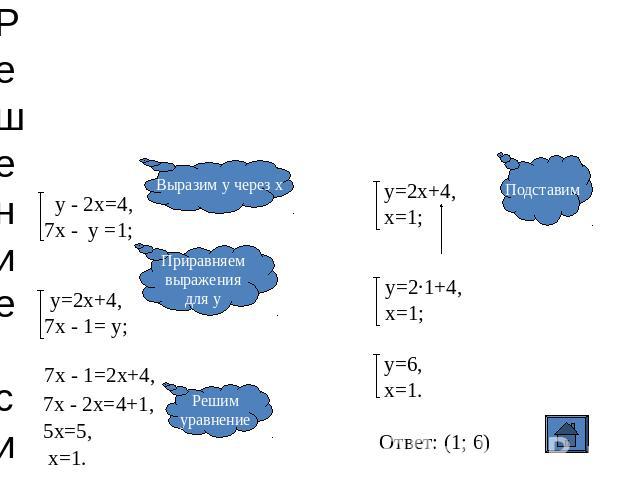
Решение системы способом сравнения у - 2х=4,7х - у =1; Выразим у через х у=2х+4,7х - 1= у; Приравняемвыражениядля у Решимуравнение 7х - 1=2х+4, 7х - 2х=4+1, Решимуравнение

Способ сложения (алгоритм) Уравнять модули коэффициентов при какой-нибудь переменнойСложить почленно уравнения системыСоставить новую систему: одно уравнение новое, другое - одно из старыхРешить новое уравнение и найти значение одной переменнойПодставить значение найденной переменной в старое уравнение и найти значение другой переменнойЗаписать ответ: х=…; у=… .

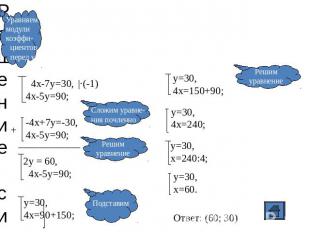
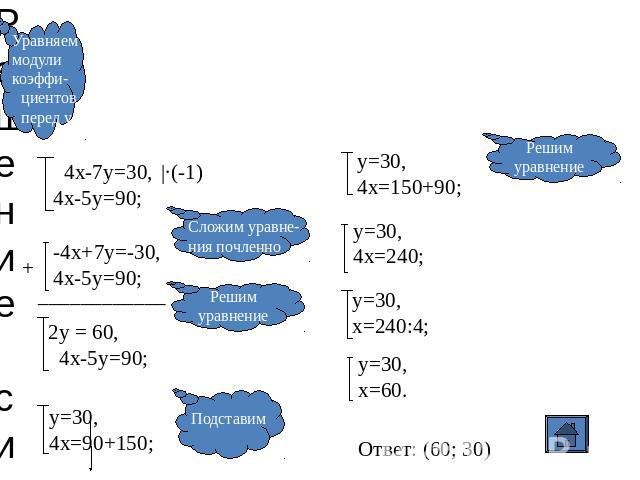
Решение системы способом сложения 4х-7у=30,4х-5у=90; -4х+7у=-30,4х-5у=90; 2y = 60, 4х-5y=90; Уравняеммодули коэффи- циентов перед у Сложим уравне-ния почленно Решимуравнение y=30,4x=150+90; y=30,4x=240; y=30,x=240:4; y=30,x=60. Решимуравнение

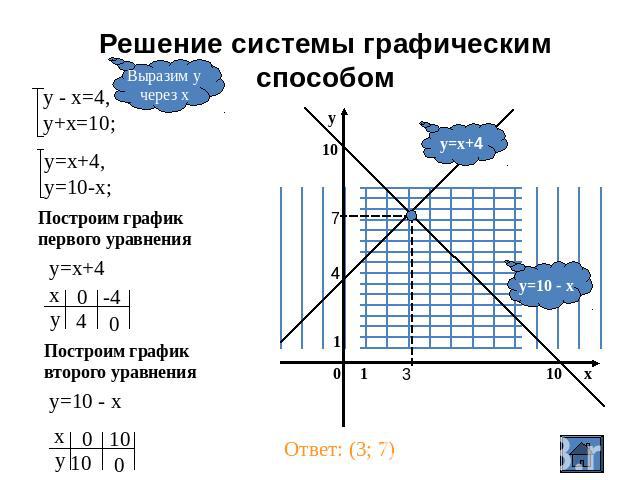
Графический способ (алгоритм) Выразить у через х в каждом уравненииПостроить в одной системе координат график каждого уравненияОпределить координаты точки пересеченияЗаписать ответ: х=…; у=… , или (х; у)

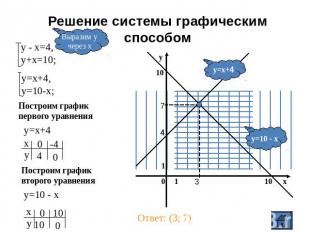
Решение системы графическим способом Выразим учерез х у - х=4,у+х=10; у=х+4,у=10-х; Построим графикпервого уравнения Построим графиквторого уравнения у=10 - х

Метод определителей (алгоритм) Составить табличку (матрицу) коэффициентов при неизвестных и вычислить определитель .Найти - определитель x, получаемый из заменой первого столбца на столбец свободных членов.Найти - определитель y, получаемый из заменой второго столбца на столбец свободных членов.Найти значение переменной х по формуле x / .Найти значение переменной у по формуле y / .Записать ответ: х=…; у=… .

Решение системы методом определителей 4х+7у=30,4х+5у=90; Составим матрицу из коэффициентовпри неизвестных = 4·5 - 7·4 = 20 – 28 = -8Составим определи- тель x, заменив в определи-теле первый столбецна столбец свободныхчленов = 30·5 - 7·90 = 150 – 630 = - 480 = 4·90 - 30·4 = 360 – 120 = 240 Найдемх и у Составим определи- тель y, заменив в определителе второй столбецна столбец свободныхчленов Ответ: х=3; у= -10 или (3;-10)

Системы рациональных уравнений Рациональным уравнением с двумя переменными х и у называют уравнения вида р(х, у) = 0, где р(х, у) – рациональное выражение.Системы рациональных уравнений, изучаемые в 9-ом классе, так же можно решать выше предложенными способами.

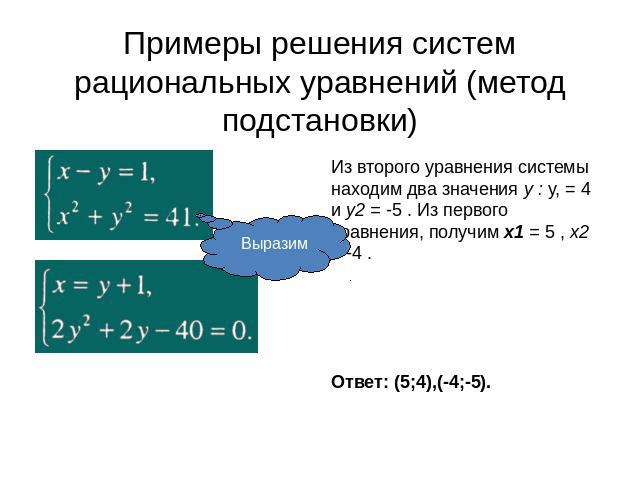
Примеры решения систем рациональных уравнений (метод подстановки) Из второго уравнения системы находим два значения у : у, = 4 и у2 = -5 . Из первого уравнения, получим х1 = 5 , х2 = -4 . Ответ: (5;4),(-4;-5).

Алгоритм метода введения новой переменной Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми.Реши полученную систему уравнений методом, наиболее подходящим для этой системы уравнений.Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.

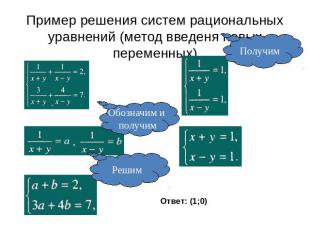
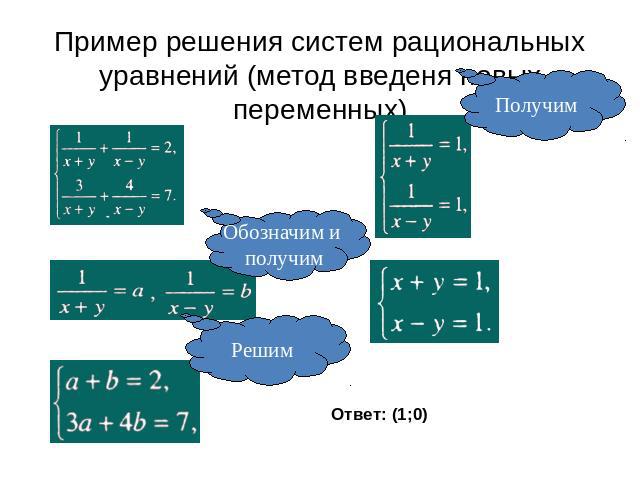
Пример решения систем рациональных уравнений (метод введеня новых переменных)Получим Обозначим и получим Решим Ответ: (1;0)

Возвратные уравнения Уравнение вида anxn+an–1xn–1 +…+a1x+a0=0называется возвратным,если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an – 1 = ak, при k = 0, 1, …, n.

Симметрические системы уравнений Система с n неизвестными называется симметрической, если она не меняется при перестановки неизвестных.Симметрическая система двух уравнений с двумя неизвестными х и у решается подстановкой u = х + у , v = ху (Заметим, что встречающиеся выражения в симметрических системах выражаются через u и v).

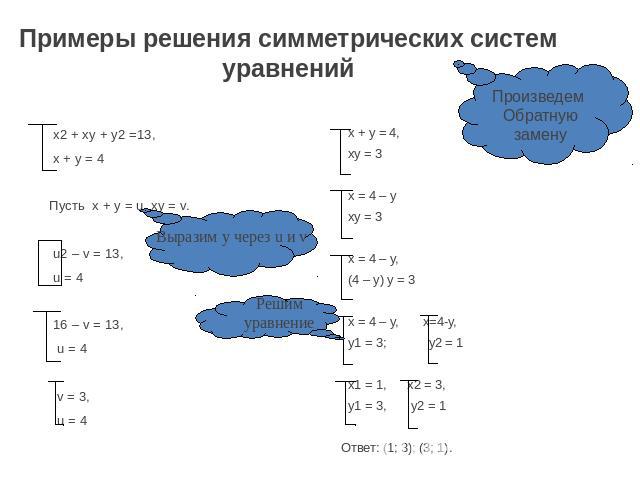
Примеры решения симметрических систем уравнений х2 + ху + у2 =13, х + у = 4Пусть х + у = u, ху = v. u2 – v = 13, u = 4 16 – v = 13, u = 4 v = 3, u = 4 Выразим у через u и v Решимуравнение х + у = 4, ху = 3 х = 4 – у ху = 3 х = 4 – у, (4 – у) у = 3 х = 4 – у, x=4-y, у1 = 3; у2 = 1 х1 = 1, х2 = 3, у1 = 3, у2 = 1Ответ: (1; 3); (3; 1). Произведем Обратнуюзамену

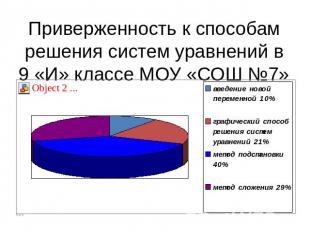
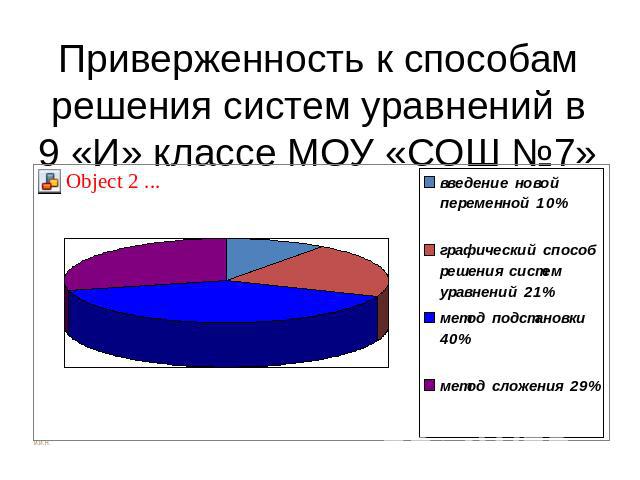
Приверженность к способам решения систем уравнений в 9 «И» классе МОУ «СОШ №7»

.Заключение В процессе написания работы мы:проанализировали и познакомились с разными видами систем алгебраических уравнений. обобщили научные сведения по теме «Системы уравнений».разобрались и научились решать системы рациональных уравнений способом введения новых переменных.рассмотрели основную теорию, связанную с симметрическими системами уравнений. научились решать симметрические системы уравнений.(Большое спасибо!)