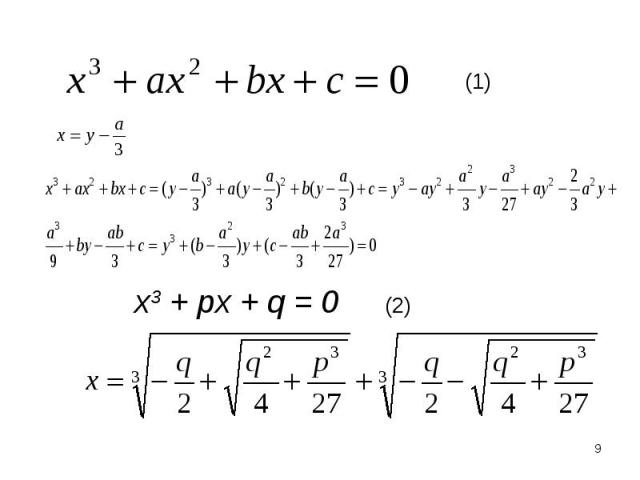Презентация на тему: Решение уравнений третьей степени

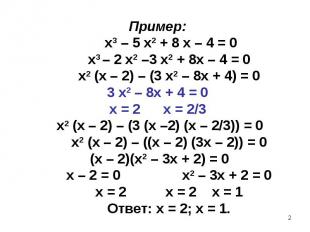
В 1543 году Кардано и Феррари поехали в Болонью, где дела Наве позволил им познакомиться с бумагами покойного дель Ферро. Там они убедились, что последнему уже было известно правило Тартальи. В 1543 году Кардано и Феррари поехали в Болонью, где дела Наве позволил им познакомиться с бумагами покойного дель Ферро. Там они убедились, что последнему уже было известно правило Тартальи. К 1543 году Кардано научился решать не только уравнения (1) и (2), но и уравнения х3 + b = ax (3) , а также «полное» кубическое уравнение, т.е. уравнение, содержащие член с х2. К тому же времени Феррари придумал, как решать уравнения четвертой степени.

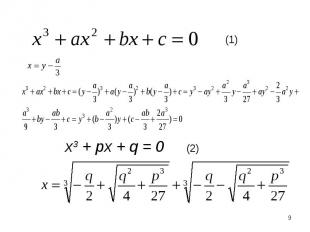
у = ах2 + bх + с (1) ( ).

Корень квадратного трехчлена является его точкой экстремума тогда и только тогда, когда этот корень – двукратный. Корень квадратного трехчлена является его точкой экстремума тогда и только тогда, когда этот корень – двукратный.

Теорема 1. Теорема 1. Для того, чтобы точка х= была точкой экстремума функции у = ах2+bх +с, необходимо и достаточно, чтобы существовало такое число m, при котором многочлен ах2+ bх + с– m имеет двукратный корень х = .

Лемма. Пусть дан многочлен третьей степени у = ах3 + bx2 + сх + d. ( ), и пусть х = - его действительный корень. Тогда у = ах3 + bx2 + сх + d = Лемма. Пусть дан многочлен третьей степени у = ах3 + bx2 + сх + d. ( ), и пусть х = - его действительный корень. Тогда у = ах3 + bx2 + сх + d = =а(х - )( , (3) где p и q – некоторые действительные числа.

Теорема 2. Теорема 2. Для того чтобы точка х = была точкой экстремума функции у = ах3 + bx2 + сх + d, необходимо и достаточно, чтобы существовало такое число m, при котором многочлен P(x) = ах3 + bx2 + сх + d – m имеет двукратный корень х = , то есть P(x)= a (4) где .

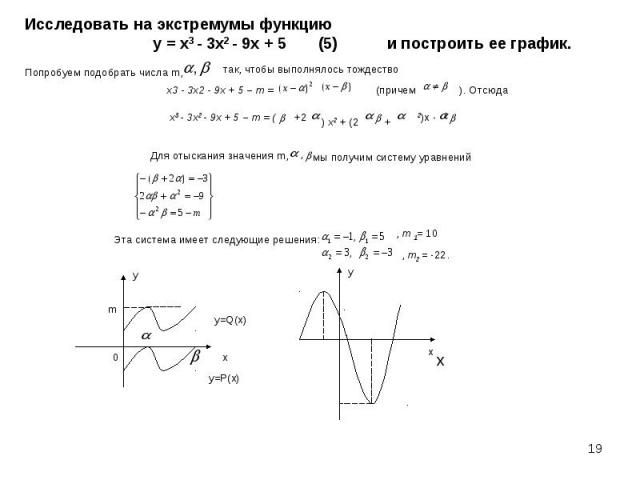
Теорема 3.(достаточные условия максимума и минимума). Теорема 3.(достаточные условия максимума и минимума). Пусть функция у = ах3 + bx2 + сх + d имеет экстремум в точке х = и m – значение функции в точке х = . Представим многочлен P(x) = ах3 + bx2 + сх + d – m в виде (4). Тогда, если >0, то х = - точка максимума; если <0, то х = - точка минимума.

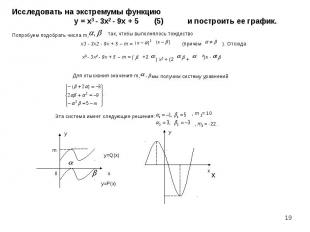
В процессе работы мы познакомились с историей развития проблемы решения уравнения третьей степени. В процессе работы мы познакомились с историей развития проблемы решения уравнения третьей степени. Теоретическая значимость полученных результатов заключается в том, что осознано место формулы Кардано в решении некоторых уравнений третьей степени. Мы убедились в том, что формула решения уравнений третьей степени существует, но она не популярна из-за ее громоздкости и не очень надежна, т.к. не всегда достигает конечного результата. Т.к. очень часто приходиться исследовать на экстремумы функции в правой части которой многочлен третьей степени, то большое практическое значение имеет алгоритм нахождения экстремумов многочлена третьей степени, который рассмотрен в работе.

В дальнейшем можно рассматривать такие вопросы: В дальнейшем можно рассматривать такие вопросы: как узнать заранее, какие корни имеет уравнение третьей степени, можно ли кубическое уравнение решить графическим способом, если можно, то как; как оценить приближенно корни кубического уравнения; как построить график кубического четырехчленна.