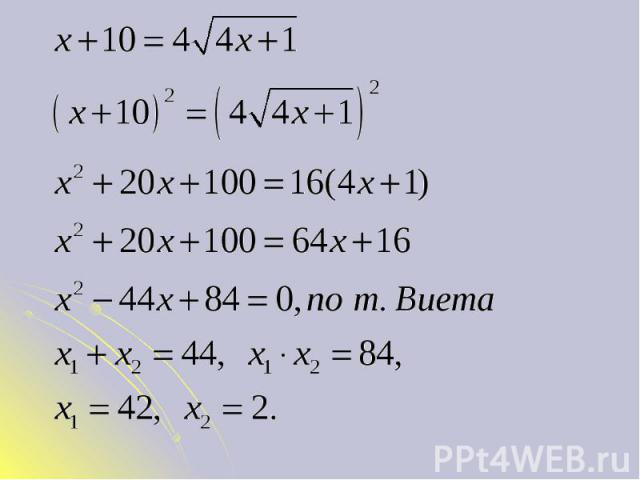Презентация на тему: Иррациональные уравнения

Ввести понятие иррациональных уравнений и показать способы их решений. Ввести понятие иррациональных уравнений и показать способы их решений. Развивать умение выделять главное, существенное в изучаемом материале, обобщать факты и понятия, развивать самостоятельность, мышление, познавательный интерес. Содействовать формированию мировоззренческих понятий.

Упростить выражение: Упростить выражение:

Решите уравнения: Решите уравнения: а) б) в) г) д)

Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень. Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

Какие из следующих уравнений являются иррациональными? Какие из следующих уравнений являются иррациональными? а) х + √ х = 2 б) х + √ х = 0 в) х √7 = 11+х г) у² - 3 √ 2 = 4 д) у + √ у²+9 = 2 е ) √ х – 1 = 3

Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же чётную степень, расширение области определения и др. Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же чётную степень, расширение области определения и др. По этим причинам необходимой частью решения иррационального уравнения является проверка, либо использование области определения заданного уравнения.

Преобразовать обе части уравнения к виду Преобразовать обе части уравнения к виду 2. Возвести обе части в n-ую степень 3. Учитывая, что получаем: 4. Решить полученное уравнение и выполнить проверку (или ОДЗ)

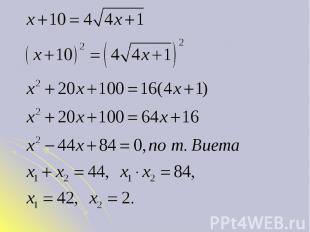
Ввести новую переменную Ввести новую переменную Решить уравнение, отбросить посторонние корни Вернуться к первоначальному неизвестному

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

В некоторых случаях можно сделать вывод о решении иррационального уравнения, не прибегая к преобразованиям. В некоторых случаях можно сделать вывод о решении иррационального уравнения, не прибегая к преобразованиям. Например, уравнения не имеют решения.

Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число входит в множество значений, то уравнение имеет единственное решение.” Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число входит в множество значений, то уравнение имеет единственное решение.” Для реализации метода, основанного на этом утверждении требуется: Выделить функцию, которая фигурирует в уравнении. Записать область определения данной функции. Доказать ее монотонность в области определения. Угадать корень уравнения. Обосновать, что других корней нет. Записать ответ.

№ 417 (а, б), № 417 (а, б), 418 (а, б), № 419 (а, б), 422 (а, б)

п. 33 п. 33 № 417 (в, г), 418 (в, г) № 419 (в, г), 422 (в, г)