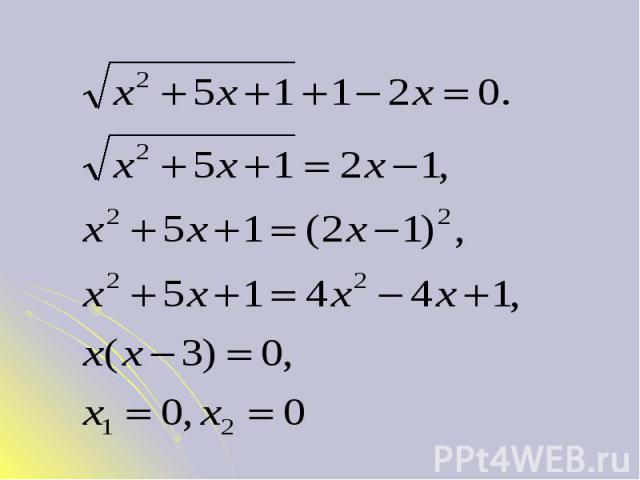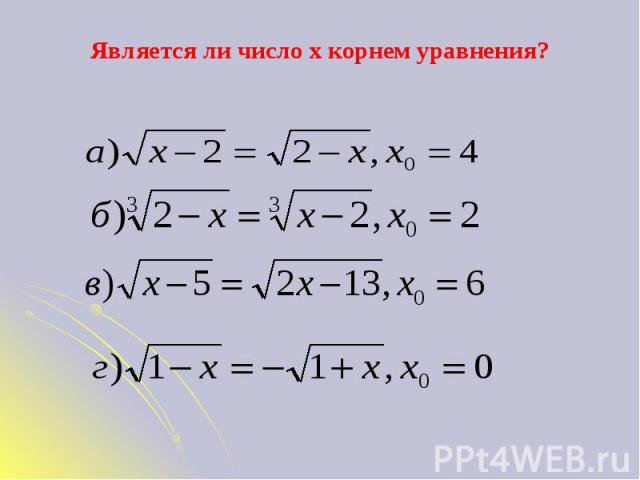Презентация на тему: Иррациональные уравнения 11 класс

Иррациональные уравнения Урок алгебры и начал анализа11 классПреподаватель: Фардиева Л. Р.

Цели урока Ввести понятие иррациональных уравнений и показать способы их решения;Выработать умение мыслить, делать выводы, применять теоретические знания для решения задач; развивать самостоятельность, мышление, познавательный интерес;Воспитание устойчивого интереса к математике, культуры поведения и общения, трудолюбия, аккуратности, положительного отношения к окружающим.

Устная работа Сколько корней имеет уравнения:а) б) в)

Найди ошибки

Тема урока Иррациональные уравнения

Определение Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.

При возведении обеих частей уравнения • в четную степень (показатель корня – четное число) – возможно появление постороннего корня (проверка необходима). • в нечетную степень (показатель корня – нечетное число) – получается уравнение, равносильное исходному (проверка не нужна).Решая иррациональные уравнения с помощью равносильных преобразований – проверка не нужна.

Посторонние корни Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту же чётную степень, расширение области определения и др. По этим причинам необходимой частью решения иррационального уравнения является проверка, либо использование области определения заданного уравнения.

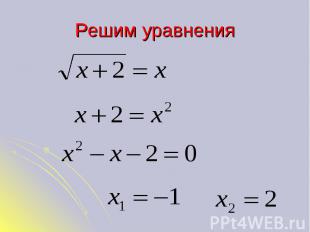
Решим уравнения

Проверка: Х = -1, тогда 1=-1 ложно;Х=2, тогда 2=2 верно.Ответ: х=2.

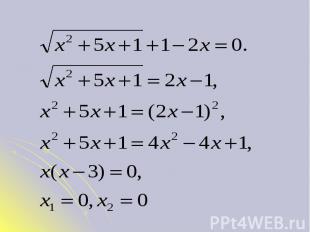
Проверка: 1) х=0, то 2) х=3, тогдаОтвет: х=3

Ответ: нет корней

Устно: Какие из следующих уравнений являются иррациональными? а) б) в) г)

Является ли число x корнем уравнения?

Решение упражнений № 417 (б, в), 418 (а, г), № 419 (в)

ДОМАШНЕЕ ЗАДАНИЕ п. 33№ 417 (г), № 419 (г)

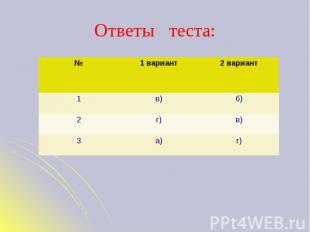
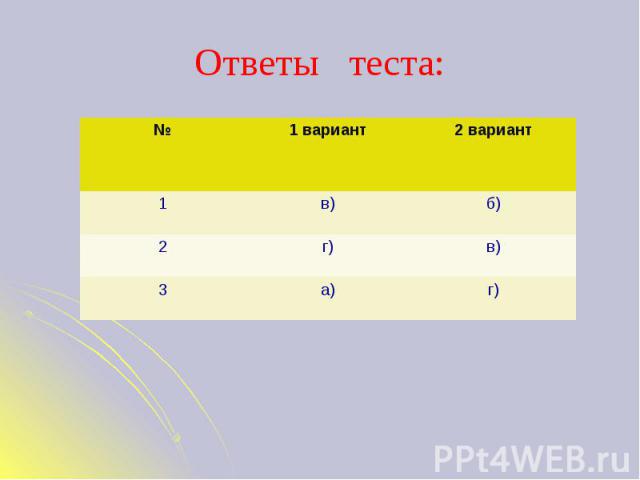
Ответы теста:

Итоги урока

Рефлексия Ваше настроение