Презентация на тему: Степенная функция

Степенная функция

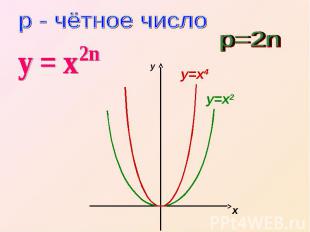
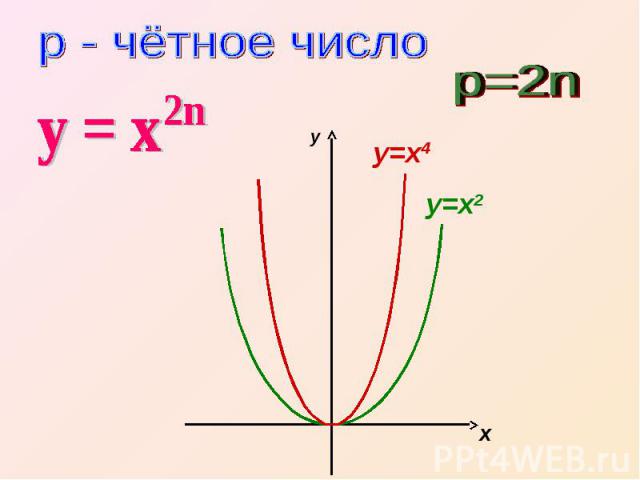
р - чётное число у = х р=2n

Свойства функции у = х— область определения — все действительные числа, т.е. множество R;— множество значений — неотрицательные числа, т. е. у ≥ 0;— функция у = х2n четная, так как (-х)2n = х2n;— функция является убываю-щей на промежутке х ≤ 0,возрастающей на промежутке х ≥ 0.

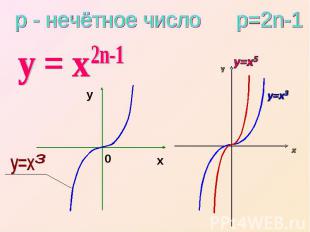
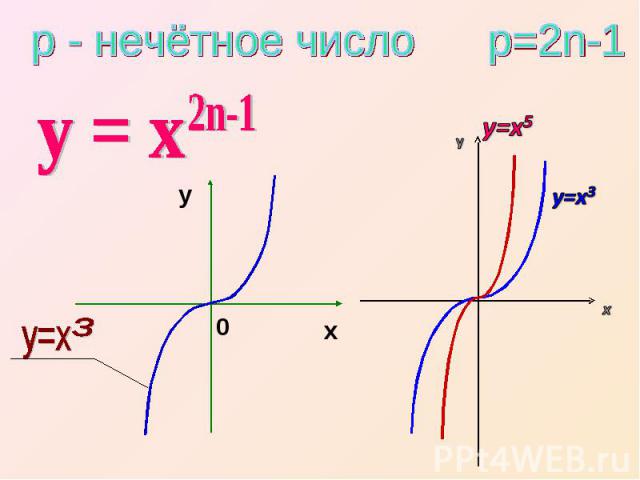
р - нечётное число р=2n-1 у = х 2n-1 y=x5

Свойства функции у = х — область определения — все действительные числа, т.е. множество R;— множество значений — все действительные числа, т.е. множество R;— функция у = х2n-1 нечетная, так как (-х)2n-1 = -х2n-1;— функция является возрастающей на промежутке х € R.

p – положительное действительное нецелое число График функции y = xр, где p – положительное нецелое число, имеет такой же вид, как, например, график функцииy = x1/3 (при 0< p

Свойства функции р – положительное действительное нецелое число. 1. Область определения: Х ≥ 02. Множество значений: У ≥ 03. Нули функции при х=04. Функция является возрастающей на промежутке X ≥ 0

p – положительное действительное нецелое Пример: График функции y = xр, где p – положительное нецелое число, имеет такой же вид, как, например, график функции y = x4/3 (при p >1).

Свойства функции 1.Область определения: x ≥ 0;2.Множество значений: y ≥ 0;3. Нули функции при х=04. Функция является возрастающей на промежутке x ≥ 0.

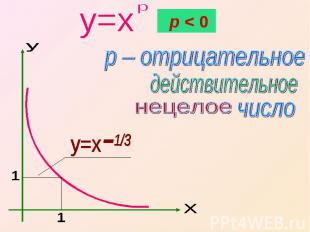
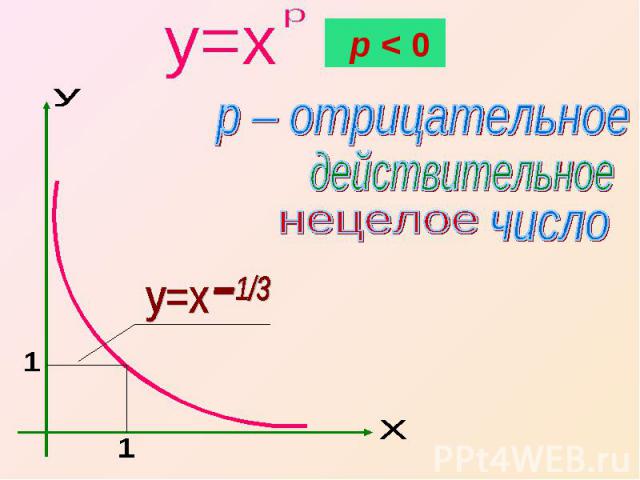
p – отрицательное действительное нецелое число

Свойства функции Область определения – положительные числа x>0;2. Множество значений – положительные числа y>0;3. Нулей нет4. Функция является убывающей на промежутке x>0.