Презентация на тему: Численные методы решения уравнений

Численные методы решения уравнений

методы Метод половинного деления Метод хорд Метод касательных Метод комбинированный Метод итераций
![Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем](https://fs1.ppt4web.ru/images/6815/78269/310/img2.jpg)
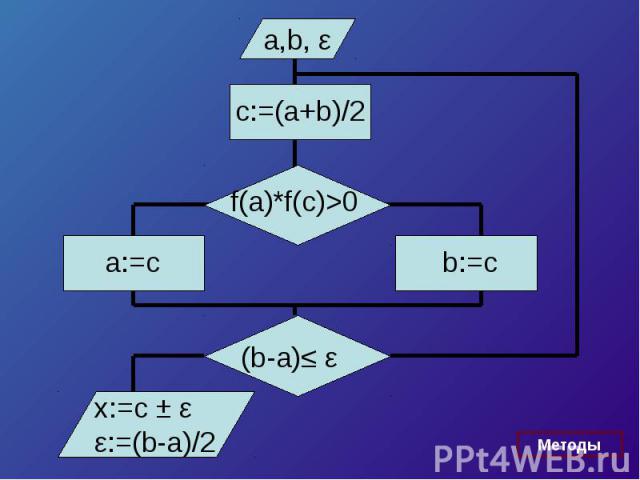
Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем считать, что функция:1)Непрерывна и монотонна на отрезке [a, b]2)f (a) x f (b) < 0 Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2 Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2
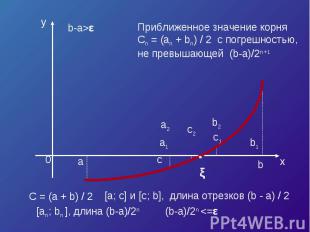
Приближенное значение корняCn = (an + bn) / 2 с погрешностью,не превышающей (b-a)/2n+1 [a; c] и [c; b], длина отрезков (b - a) / 2 [an; bn ], длина (b-a)/2n
![Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x)](https://fs1.ppt4web.ru/images/6815/78269/310/img6.jpg)
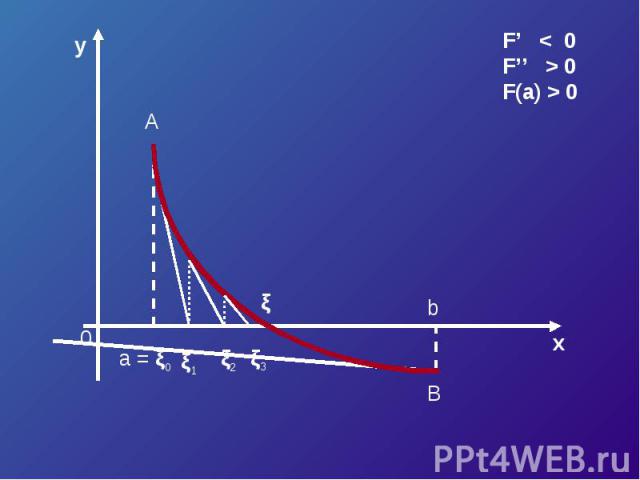
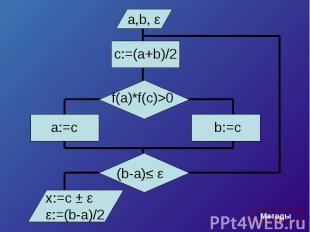
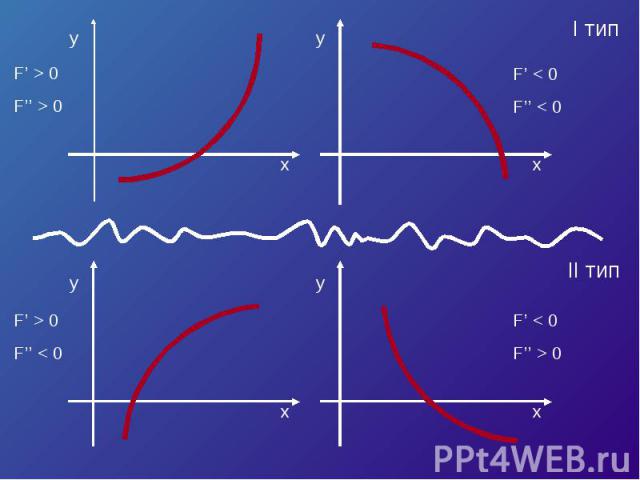
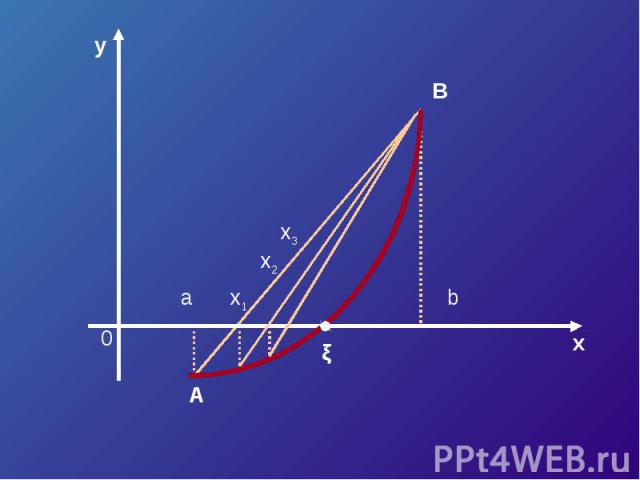
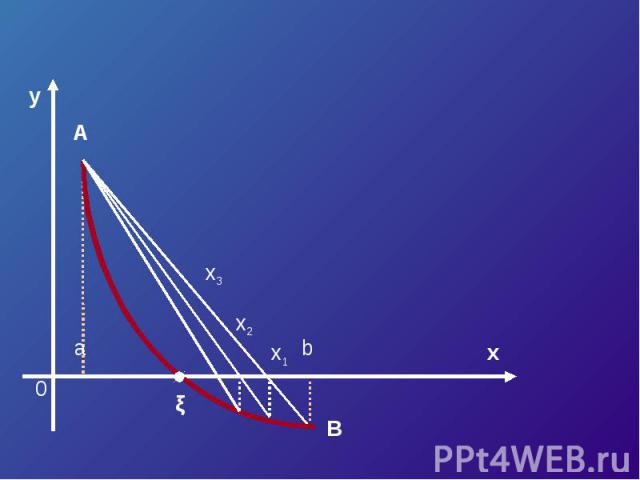
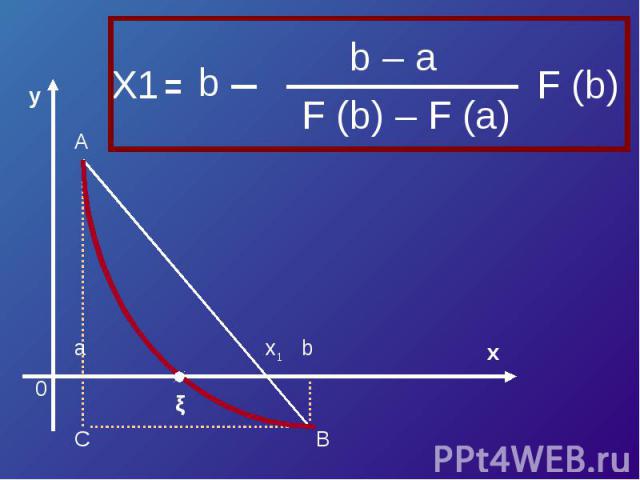
Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0
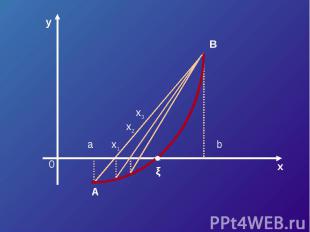
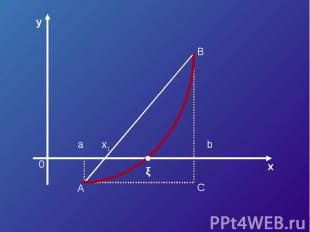

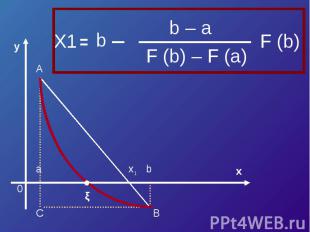
Треугольник AaX1 подобен треугольнику ABCX1 – a F (a) b – a F (a) – F (b)
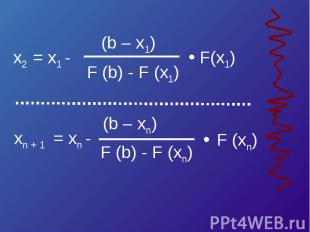
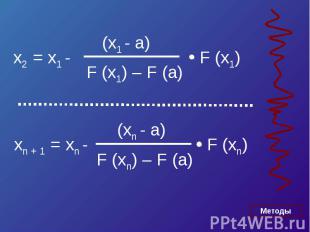
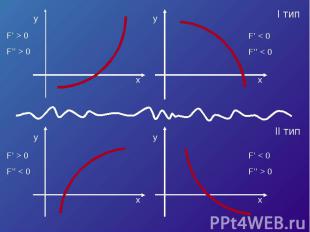
![Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x](https://fs1.ppt4web.ru/images/6815/78269/310/img15.jpg)
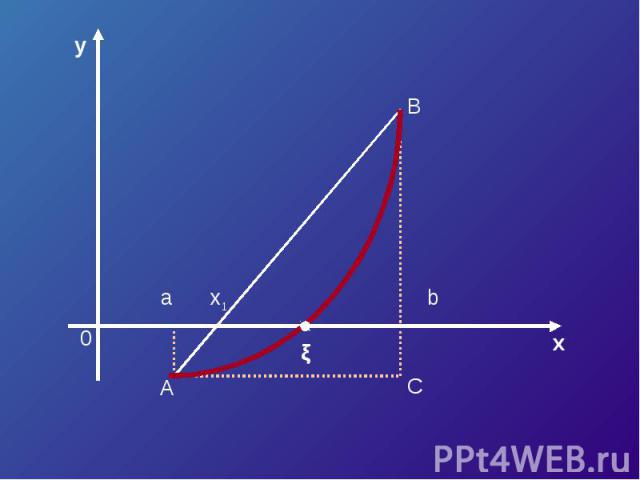
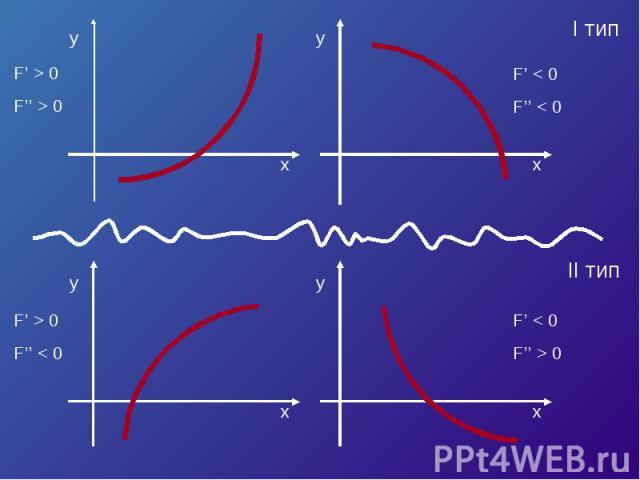
Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0
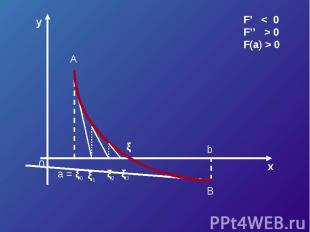
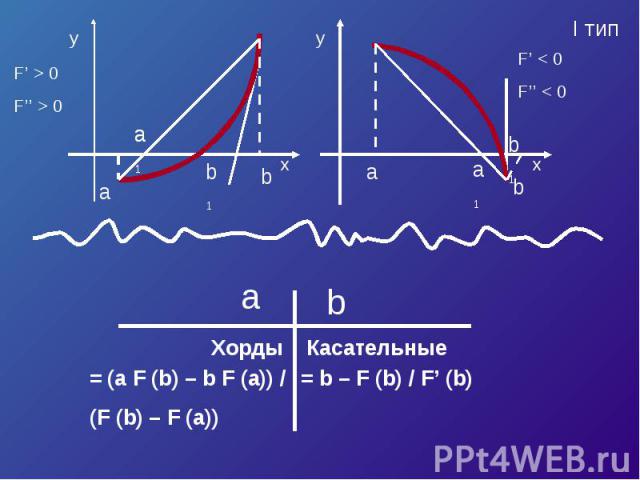
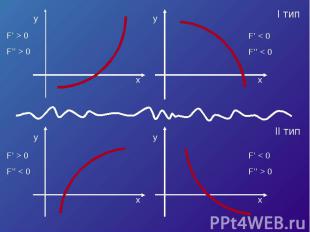
F’ < 0F’’ > 0F(a) > 0

Уравнение касательной в точке A (a, F (a)) :y – F (a) = F’ (a)*(x – a).Полагая y = 0, x = ξ 1 , получим
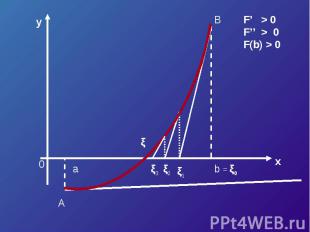
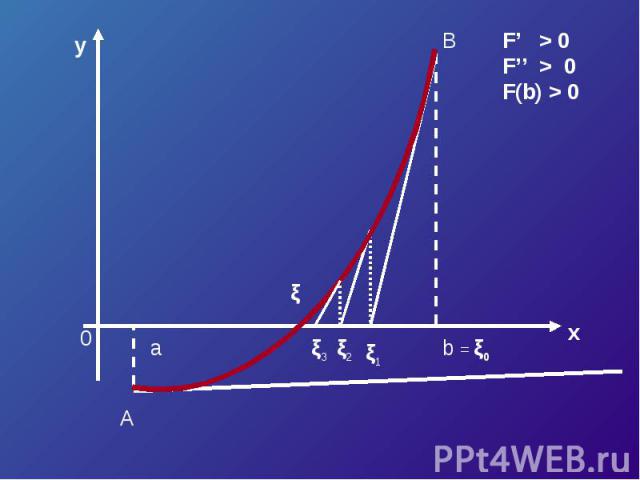
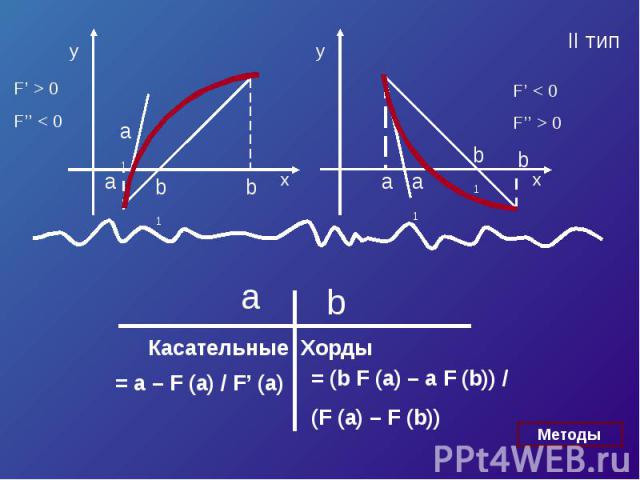
F’ > 0F’’ > 0F(b) > 0

Если касательную к кривой провести в точке B (в правом конце), то получим
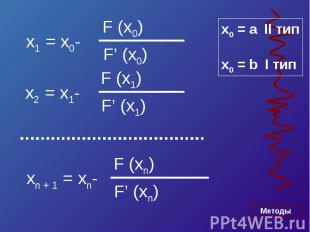
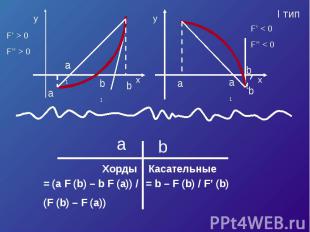
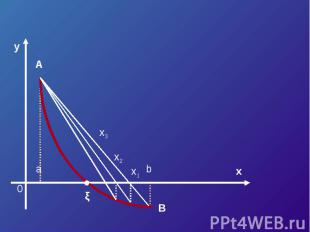
Хорды = (a F (b) – b F (a)) /(F (b) – F (a)) Касательные
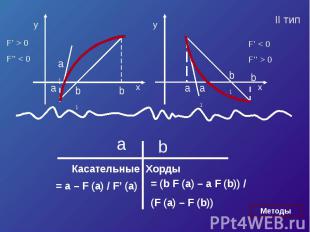
Касательные = a – F (a) / F’ (a) = (b F (a) – a F (b)) /(F (a) – F (b))






![Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем считать, что функция:1)Непрерывна и монотонна на отрезке [a, b]2)f (a) x f (b) < 0 Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2 Отрезок [a, b]… Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > ε Будем считать, что функция:1)Непрерывна и монотонна на отрезке [a, b]2)f (a) x f (b) < 0 Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2 Отрезок [a, b]…](https://fs1.ppt4web.ru/images/6815/78269/640/img2.jpg)
![Приближенное значение корняCn = (an + bn) / 2 с погрешностью,не превышающей (b-a)/2n+1 [a; c] и [c; b], длина отрезков (b - a) / 2 [an; bn ], длина (b-a)/2n Приближенное значение корняCn = (an + bn) / 2 с погрешностью,не превышающей (b-a)/2n+1 [a; c] и [c; b], длина отрезков (b - a) / 2 [an; bn ], длина (b-a)/2n](https://fs1.ppt4web.ru/images/6815/78269/640/img3.jpg)
![Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0 Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0](https://fs1.ppt4web.ru/images/6815/78269/640/img6.jpg)

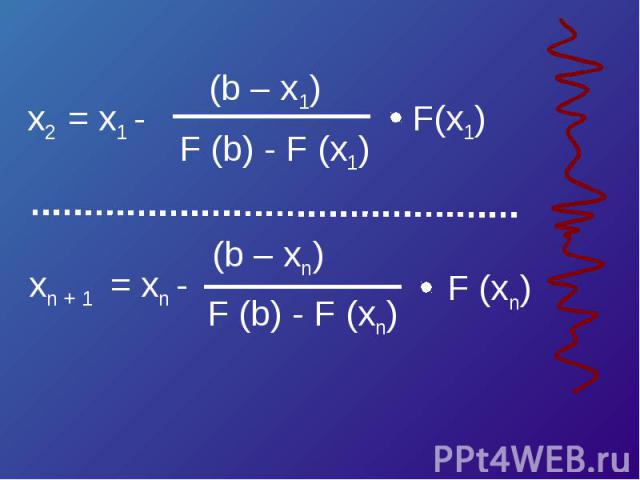

![Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0 Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b]. Будем считать:F (x) непрерывна на отрезке [a; b] F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.F (a) * F (b) < 0](https://fs1.ppt4web.ru/images/6815/78269/640/img15.jpg)