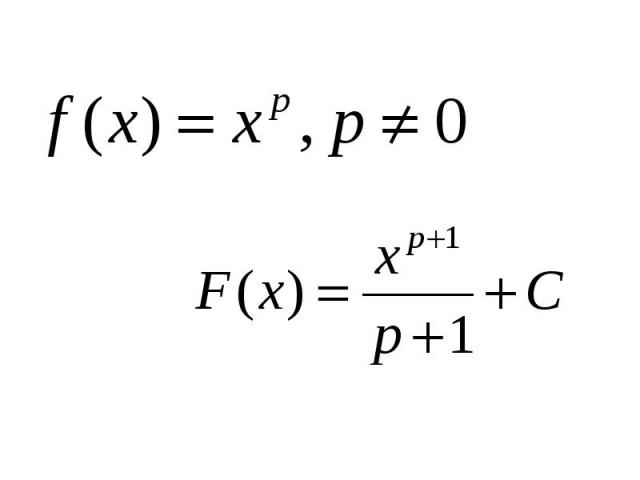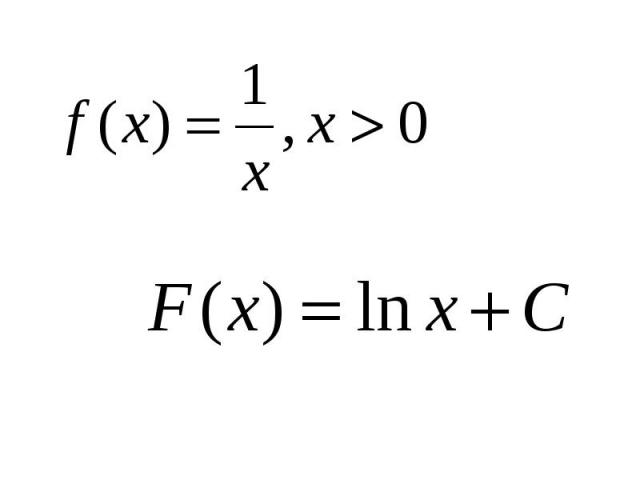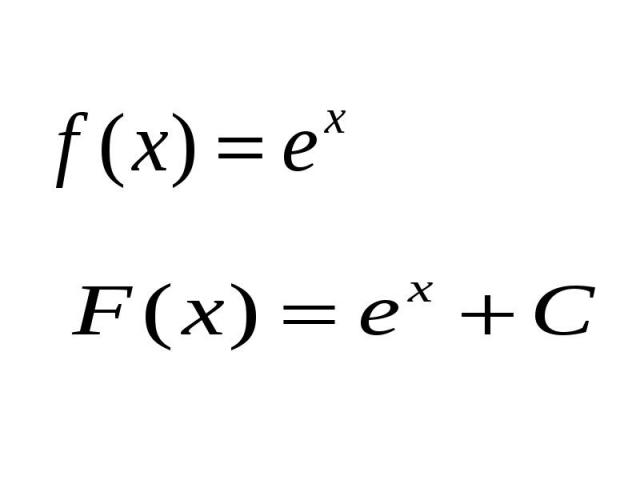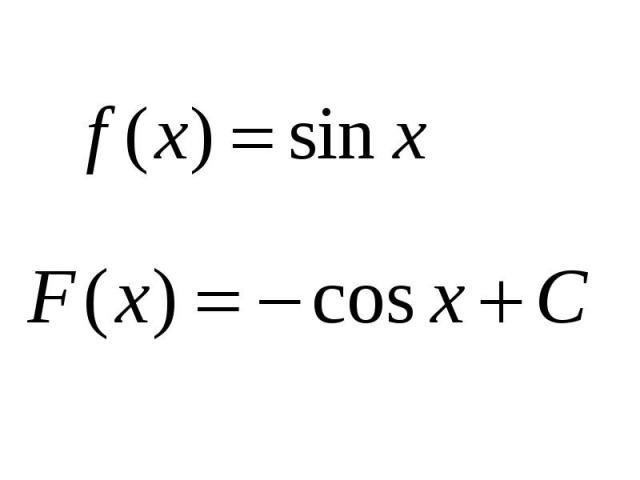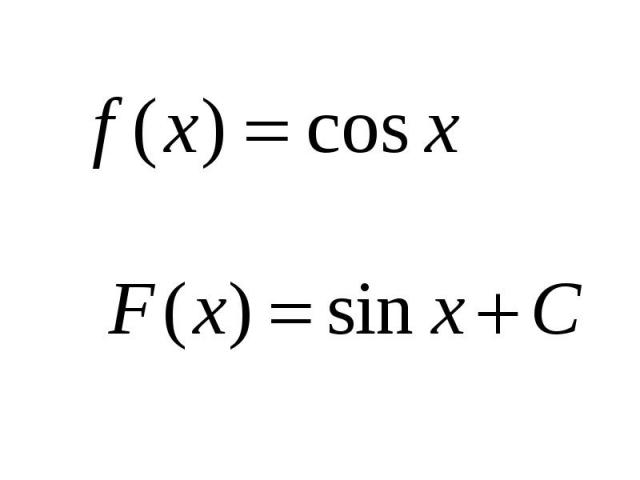Презентация на тему: Первообразная. Правила нахождения первообразных

Первообразная Правила нахождения первообразных
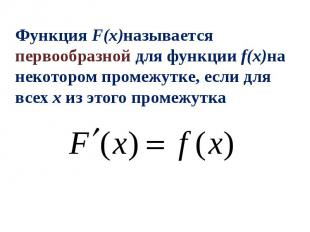
Функция F(x)называется первообразной для функции f(x)на некотором промежутке, если для всех x из этого промежутка

Показать, что функция является первообразной для функции Решение:

Показать, что функция является первообразной для функции Решение:

Если F(x)– первообразная для функции f(x) на некотором промежутке, то функция F(x)+C также является первообразной функции f(x) на этом промежутке, где C –произвольная постоянная.
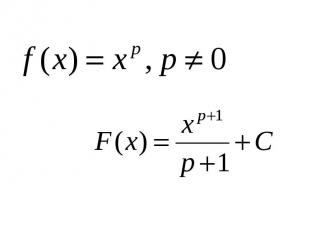
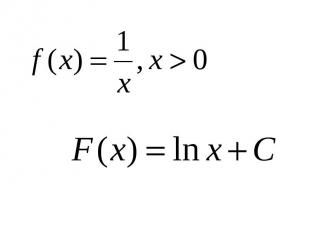
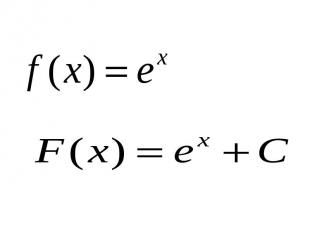
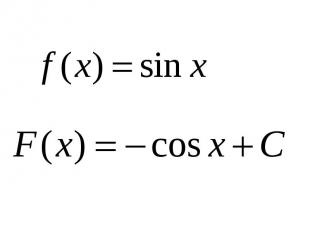
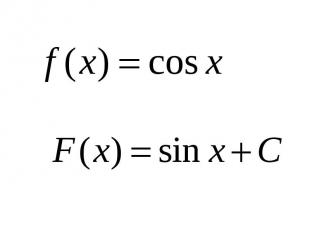

Правила нахождения первообразных

Если F(x)– первообразная для функции f(x), а G(x)– первообразная для функции g(x), то F(x)+G(x)– первообразная для функции f(x)+g(x) Первообразная суммы равна сумме первообразных

Если F(x)– первообразная для функции f(x), а а –константа, то аF(x)– первообразная для функции аf(x) Постоянный множитель можно выносить за знак первообразной

Если F(x) – первообразная для функции f(x), а k и b- константы, причем -первообразная для функции

Найти первообразные для функции Решение: