Презентация на тему: Степенная функция (11 класс)

Степенная функция Мордкович А.Г. Семенов П.В. Алгебра и начала анализа 11 классУчитель Смолькова Н.П.МОУ СОШ № 9 г. Кандалакша Мурманской обл.

Цели урока: Ввести понятие степенной функцииПостроить графики степенной функции? Сдвиг графика вдоль осей координат.-Рассмотреть свойства степенной функции в зависимости от значения показателя степени.

Как алгебраисты вместо АА, ААА, … пишут А2, А3, …так я вместо пишу а-1, а-2, а-3, … Ньютон И.

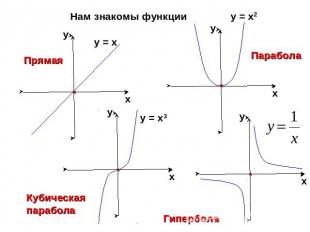
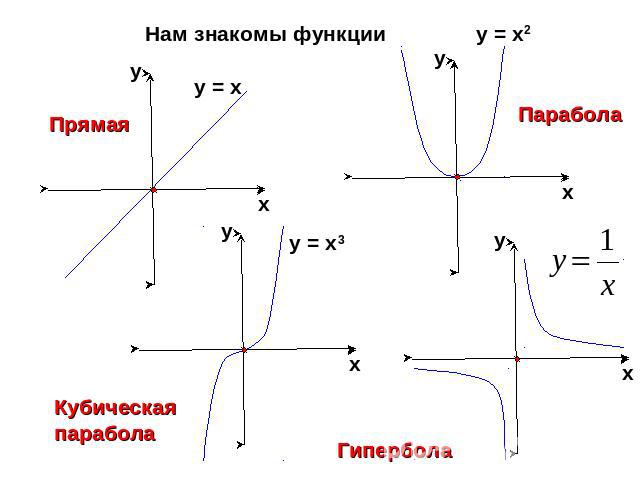
Нам знакомы функции

Все эти функции являются частными случаями степенной функции у = хr, где r – заданное действительное числоСвойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и r имеет смысл степень хr.

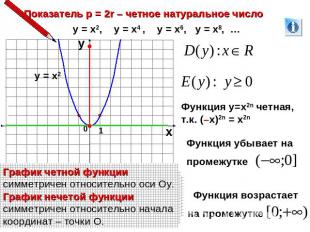
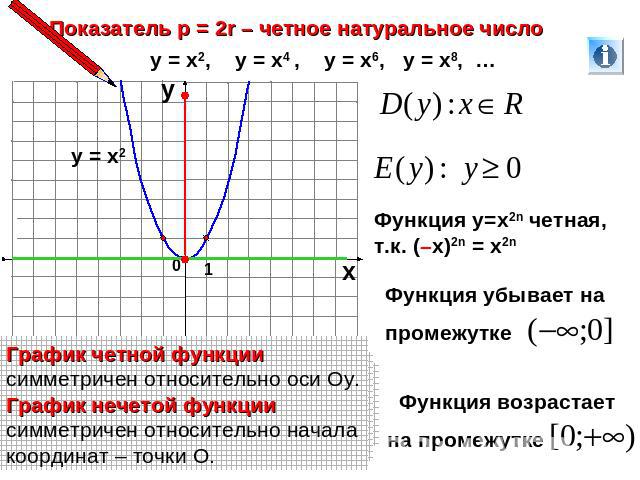
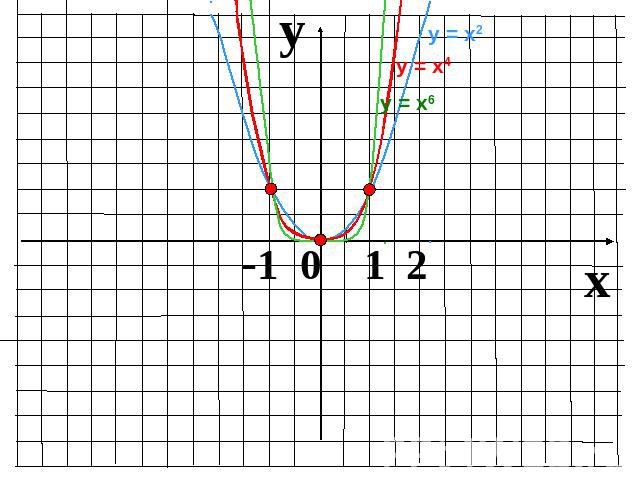
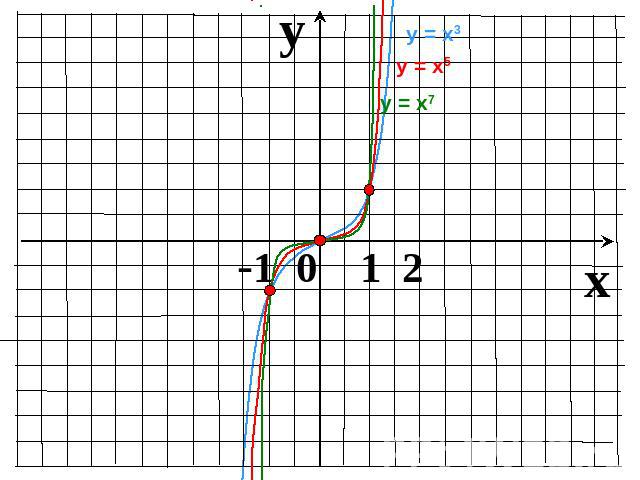
Показатель р = 2r – четное натуральное числоГрафик четной функции симметричен относительно оси Оу.График нечетой функции симметричен относительно начала координат – точки О.

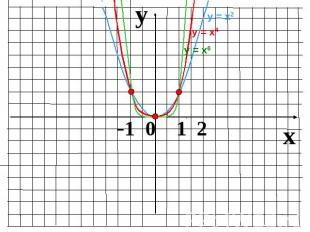
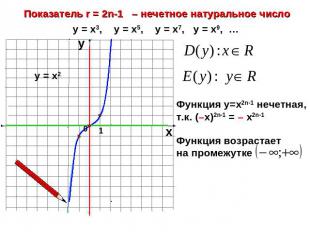
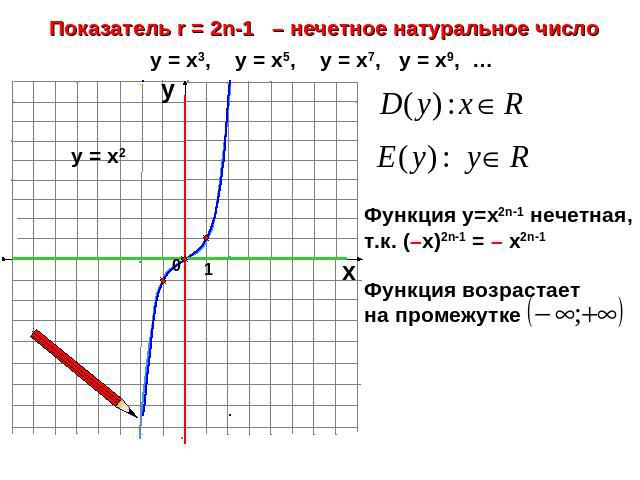
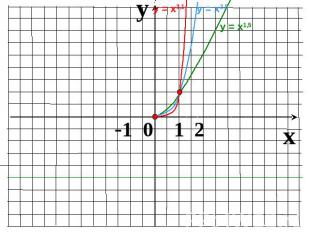
Показатель r = 2n-1 – нечетное натуральное числоФункция у=х2n-1 нечетная, т.к. (–х)2n-1 = – х2n-1Функция возрастает на промежутке

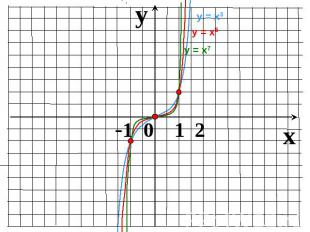
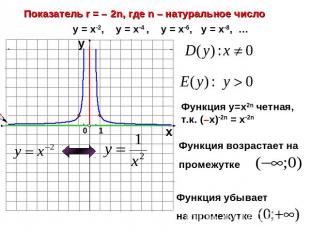
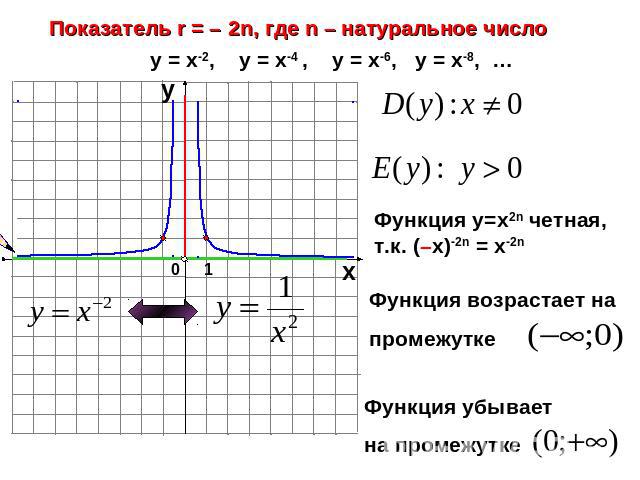
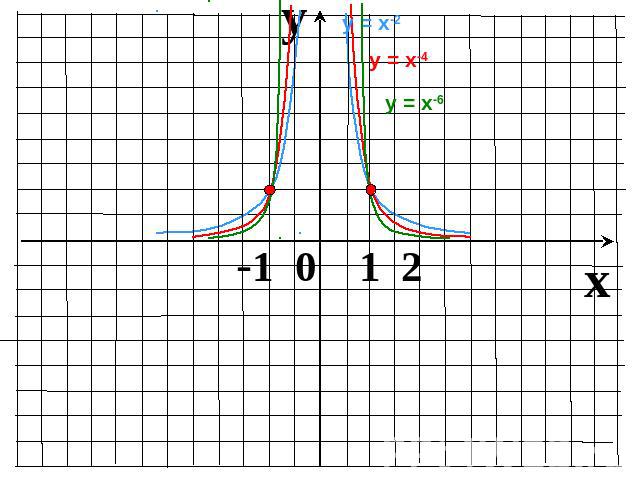
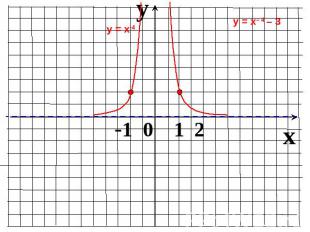
Показатель r = – 2n, где n – натуральное числоФункция у=х2n четная, т.к. (–х)-2n = х-2nФункция возрастает на промежутке Функция убывает на промежутке

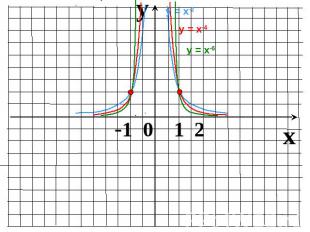
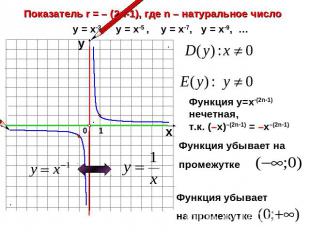
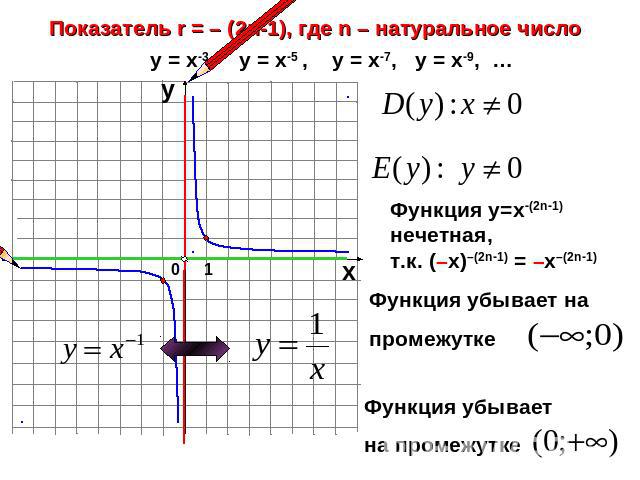
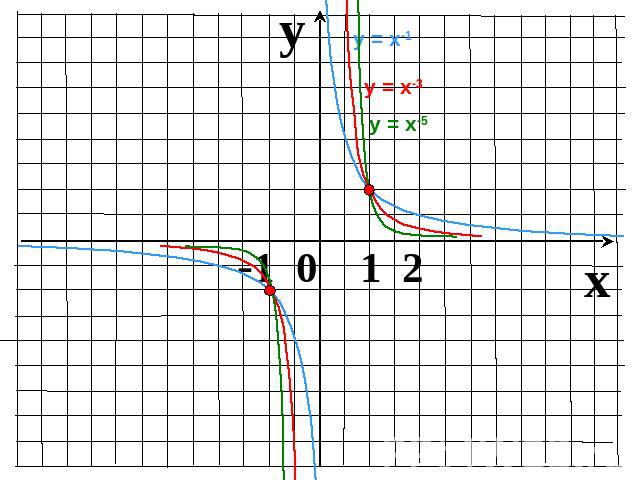
Показатель r = – (2n-1), где n – натуральное числоФункция у=х-(2n-1) нечетная, т.к. (–х)–(2n-1) = –х–(2n-1)Функция убывает на промежутке Функция убывает на промежутке

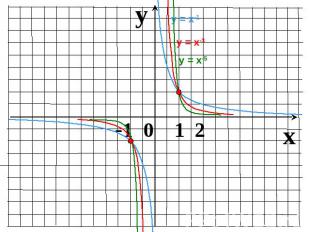
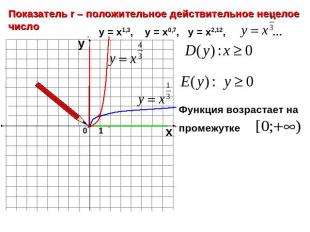
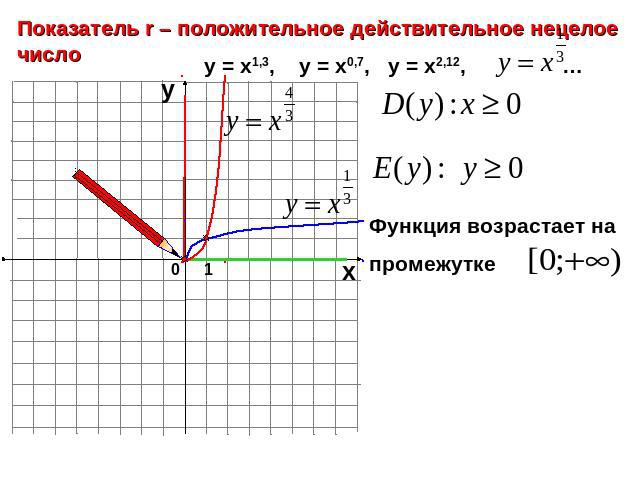
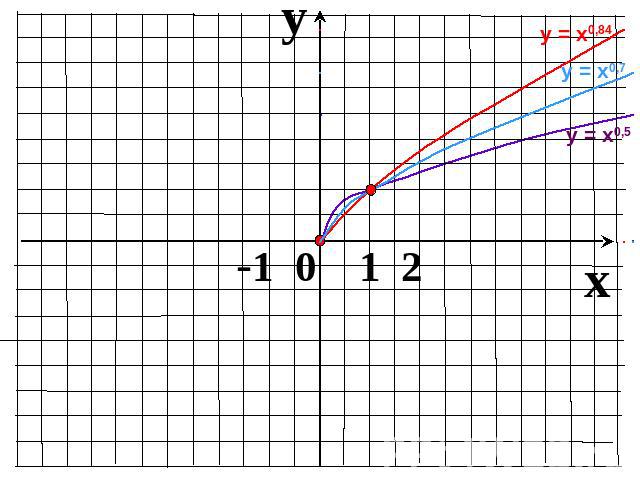
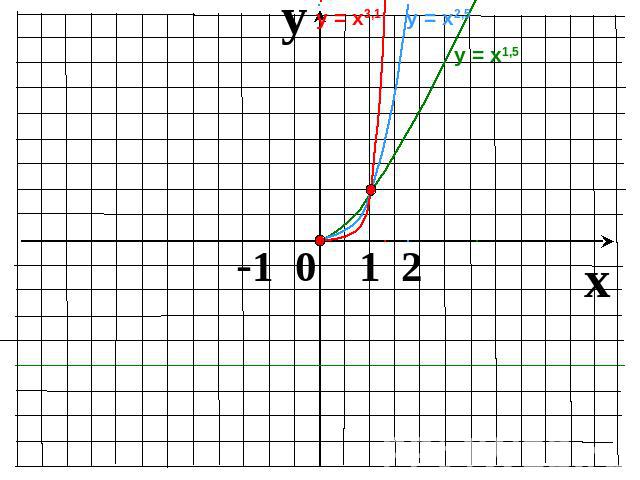
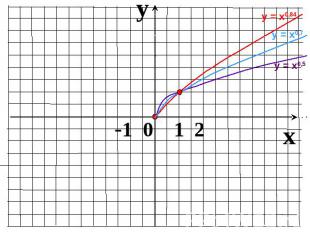
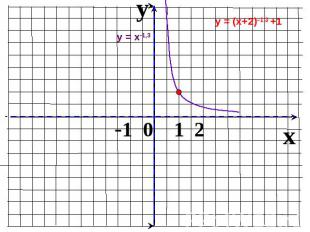
Показатель r – положительное действительное нецелое числоФункция возрастает на промежутке

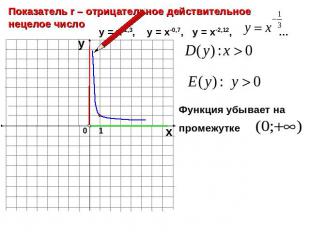
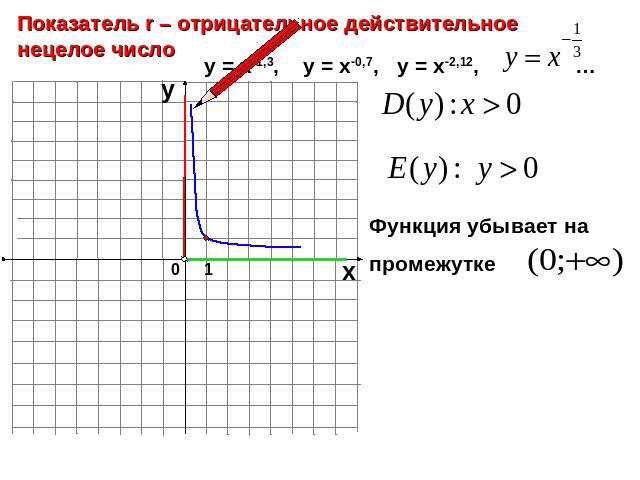
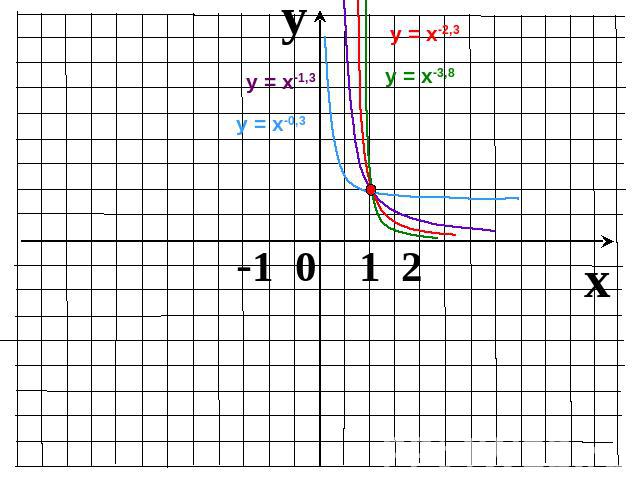
Показатель r – отрицательное действительное нецелое числоФункция убывает на промежутке

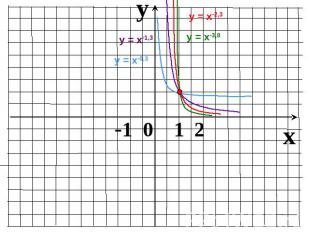
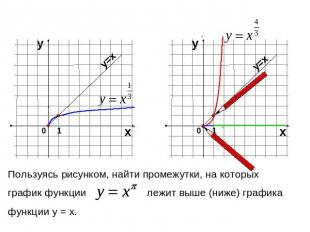
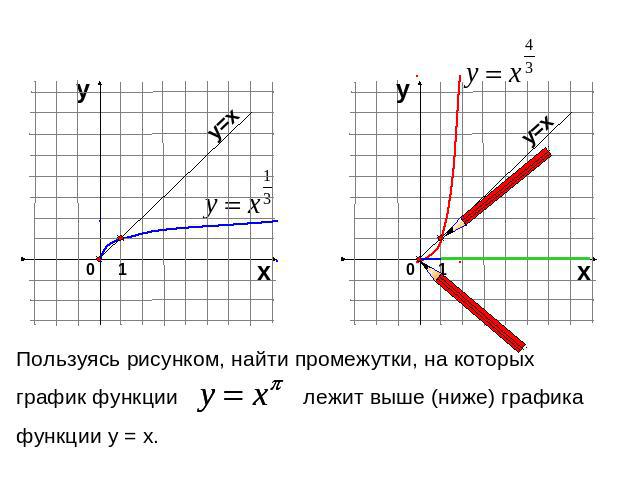
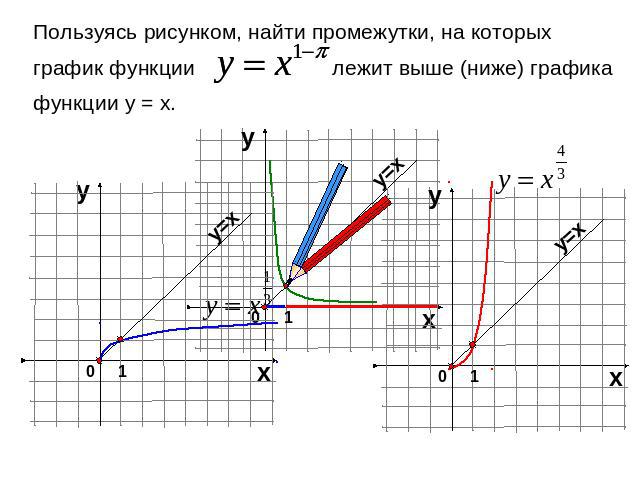
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графикафункции у = х.

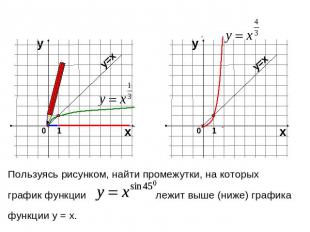
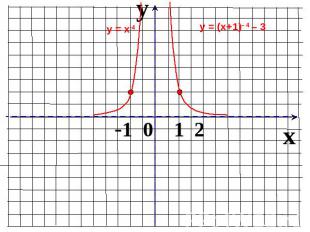
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графикафункции у = х.

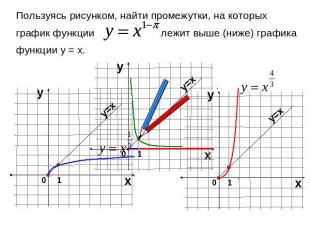
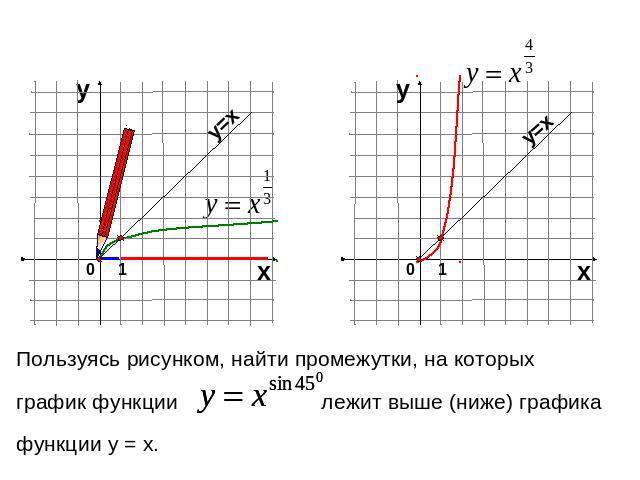
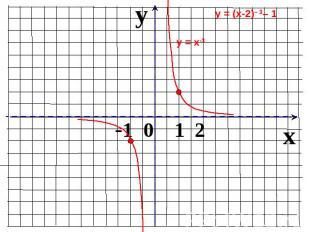
Пользуясь рисунком, найти промежутки, на которых график функции лежит выше (ниже) графика функции у = х.

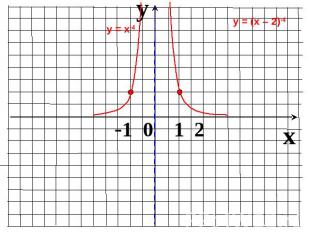
Домашнее задание 9.119.14(а,б)9.16(аб)§ 9. Определения и свойства степенной функции( стр.56-59)