Презентация на тему: Производная

Презентация на тему:Производная. Выполнили ученицы 11»а»класса:Челобитчикова Марина и Святенко Елена.Под руководством учителя математики:Плешаковой О.В. 2010 г

Содержание: 1.Из истории2.Понятие производной3.Дифференцируемость4.Замечания5.Геометрический и физический смысл производной6.Производные высших порядков7.Способы записи производных8.Примеры9.Правила дифференцирования10.Вывод11.Интернет-ресурсы

Из истории: В истории математики традиционно выделяются несколько этапов развития математических знаний:Формирование понятия геометрической фигуры и числа как идеализации реальных объектов и множеств однородных объектов. Появление счёта и измерения, которые позволили сравнивать различные числа, длины, площади и объёмы. Изобретение арифметических операций. Накопление эмпирическим путём (методом проб и ошибок) знаний о свойствах арифметических действий, о способах измерения площадей и объёмов простых фигур и тел. В этом направлении далеко продвинулись шумеро-вавилонские, китайские и индийские математики древности. Появление в древней Греции дедуктивной математической системы, показавшей, как получать новые математические истины на основе уже имеющихся. Венцом достижений древнегреческой математики стали «Начала» Евклида, игравшие роль стандарта математической строгости в течение двух тысячелетий. Математики стран ислама не только сохранили античные достижения, но и смогли осуществить их синтез с открытиями индийских математиков, которые в теории чисел продвинулись дальше греков. В XVI—XVIII веках возрождается и уходит далеко вперёд европейская математика. Её концептуальной основой в этот период являлась уверенность в том, что математические модели являются своего рода идеальным скелетом Вселенной[L 1], и поэтому открытие математических истин является одновременно открытием новых свойств реального мира. Главным успехом на этом пути стала разработка математических моделей зависимости (функция) и ускоренного движения (анализ бесконечно малых). Все естественные науки были перестроены на базе новооткрытых математических моделей, и это привело к колоссальному их прогрессу. В XIX—XX веках становится понятно, что взаимоотношение математики и реальности далеко не столь просто, как ранее казалось. Не существует общепризнанного ответа на своего рода «основной вопрос философии математики»[L 2]: найти причину «непостижимой эффективности математики в естественных науках»[L 3]. В этом, и не только в этом, отношении математики разделились на множество дискутирующих школ. Наметилось несколько опасных тенденций[L 4]: чрезмерно узкая специализация, изоляция от практических задач и др. В то же время мощь математики и её престиж, поддержанный эффективностью применения, высоки как никогда прежде

Понятие производной: Производной функции f в точке x называется число,к которому стремится разностное отношение.

Дифференцируемость Производная f'(x0) функции f в точке x0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x0 тогда и только тогда, когда её производная в этой точке существует и конечна: Для дифференцируемой в x0 функции f в окрестности U(x0) справедливо представлениеf(x) = f(x0) + f'(x0)(x − x0) + o(x − x0)

Замечания Назовём Δx = x − x0 приращением аргумента функции, а Δy = f(x0 + Δx) − f(x0) приращением значения функции в точке x0. Тогда Пусть функция имеет конечную производную в каждой точке Тогда определена производная функция Функция, имеющая конечную производную в точке, непрерывна в ней. Обратное не всегда верно. Если производная функция сама является непрерывной, то функцию f называют непрерывно дифференцируемой и пишут:

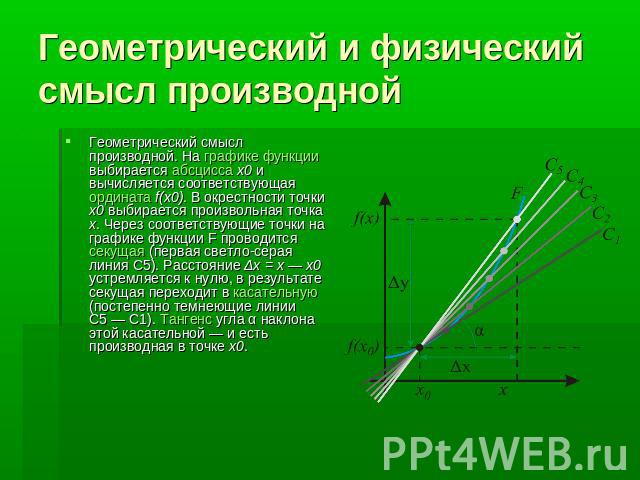
Геометрический и физический смысл производной Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.

Производные высших порядков Понятие производной произвольного порядка задаётся рекуррентно. Полагаем Если функция f дифференцируема в x0, то производная первого порядка определяется соотношением Пусть теперь производная n-го порядка f(n) определена в некоторой окрестности точки x0 и дифференцируема. Тогда

Способы записи производных В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:Лагранжа f(n)(x0), при этом для малых n часто используют штрихи и римские цифры: f(1)(x0) = f'(x0) = fI(x0),f(2)(x0) = f''(x0) = fII(x0),f(3)(x0) = f'''(x0) = fIII(x0),f(4)(x0) = fIV(x0), и т. д.Такая запись удобна своей краткостью и широко распространена;Лейбница, удобная наглядной записью отношения бесконечно малых: Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:  — производная первого порядка x по t при t = t0, или — вторая производная f по x в точке x0 и т.д.Эйлера, использующая дифференциальный оператор (строго говоря, дифференциальное выражение, пока не введено соответствующее функциональное пространство), и потому удобная в вопросах, связанных с функциональным анализом: , Конечно, при этом надо не забывать, что служат все они для обозначения одних и те же объектов:

Примеры: Пусть f(x) = x2. Тогда Пусть f(x) = | x | . Тогда если то f'(x0) = sgnx0,где sgn обозначает функцию знака. Если x0 = 0, то а следовательно f'(x0) не существует

Правила дифференцирования Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. (производная суммы равна сумме производных) (отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу) Если функция задана параметрически: то,

Вывод: Производная использовалась с глубоких времен,и применяется до сих пор,в наши дни.Производная одно из основных понятий дифференциального исчисления.

Источники информации Учебник по алгебре 10-11 класса.Автор:Колмогоров.Большая школьная энциклопедия.Автор:Штейн Е.Аhttp://ru.wikipedia.org/