Презентация на тему: Свойства функций непрерывных на отрезке

Тема урока:Свойства функций непрерывных на отрезке

Ответить на вопросы: Дайте определение монотонно возрастающей (убывающей) функции;Дайте определение функции непрерывной в точке;Дайте определение функции непрерывной на промежутке;Сформулируйте теорему Больцано-Коши (о промежуточных значениях);Сформулируйте теорему о корне.

Рассмотрим функцию и ответим на вопросы: Какова область определения этой функции?Какова ее область значений?Является ли эта функция монотонной?Каков характер ее монотонности (возрастает, убывает)?Может ли эта функция принимать значение равное 0? 1? 5? 14? Почему?При каком х значение функции f(x)=3?

Теорема Больцано-Коши: Если функция непрерывна на отрезке и на концах его принимает значения противоположных знаков, то внутри отрезка существует по крайней мере одна точка, в которой функция принимает значение равное нулю.

Задача: вычислить корень уравнения на отрезке [-1;0]

решение:

Теорема о корне: Если функция f(x) определена на множестве I и монотонно возрастает (убывает) на нем, то уравнение f(x)=a имеет единственное решение, если а принадлежит множеству значений функции f(x) и не имеет решений, если число а этому множеству не принадлежит.

Задача:решить уравнение

Решение: x =2 является корнем уравнения. Рассмотрим функцию Исходное уравнение примет вид: Функция определена на множестве [1;+∞) и монотонно возрастает на нем (как сумма возрастающих функций). По теореме о корне х =2 является единственным корнем уравнения.

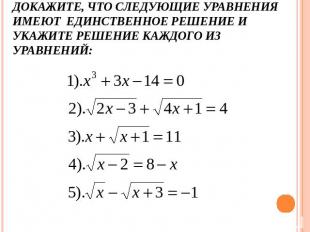
ДОКАЖИТЕ, ЧТО СЛЕДУЮЩИЕ УРАВНЕНИЯ ИМЕЮТ ЕДИНСТВЕННОЕ РЕШЕНИЕ И УКАЖИТЕ РЕШЕНИЕ КАЖДОГО ИЗ УРАВНЕНИЙ:

Докажите, что следующие уравнения не имеют решений:

Решим уравнение Это уравнение определено при х > -3. Использование определения логарифма в данном случае приводит к трудно разрешимому уравнениюПоступим иначе, введем в рассмотрение функцию Тогда исходное уравнение примет вид:Функция монотонно возрастает на (-3;+∞), поэтому уравнение имеет единственный кореньх = 2.

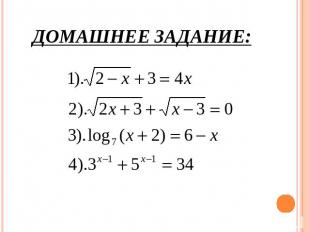
Домашнее задание: