Презентация на тему: Свойства функций

Свойства функцийУрок №1

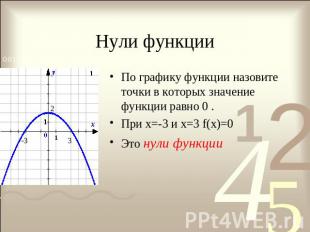
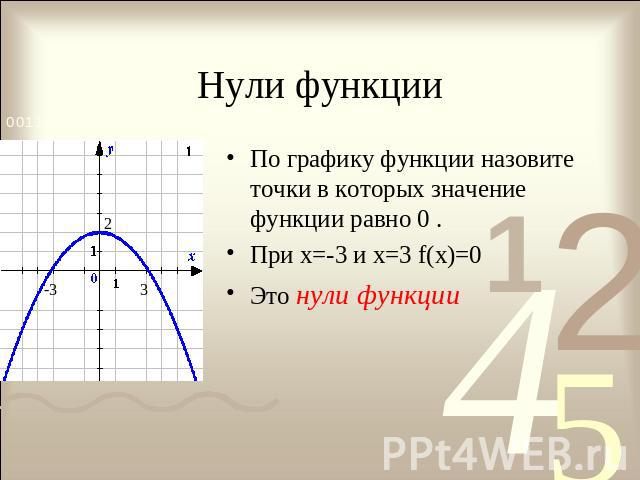
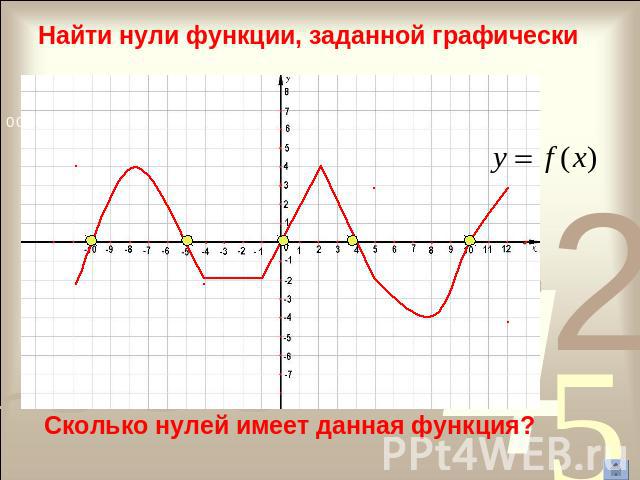
Нули функции По графику функции назовите точки в которых значение функции равно 0 .При х=-3 и х=3 f(x)=0Это нули функции

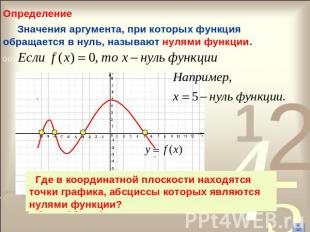
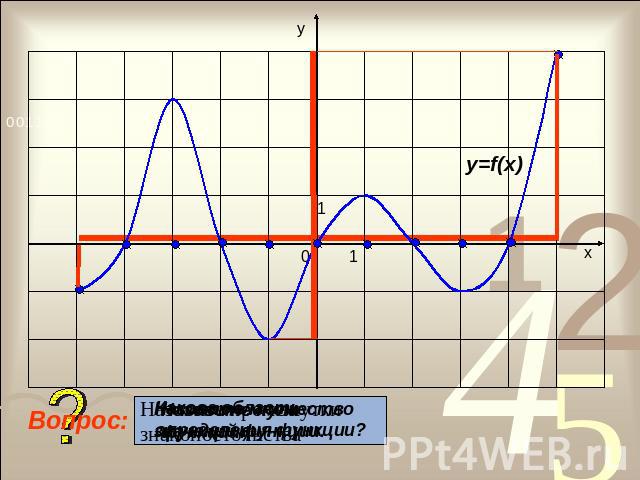
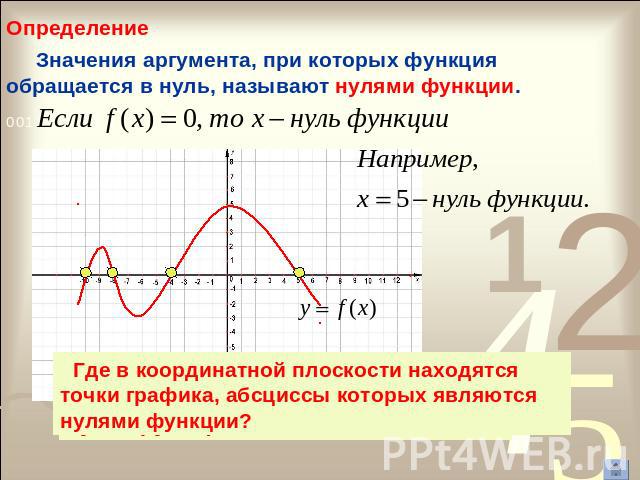
Определение Значения аргумента, при которых функция обращается в нуль, называют нулями функции. Где в координатной плоскости находятся точки графика, абсциссы которых являются нулями функции?

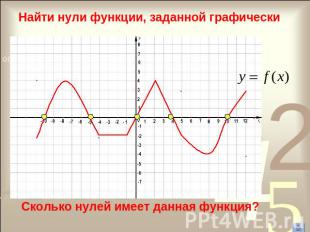
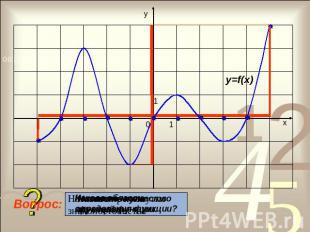
Найти нули функции, заданной графическиСколько нулей имеет данная функция?

Как найти нули функции, заданной формулой?

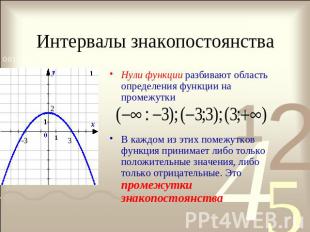
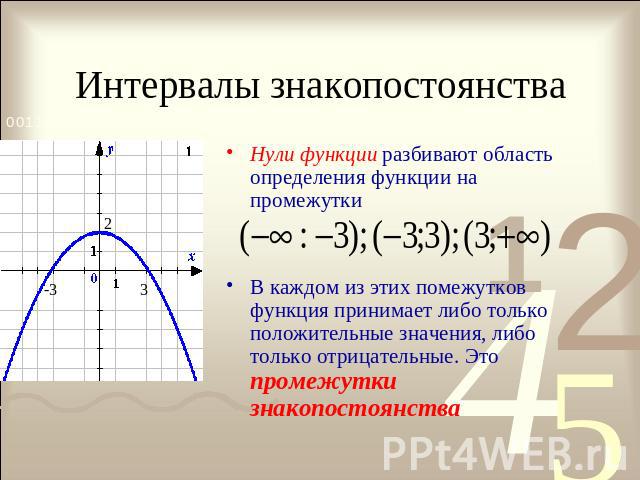
Интервалы знакопостоянства Нули функции разбивают область определения функции на промежуткиВ каждом из этих помежутков функция принимает либо только положительные значения, либо только отрицательные. Это промежутки знакопостоянства

Исследование функций на монотонностьесли двигаться по графику слева направо, то ординаты точек графика всё время увеличиваются («поднимаемся в горку»); говорят, что функция возрастает;если двигаться по графику слева направо, то ординаты точек графика всё время уменьшаются («спускаемся с горки»); говорят, что функция убывает.

ОпределениеФункция у = f (х) называют возрастающей на промежутке Х, если из неравенства х1 < х2, где х1 и х2 – любые две точки промежутка Х, следует неравенство f (х1) < f (х2). Определение 2.Функция у = f (х) называют убывающей на промежутке Х, если из неравенства х1 < х2, где х1 и х2 – любые две точки промежутка Х, следует неравенство f (х1) > f (х2).

1. Линейная функция у = kx + m. Теорема. 1. Если k > 0, то функция возрастает на всей числовой прямой.2. Если k < 0, то функция убывает на всей числовой прямой.

1. Пусть у = f (x), где f (x) = kx + m. 1) Если х1 < х2 и k > 0, то kx1 < kx2 (по свойству 3).2) Прибавим к левой и правой части неравенства число m: kx1 + m < kx2 + m (по свойству 2), т.е. f (x1) < f (x2).3) Итак, если х1 < х2 ,то f (x1) < f (x2), значит функция у = kx + m возрастает. 2. Пусть у = f (x), где f (x) = kx + m. 1) Если х1 < х2 и k < 0, то kx1 > kx2 (по свойству 3).2) Прибавим к левой и правой части неравенства число m: kx1 + m > kx2 + m (по свойству 2), т.е. f (x1) > f (x2).3) Итак, если х1 < х2 , то f (x1) > f (x2), значит функция у = kx + m убывает. Замечание. Если функция возрастает (убывает) по всей своей области определения, то её можно назвать возрастающей(убывающей), не указывая промежуток.

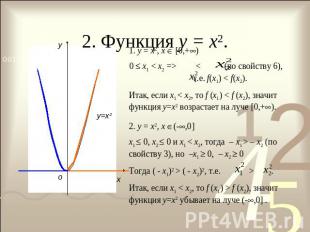
2. Функция у = х2. 1. у = х2, х [0,+)0 х1 < х2 => < (по свойству 6), т.е. f(x1) < f(x2).Итак, если х1 < х2, то f (x1) < f (x2), значит функция у=х2 возрастает на луче [0,+).2. у = х2, х (-,0]х1 0, x2 0 и х1 < х2, тогда – х1 > – х2 (по свойству 3), но –х1 0, – х2 0 Тогда ( - х1)2 > ( - х2)2, т.е. > .Итак, если х1 < х2, то f (x1) > f (x2), значит функция у=х2 убывает на луче (-,0] .

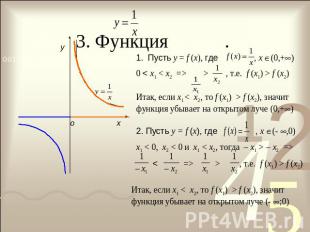
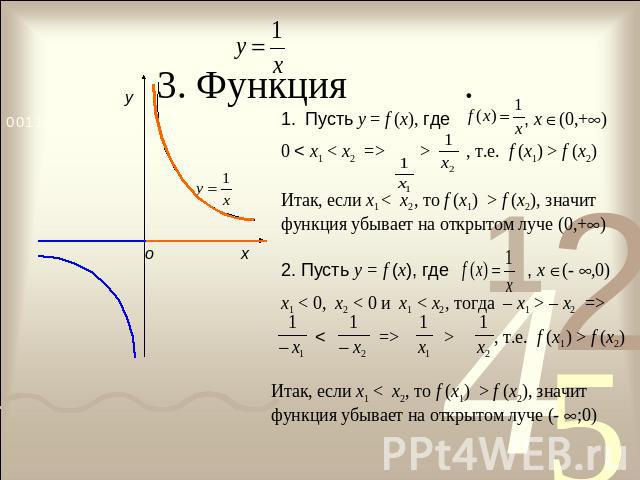
3. Функция . Пусть у = f (x), где , x (0,+) 0 < x1 < x2 => > , т.е. f (x1) > f (x2) Итак, если х1 < х2, то f (x1) > f (x2), значит функция убывает на открытом луче (0,+)2. Пусть у = f (x), где , х (- ,0)x1 < 0, x2 < 0 и x1 < x2, тогда – x1 > – x2 => < => > , т.е. f (x1) > f (x2) Итак, если х1 < х2, то f (x1) > f (x2), значит функция убывает на открытом луче (- ;0)

Свойства линейной функции у = kx + m

Свойства функции Функция убывает на промежутках (-;0) и (0;+)Функция возрастает на промежутках (-;0) и (0;+)

Свойства функции у = kx2

Упражнения №31№33(а,б)№35(а,б)№39(а,б)

Домашнее задание п 2 №30№32№36№40№41

Свойства функций Урок №2

Устно: Перечислите свойства функции:у=5х-4у=3х2;у=-2/х

Устно Представить в виде квадрата двучлена:

Упражнения №34№37

Самостоятельная работа

Домашнее задание п 2 №29№38№152№153