Презентация на тему: Свойства функций (9 класс)

Краткий электронный справочник. Свойства функций Авторы: Щербак Н. А., Морозов В. В. 9 «Б» классУчитель: Хрусталева С. И.ГОУ СОШ № 549 г. Москвы

Вступительное слово. Дорогие друзья! Мы представляем Вашему вниманию презентацию для обучения и подготовке к экзамену по алгебре. Тема нашей работы «Свойства функций». В работе представлены те функции, которые изучаются в курсе алгебры 7, 8, 9 классов. Получить дополнительную информацию вы можете по ссылке>>

Выберите тему:

Свойства функций

Примеры построения

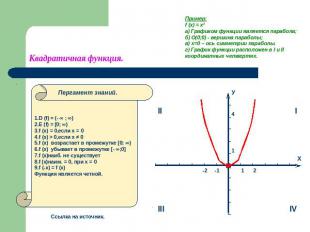
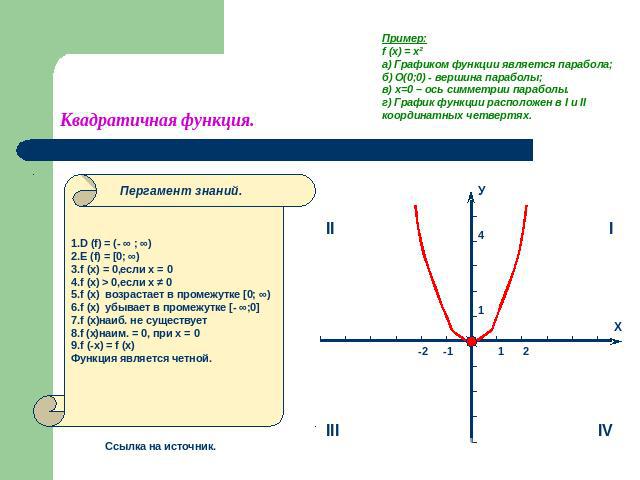
Квадратичная функция. Пример:f (x) = х²а) Графиком функции является парабола;б) О(0;0) - вершина параболы;в) х=0 – ось симметрии параболы.г) График функции расположен в I и II координатных четвертях. 1.D (f) = (- ∞ ; ∞)2.E (f) = [0; ∞)3.f (x) = 0,если х = 04.f (х) > 0,если х ≠ 05.f (x) возрастает в промежутке [0; ∞)6.f (x) убывает в промежутке [- ∞;0]7.f (x)наиб. не существует8.f (x)наим. = 0, при х = 09.f (-x) = f (x)Функция является четной.

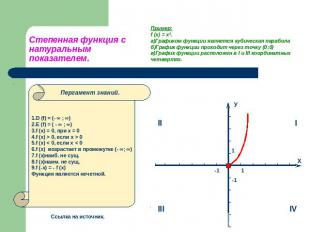
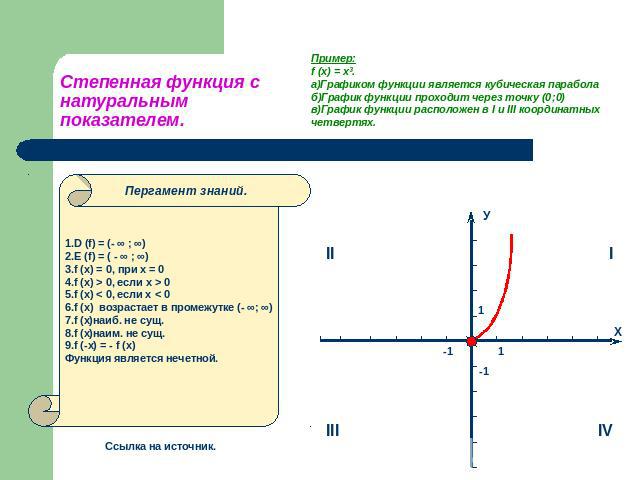
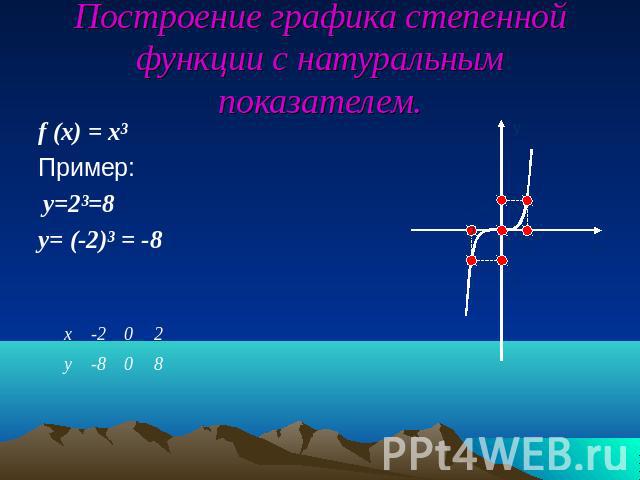
Степенная функция с натуральным показателем. Пример:f (x) = x³.а)Графиком функции является кубическая параболаб)График функции проходит через точку (0;0) в)График функции расположен в I и III координатных четвертях. 1.D (f) = (- ∞ ; ∞)2.E (f) = ( - ∞ ; ∞)3.f (x) = 0, при х = 0 4.f (x) > 0, если x > 05.f (x) < 0, если х < 06.f (x) возрастает в промежутке (- ∞; ∞)7.f (х)наиб. не сущ.8.f (х)наим. не сущ.9.f (-x) = - f (x)Функция является нечетной.

Линейная функция. Пример:f (x)= 2x + 1а) Графиком функции является прямая, б)График функции проходит через точки (-0,5;0) и (0;1) 1.D (f) = (- ∞;∞)2.E (f) = ( - ∞;∞)3.f (x) = 0 ,при x= -0.54.f (x) > 0, если x > -0,55.f (x) < 0, если x < -0,56.f (x) возрастает на всей области определения8.f (x)наиб. не сущ.9.f (x)наим. не сущ.10.Функция не является ни четной, ни нечетной.

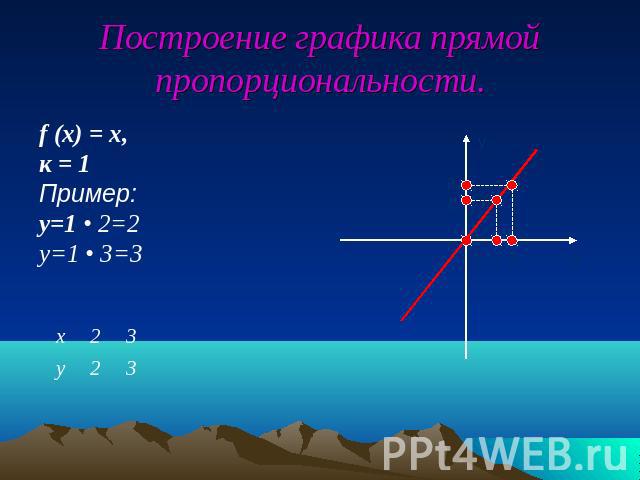
Прямая пропорциональность. Пример:f (x) = kx, k>0а)Графиком функции является прямая;б)График функции проходит через точку (0;0)в)График функции расположен в I и III координатных четвертях. 1.D (f) = (- ∞; ∞)2.Е (f) = ( - ∞; ∞)3.f (x) = 0, при х = 04.f (x) > 0, при x > 05.f (x) < 0, при x < 06.f (x) возрастает в промежутке (- ∞; ∞), т.е. на всей числовой прямой.7.f (x)наиб.- не сущ.8.f (x)наим.- не сущ.9.f (-x) = - f (x)Функция является нечетной.

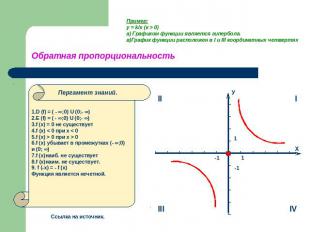
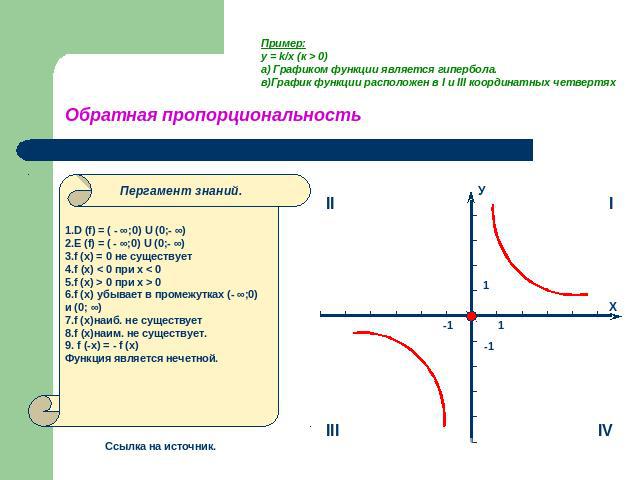
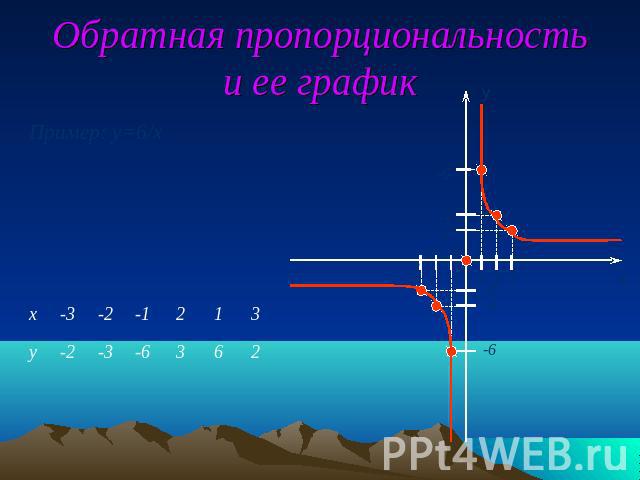
Пример:y = k/x (к > 0)а) Графиком функции является гипербола.в)График функции расположен в I и III координатных четвертях Обратная пропорциональность 1.D (f) = ( - ∞;0) U (0;- ∞)2.E (f) = ( - ∞;0) U (0;- ∞)3.f (x) = 0 не существует4.f (x) < 0 при х < 05.f (x) > 0 при x > 06.f (x) убывает в промежутках (- ∞;0)и (0; ∞)7.f (x)наиб. не существует8.f (x)наим. не существует.9. f (-x) = - f (x)Функция является нечетной.

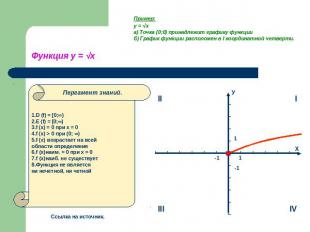
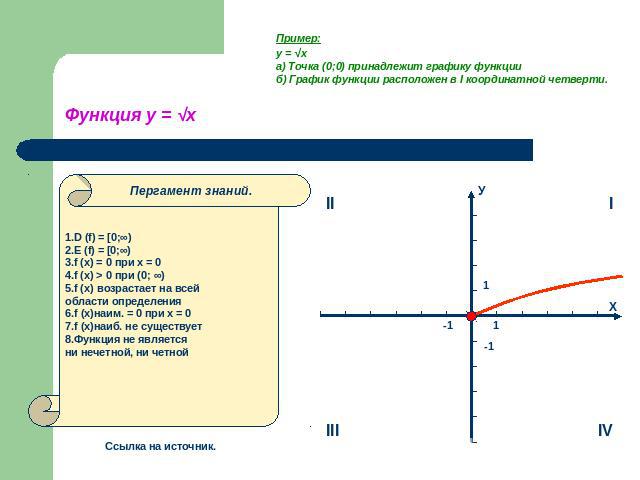
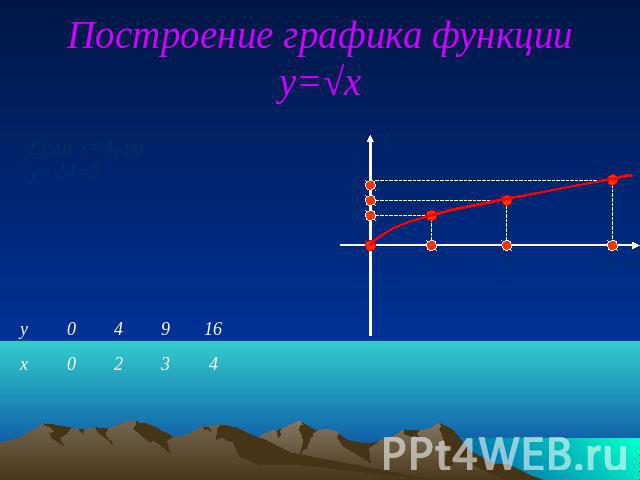
Пример:y = √xа) Точка (0;0) принадлежит графику функцииб) График функции расположен в I координатной четверти. Функция у = √х 1.D (f) = [0;∞)2.E (f) = [0;∞)3.f (x) = 0 при x = 04.f (x) > 0 при (0; ∞)5.f (x) возрастает на всейобласти определения6.f (x)наим. = 0 при х = 07.f (x)наиб. не существует8.Функция не являетсяни нечетной, ни четной

Пример построения графика квадратичной функции. F(x)= 2x² + 8x +21) Ветви 2) х = -8 ∕ 2•2= -2 y = f(x ) = 2•(-2)² + 8•(-2)+2= -6 С (-2;-6) 3) х=-2 ( ось симметрии параболы)4)

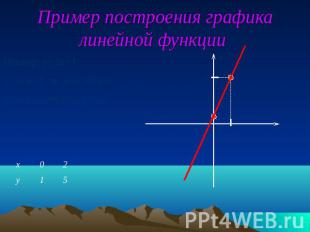
Пример построения графика линейной функции

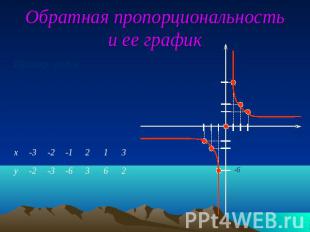
Обратная пропорциональность и ее график

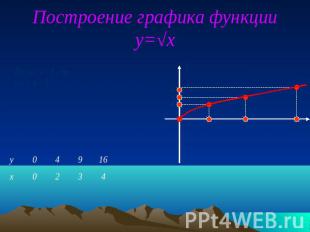
Построение графика функции y=√x

Построение графика прямой пропорциональности.f (x) = x, к = 1Пример: y=1 • 2=2y=1 • 3=3

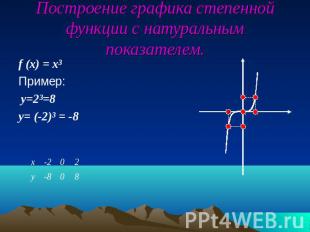
Построение графика степенной функции с натуральным показателем.f (x) = x³Пример: y=2³=8y= (-2)³ = -8

авторы:Ю.Н. МакарычевН.Г. МиндюкК.И. НешковС.Б. Суворова Издательство: Просвещение. Кликните на картинку, что бы перейти на Интернет ресурс, по учебнику.

Спасибо за внимание. Желаем успехов.