Презентация на тему: Тригонометрические функции и их графики

Тригонометрические функциии их графики

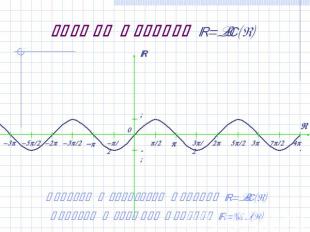
График функции y=sin(x) Переход к свойствам функции y=sin(x)Переход к графику функции y=cos(x)

Свойства функции y=sin(x) Область определения y=sin(x) – множество R всех действительных чисел.Множество значений y=sin(x) – отрезок [-1;1].Функция периодическая: sin(x)=sin(x+2pn) , nZ.Функция нечётная: sin(x)=-sin(-x).Функция принимает нулевые значения в точках, кратных p.Функция y=sin(x) принимает максимальное значение, равное 1, в точках x=p/2 + 2pn, nZ.Функция y=sin(x) принимает минимальное значение, равное -1 в точках x=-p/2 + 2pn , nZ.Между этими точками функция y=sin(x) монотонно убывает или монотонно возрастает.Вернись обратно к графику и найди на нём все указанные свойства функции y=sin(x) !

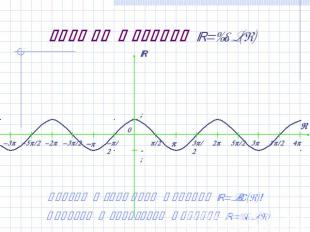
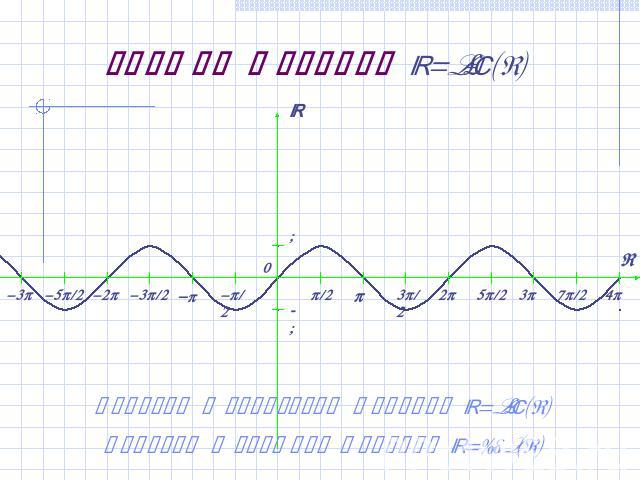
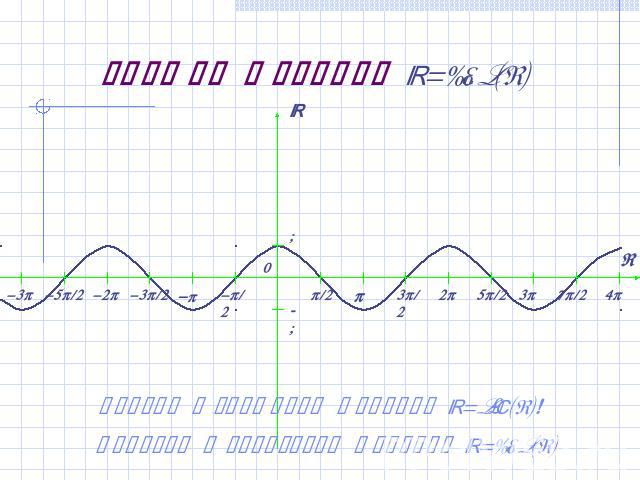
График функции y=cos(x) Сравни с графиком функции y=sin(x)! Переход к свойствам функции y=cos(x)

Свойства функции y=cos(x) Область определения y=cos(x) – множество R всех действительных чисел.Множество значений y=cos(x) – отрезок [-1;1].Функция периодическая: cos(x)=cos(x+2pn) , n Z.Функция чётная: cos(x)=cos(-x).Функция y=cos(x) принимает нулевые значения в точках x=p/2 + pn , n Z.Функция y=cos(x) принимает максимальное значение, равное 1, в точках x=2pn , n Z.Функция y=cos(x) принимает минимальное значение, равное -1 в точках x= (2n+1 ) p, n Z.Между этими точками функция y=cos(x) монотонно убывает или монотонно возрастает.Вернись обратно к графику и найди на нём все указанные свойства функции y=cos(x) !

Преобразования графиков функций sin(x) и cos(x) y= -sin(x)y= sin(x-)y= sin(x+/2)y= sin(x-/4)y= sin(x)+2y= 2sin(x)-1y= 2sin(x-/4)-1y= -cos(x)y= cos(x+)y= cos(x-/2)y= cos(x+/4)y= cos(x)-1y= 2cos(x)+1y= 2cos(x+/4)+1

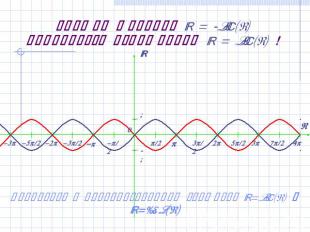
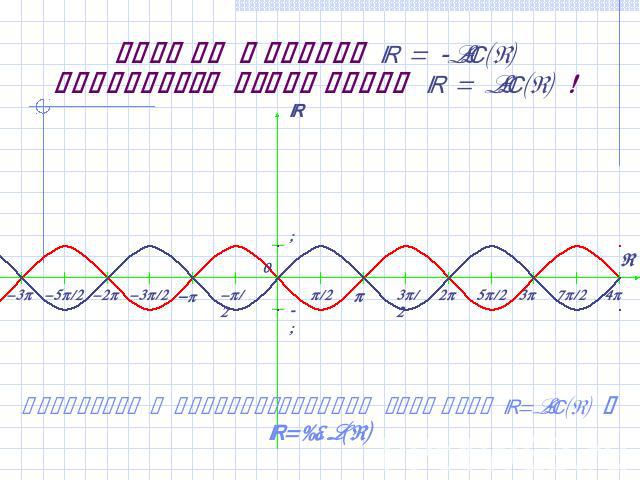
График функции y = -sin(x) получается отражением y = sin(x) ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

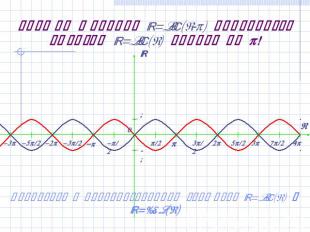
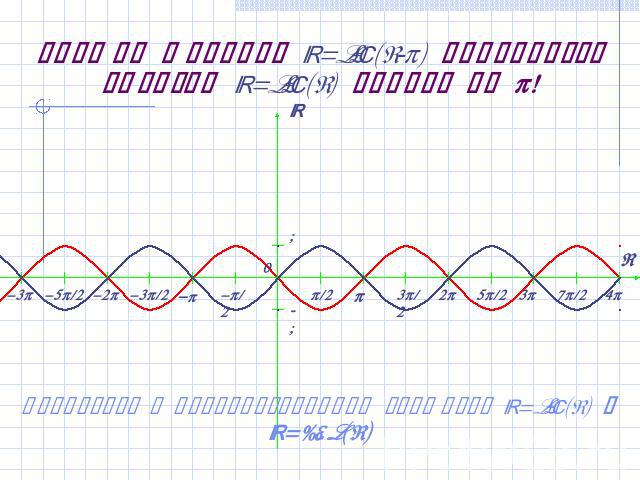
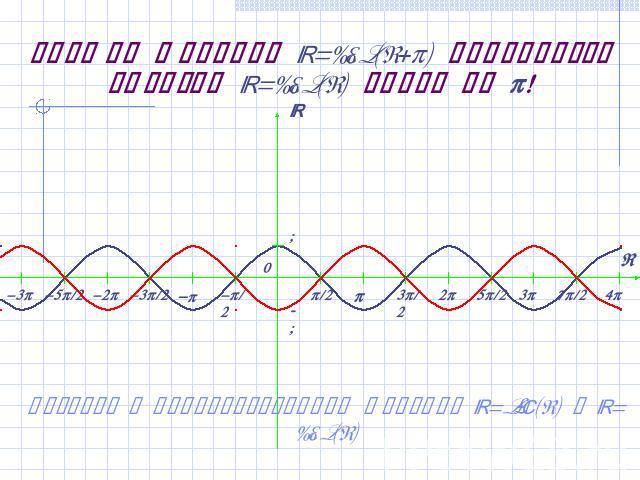
График функции y=sin(x-) получается сдвигом y=sin(x) вправо на ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

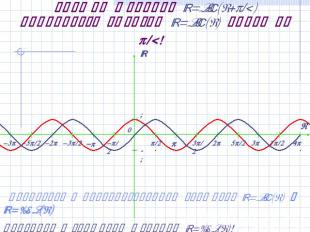
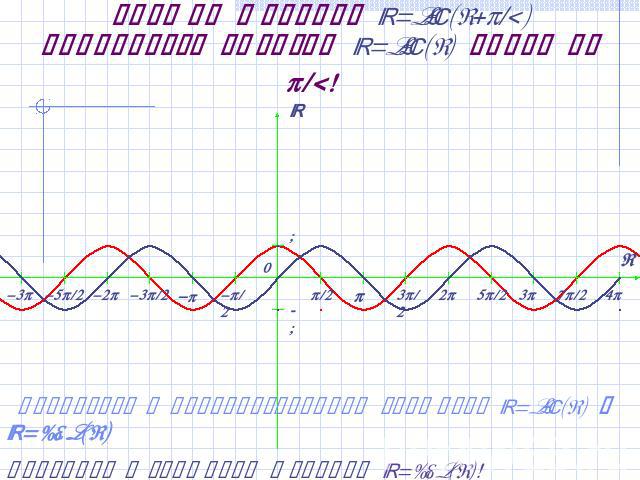
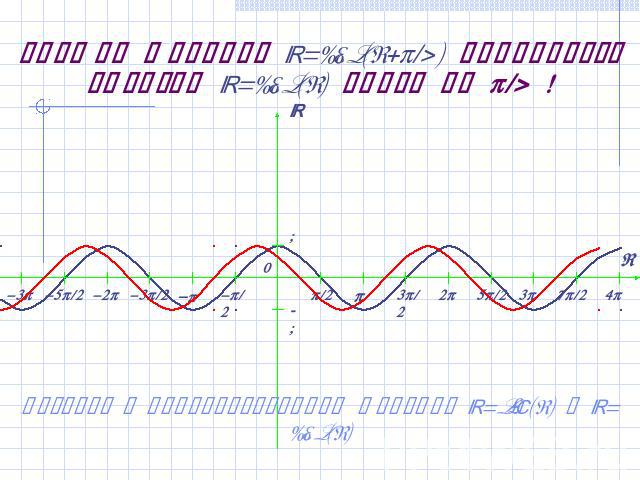
График функции y=sin(x+/2) получается сдвигом y=sin(x) влево на /2! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)Сравните с графиком функции y=cos(x)!

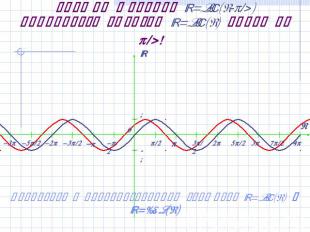
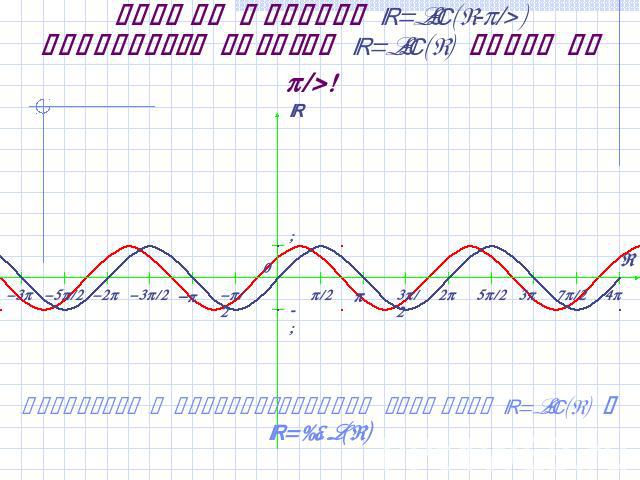
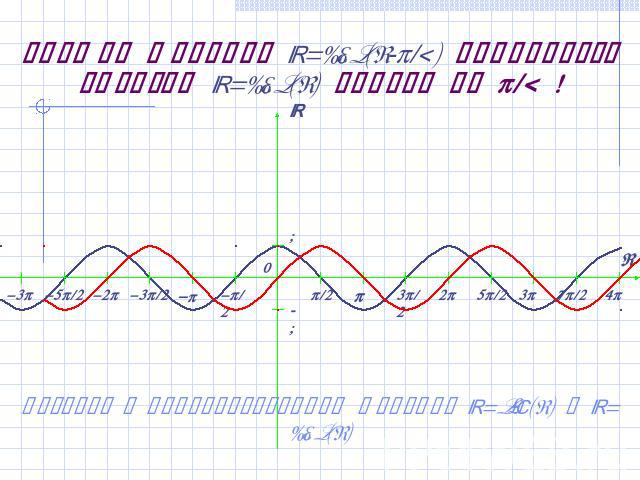
График функции y=sin(x-/4) получается сдвигом y=sin(x) влево на /4! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

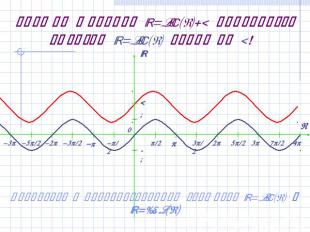
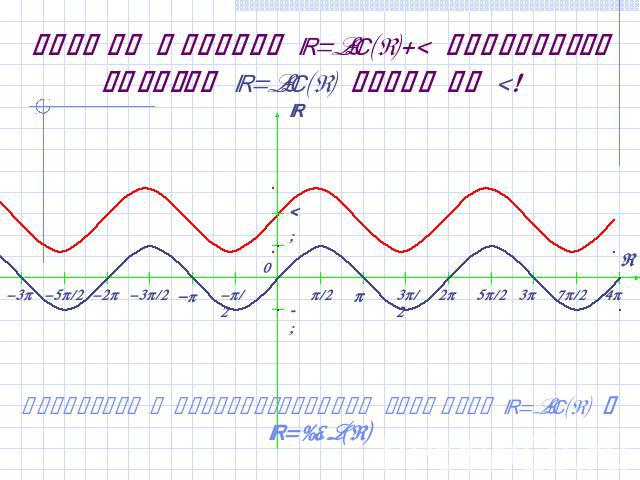
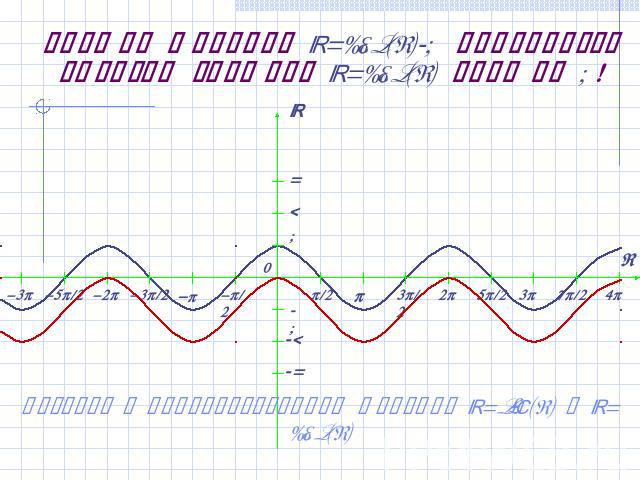
График функции y=sin(x)+2 получается сдвигом y=sin(x) вверх на 2! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

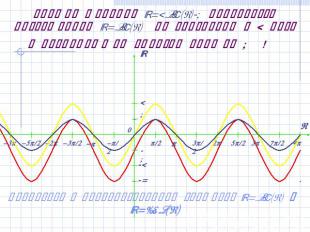
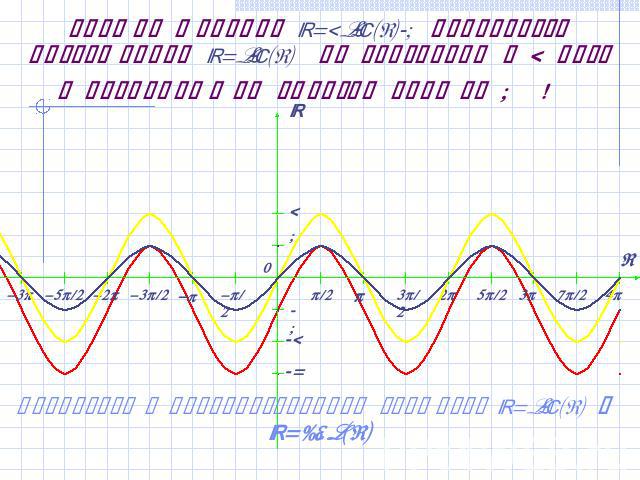
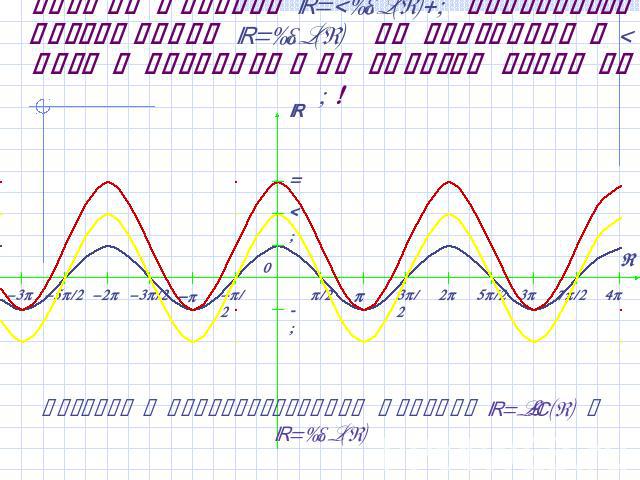
График функции y=2sin(x)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 ! Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

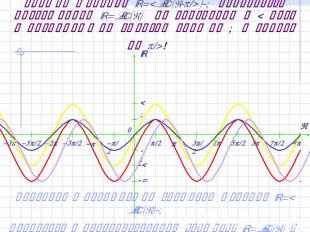
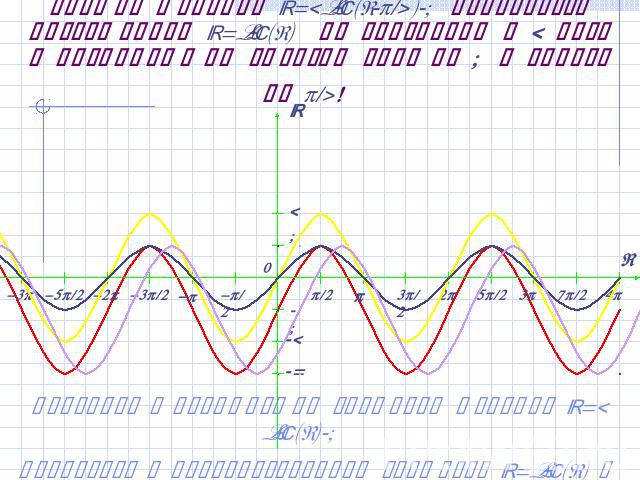
График функции y=2sin(x-/4)-1 получается растяжением y=sin(x) по вертикали в 2 раза и последующим сдвигом вниз на 1 и вправо на /4! Сравните с предыдущим графиком функции y=2sin(x)-1 Вернуться к преобразованиям графиков y=sin(x) и y=cos(x)

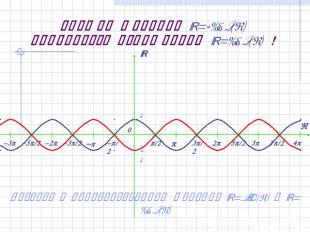
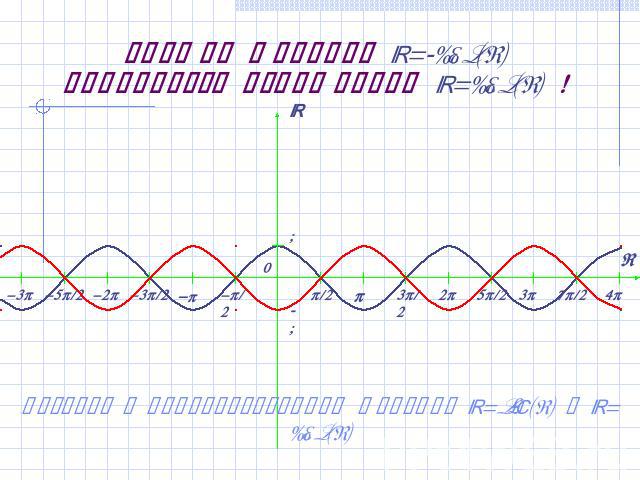
График функции y=-cos(x) получается отражением y=cos(x) ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

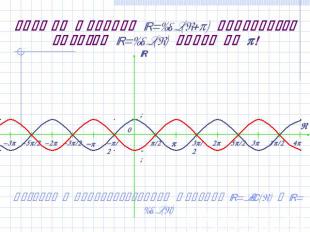
График функции y=cos(x+) получается сдвигом y=cos(x) влево на ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

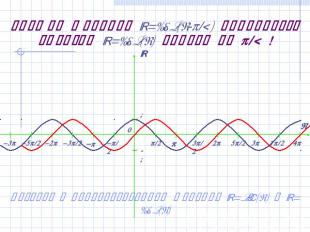
График функции y=cos(x-/2) получается сдвигом y=cos(x) вправо на /2 ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

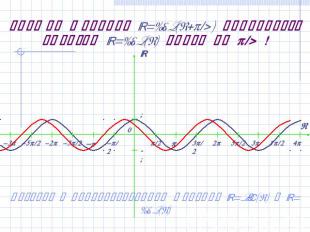
График функции y=cos(x+/4) получается сдвигом y=cos(x) влево на /4 ! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

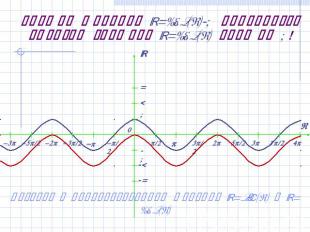
График функции y=cos(x)-1 получается сдвигом графика y=cos(x) вниз на 1! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

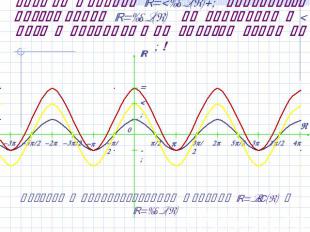
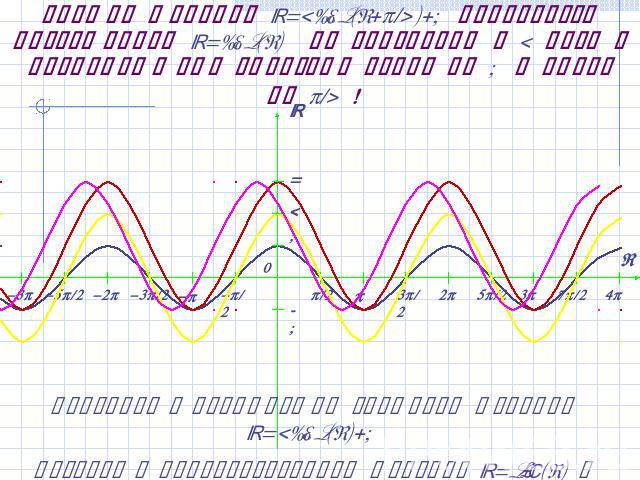
График функции y=2cos(x)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующим сдвигом вверх на 1! Возврат к преобразованиям функций y=sin(x) и y=cos(x)

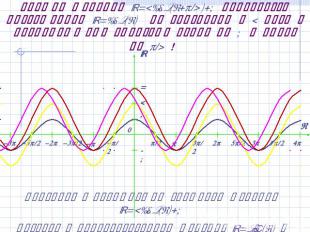
График функции y=2cos(x+/4)+1 получается растяжением y=cos(x) по вертикали в 2 раза и последующими сдвигами вверх на 1 и влево на /4 ! Сравните с предыдущим графиком функции y=2cos(x)+1Возврат к преобразованиям функций y=sin(x) и y=cos(x)