Презентация на тему: Логарифмы

Проект по теме : Логарифмы Работа выполнена учеником 11б класса МОУ Алексеевская СОШ Носовым Данилой Под руководством учителя математики Плешаковой Ольги Владимировны 2010 год

Содержание 1)Из истории2)Определение логарифма3)Свойства логарифмов4)Виды логарифмов5)Источники информации

Из истории Джон Непер (1550—1617) — шотландский барон, математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц.

В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание.

В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введённый для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом (ln) следующим образом:LogNap(x) = M * (ln(M) – ln(x)) Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса»есть нуль — этого и добивался Непер своим определением LogNap(0) = ∞Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую.

Определение логарифма Log a bЛогарифмом числа b по основанию a называется показатель степени,в которую нужно возвести основаниеa,чтобы получить число bПример log 2 8 = 3

Свойства a log a b = b – основное логарифмическое тождество Log a a = 1 Log a 1 = 0 Log a xy = log a x + log a y Log a x/y = log a x – log a y Log a xp= p log a x Log ak b = 1/k log a b Log aq bp = p/q log a b Log ak bk = log a b

Формула перехода Log a x = log b x/log b aДоказательствоПо правилу логарифмирования степени и основному логарифмическому тождеству получаем Log b x = log b ( a log a x )Log b x = log a x log b aРазделив обе части полученного равенства на log b a , приходим к нужной формуле

Вещественный логарифм Логарифм вещественного числа log a b имеет смысл при a>0,a не равное 1,b>0Наиболее распространённые:десятичные(основание - 10)натуральные(основание е – число Эйлера)двоичные(основание – 2)

Десятичный логарифм Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки.

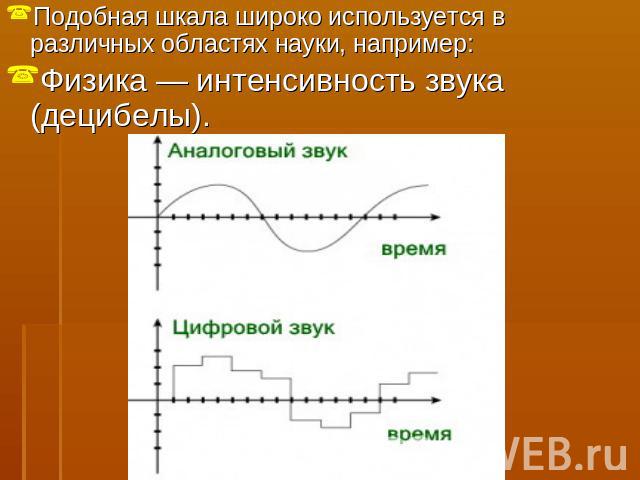
Подобная шкала широко используется в различных областях науки, например:Физика — интенсивность звука (децибелы).

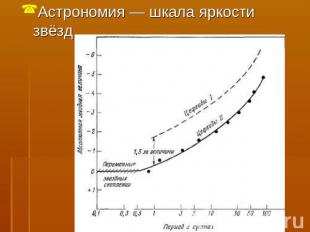
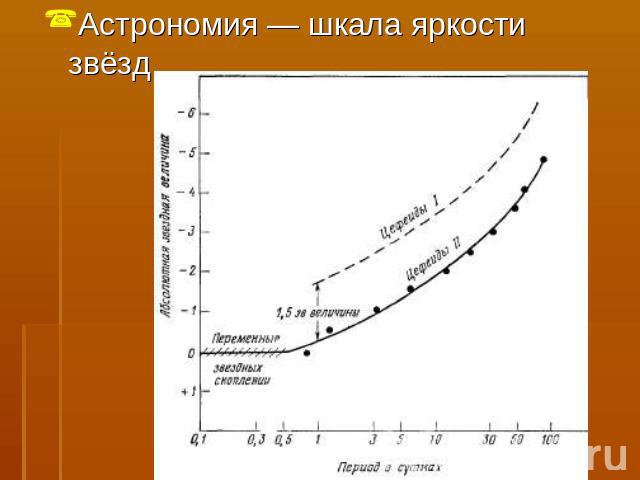
Астрономия — шкала яркости звёзд

Сейсмология — шкала Рихтера.

Теория музыки — нотная шкала, по отношению к частотам нотных звуков.История — логарифмическая шкала времени.

Химия — активность водородных ионов(pH) Логарифмическая шкала также широко применяется для выявления показателя степени в степенных зависимостях и коэффициента в показателе экспоненты. При этом график, построенный в логарифмическом масштабе по одной или двум осям, принимает вид прямой, более простой для исследования.

Для рациональных чисел, отличных от 10k с целыми k, десятичные логарифмы суть трансцендентные числа, которые приближенно выражаются в десятичных дробях. Целую часть десятичного логарифма называют характеристикой, дробную - мантиссой. Так как lg(10kN) = k + lnN, то десятичные логарифмы чисел, отличающихся множителем 10k, имеют одинаковые мантиссы и различаются лишь характеристиками. Это свойство лежит в основе построения таблиц логарифмов, которые содержат лишь мантиссы логарифмов целых чисел.

Натуральный логарифм Логарифм по основанию e (e трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.

Логарифмическая функция Логарифмической функцией называется функция вида f(x) = log a x, определённая при a>0 , x > 0

Источники http://ru.wikipedia.org/wiki/%D0%9B%D0 BE%D0%B3%D0%B0%D1%80%D0%B8%D1%84%D0%BChttp://logarithm.org.ua/Учебник «Алгебра и начало анализа» 10-11 класса (А.Н.Колмлгоров,А.М.Абрамов,Ю.П.Дудницын,Б.М.Ивлёв,С.И.Шварцбурд)