Презентация на тему: Логарифмы

Логарифмы

Содержание Логарифмы Свойства логарифмов Десятичные и натуральные логарифмы Формула перехода Логарифмические уравнения

Логарифмы Логарифмом положительного числа b по основанию a, где a>0, a=1, называется показатель степени ,в которую надо возвести a , чтобы получить b Например, log 28=3, так как 2³=8 log3 =-2, так как 3-2 = Определение логарифма можно кратко записать так: alog b =b Например, 4log 5 =5

Свойства логарифмов При выполнении преобразований выражений, содержащих логарифмы ,при вычислениях и при решений уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них Пусть a>0, a= 1, b>0< c>0, r- любое действительное число. Тогда справедливы формулы: loga (bc)=logab +logac loga =logab - logac

Десятичные и натуральные логарифмы Определения Десятичным логарифмов числа логарифм этого числа по основанию 10 и пишут lg b вместо log10 b. Натуральным логарифмов числа называют логарифм этого числа по основанию e, где e – иррациональное число, приближенно равное 2,7. При этом пишут ln b вместо loge b

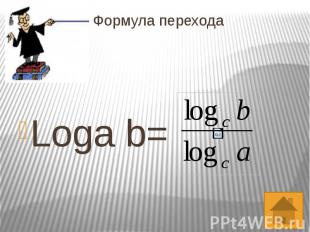
Формула перехода Loga b=

Логарифмические уравнения       Уравнение F(x) = 0 называется логарифмическим, если его левая часть F(x) образована из функций вида loga x, loga f(x) или logg(x) f(x) и констант с помощью конечного числа арифметических операций (сложения, умножения, деления). Примеры логарифмических уравнений: 1. log2 (x – 3) = 5; 3. log x–1 9 = 2; 2. lg x + lg (x + 3) = 1;  4. log3 (x2 – 3x – 5) = log3 (7 – 2x). В пособии рассматриваются несколько методов решения и, соответственно, несколько классов логарифмических уравнений, с обзором которых можно познакомиться в пункте «Развернутое содержание» (буква С)