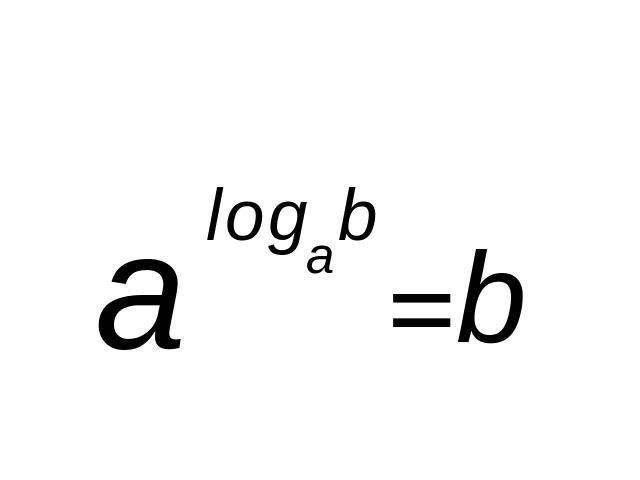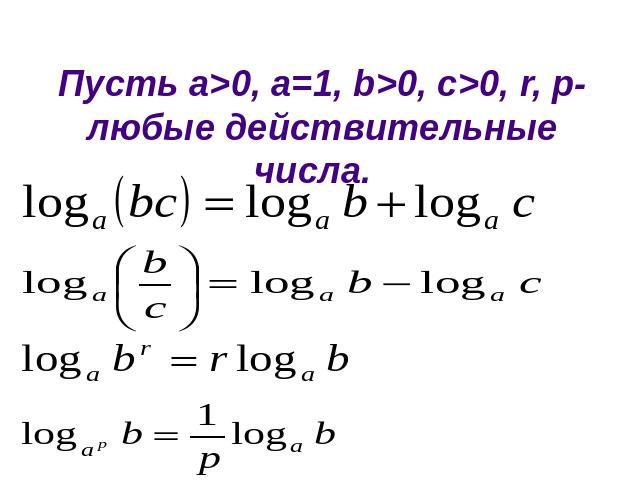Презентация на тему: Логарифмы с параметрами

Проект по алгебре на тему: «Логарифмы с параметрами»Авторы:Балаев Игорь, Калашников Иван, Редькин Александр.

ВведениеИзучение многих физических процессов и геометрических закономерностей часто приводит к решению уравнений, содержащих параметр. Решение задач с параметрами вызывает большие трудности у учащихся, так как их изучение не является отдельной составляющей школьного курса математики, и рассматривается только на немногочисленных факультативных занятиях. Между тем, параметрические уравнения, в том числе и логарифмические, входят в состав сборников ЕГЭ. А ЕГЭ сдавать придется каждому.Данный проект должен помочь в изучении таких интересных тем, как «Логарифмы» и «Параметры», а так же должен помочь при подготовке к единому государственному экзамену.

Анализ ситуацииЛогарифмы, а тем более с параметрами – вещь очень сложная. Поэтому перед началом проекта был проведен опрос в нашем классе (22 человека, 3 не участвовали в опросе) : «Можете ли вы решать логарифмы с параметрами?».Результаты (представлены в диаграмме) оказались очень интересными:

Результаты опроса

Как мы видим из результатов опроса, логарифмические уравнения с параметрами особой популярностью не пользуются. Но это и не удивительно: чтобы их решать, нужно знать все о логарифмах.

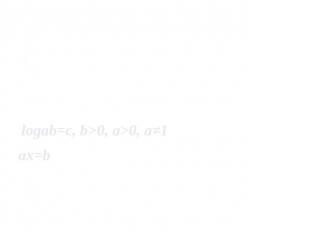
Определение логарифмаЛогарифмом положительного числа в по основанию а, где а>0,a≠1,называется показатель степени c, в которую нужно возвести число а ,чтобы получилось в. logab=c, b>0, a>0, a≠1ax=b

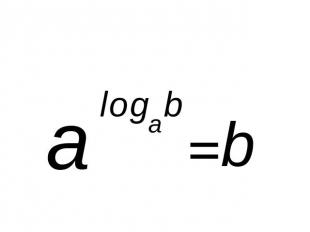
Основное логарифмическое тождество

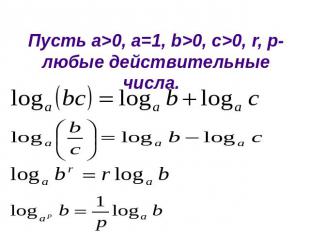
Свойства логарифмовПусть а>0, a=1, b>0, c>0, r, p-любые действительные числа.

ПараметрыС логарифмами и его свойствами разобрались, теперь приступим к параметрам.Определение: Параметрами называются переменные a, b, c, ..., k, которые при решении данного уравнения считаются постоянными.Решить уравнение, содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения

Виды логарифмических уравнений с параметрамиЛогарифмические уравнения с параметрами можно разделить на три вида в зависимости от местоположения параметра:Уравнения, содержащие параметры в логарифмируемом выражении.Уравнения, содержащие параметры в основании.Уравнения, содержащие параметры и в основании и в логарифмируемом выражении.

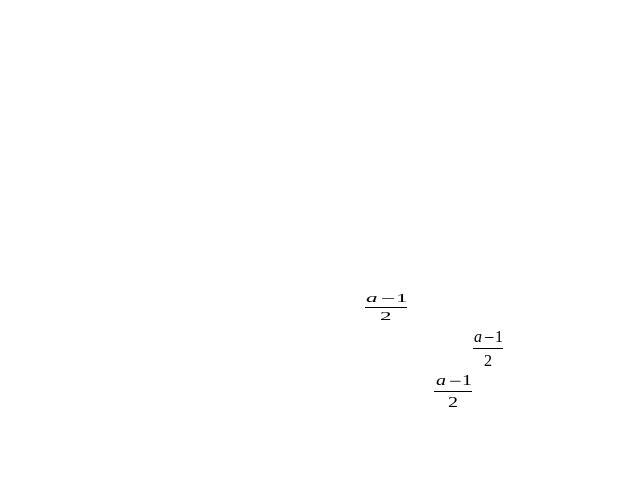
Уравнения, содержащие параметры в логарифмируемом выраженииРешить при всех a: logx + 1(x2 + a) = 2.Решение:Из определения логарифма следует, что x + 1 > 0, x + 1 ≠ 1 и x2 + a > 0. Получаем уравнение x2 + a = (x + 1)2. Из ограничения x + 1 > 0 следует, что x2 + a > 0. Следовательно, нужно найти решения уравнения x2+a= =(x+1)2, удовлетворяющие неравенствам x + 1 > 0 и x ≠ 0.Раскроем скобки в правой части уравнения: x2 + a = x2 + 2x + 1.Вычитая x2 + 2x + a из обеих частей уравнения, находим –2x = 1 – a,откуда получаем: x= Из ограничения x + 1 > 0 следует ˃0, откуда a – 1 + 2 > 0. Значит, a > –1. Из ограничения x ≠ 0 находим ≠0 , что влечет a ≠ 1.Ответ: Если a > –1, a ≠ 1, то одно решение x= . Если a ≤ –1 или a = 1, то решений нет.

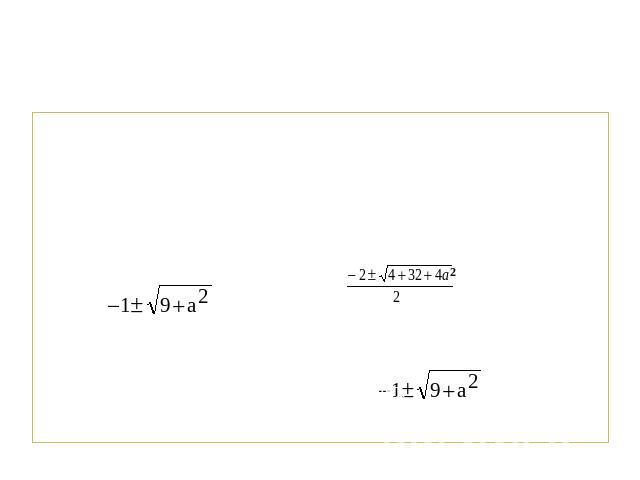
Уравнения, содержащие параметры в основанииРешить при всех а: loga(x2+2x-8)=2 Решение:Из определения логарифма следует, чтоa≠1, a>0, x2+2x-8>0(x<-4; x>2). Значит, требуется решить уравнение a2=x2+2x-8. Решая это уравнение, получаем х= или х= . Подкоренное выражение положительно при всех значениях а, поэтому дальнейших ограничений не последует.Ответ: Если a > 0, a ≠ 1, то x= . Если a ≤ 0 или a = 1, то решений нет.

Уравнения, содержащие параметры и в основании и в логарифмируемом выраженииРешить при всех a уравнение loga(ax + 1) = 1.Решение Из определения логарифма следует, что a >0, a≠1, ax + 1 > 0. Получаем уравнение ax + 1= a. Заметим, что так как a > 0, то ax + 1 = a > 0. Следовательно, надо решить уравнение ax +1= a при ограничениях на параметр a: a > 0, a ≠ 1. Вычитая из обеих частей уравнения единицу, получим ax = a – 1. Так как a > 0, то уравнение имеет единственное решение x= . Ответ: При a ≤ 0 и a = 1 решений нет. При a > 0 и a ≠ 1 одно решение x= .

Что дал этот проект?В процессе работы мы овладели начальными навыками решений параметрических уравнений, научились решать логарифмические уравнения с параметрами. Эта работа позволила нам лучше изучить и запомнить все свойства логарифмов. А главное, мы окончательно убедились в том, что есть вещи похуже проектной по технологии.

Результаты повторного опросаПо окончанию данного проекта был проведен повторный опрос на тему «Можете ли вы решать логарифмические уравнения с параметрами?». Результаты оказались намного лучше предыдущих: теперь все 100% (19 человек) ответили «не могу».

Над проектом работали:Редькин Александр (ka3ak)Балаев Игорь (STiciER)Калашников Иван (kalach)