Презентация на тему: Метод интервалов решения неравенств

Презентация подготовленаУчителем математики ГОУ СОШ №769Рыковой Т.М.Метод интервалов решения неравенств.

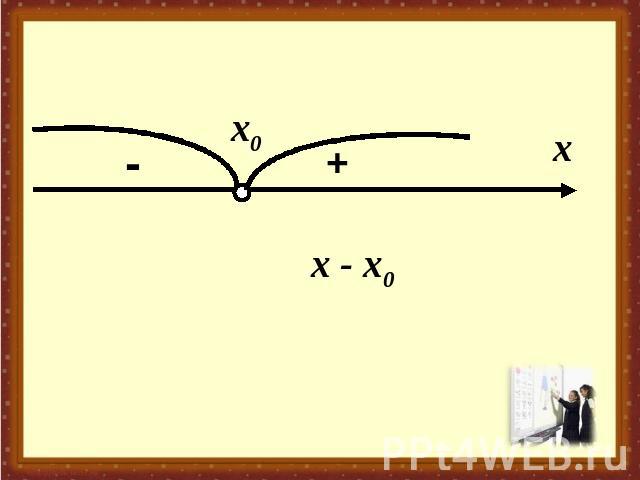
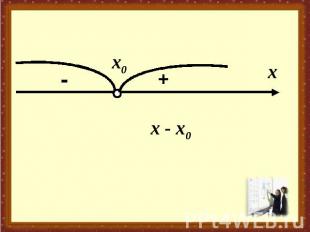
Решение неравенства Решением неравенства с неизвестным х называют число, при подстановке которого в это неравенство вместо х получается верное числовое неравенство.Решить неравенство – значит найти все его решения или показать, что их нет.

Рассмотрим способ решения неравенств вида: (х - х1) (х - х2)· … · (х - хn) > 0и(х - х1) (х - х2)· … · (х - хn) < 0, гдех1 < х2 < … < хn , n – натуральное число ( n ≥1).

Пусть требуется решить неравенство: (х - х1) (х - х2)(х – х3) > 0Или неравенство(х - х1) (х - х2)(х – х3) < 0, где х1 < х2 < х3

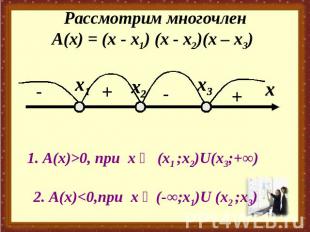
Рассмотрим многочленА(х) = (х - х1) (х - х2)(х – х3) 1. А(х)>0, при x ϵ (x1 ;x2)U(x3;+∞) 2. А(х)<0,при x ϵ (-∞;x1)U (x2 ;x3)

Метод интервалов На оси абсцисс отмечают точки х1;х2;х3;Над интервалом (х3;+∞) ставят знак «+»Над интервалом (х2;х3) ставят знак «-»Над интервалом (х1;х2) ставят знак «+»Над интервалом (-∞;х1) ставят знак «-»Решение неравенства

Пример 1 Решим неравенство: (х-2)(х-3)(х-4)>0.Отметим на оси ОХ точки 2;3;4Над интервалами(4;+∞);(3;4);(2;3);(-∞;2) справа налево поставим поочередно знаки «+»; «-».Ответ:(2;3)U(4; +∞)

Пример 2 Решим неравенство: (2-х)(х2-4х+3)(х+1)>0Разложим квадратный трехчлен на множители:(2-х)(х-3)(х-1)(х+1)>0умножим обе части неравенства на -1(х-(-1))(х-1)(х-2)(х-3)<0Отметим на оси ОХ точки-1;1;2;3Ответ:(-1;1)U(2;3)

Пример3 Решим неравенство:(х-1)(х-3)(х2+х+1)<0Трехчлен х2+х+1 принимает только положительные значения(D<0). Наше неравенство равносильно (х-1)(х-3)<0Решая методом интервалов получимОтвет:(1;3)

Пример 4 Решим неравенство:(х-1)3(х-2)2(х-3)4(х-4)<0Для решения таких неравенств используют общий метод интервалов, он состоит в следующем:Отметим на оси ОХ точки 1;2;3;4, а затем в каждом интервале исследуем знак многочлена А(х)= (х-1)3(х-2)2(х-3)4(х-4) Ответ:(1;2)U (2;3) U(3;4).

Упражнения: Устно:2.60-2.632.66(а,в)2.67(а,в,д)2.68(а,в,д)2.69(а)2.72(а)

Домашнее задание: 2.66(б,г)2.67(б)2.68(б,г)2.72(б)