Презентация на тему: Производная показательной функции

Производная показательной функции.

План урока

Устная работа. Определение производной.Правила дифференцирования.Производные элементарных функций.Применение производной при исследовании функции.Уравнение касательной.

Устная работа.

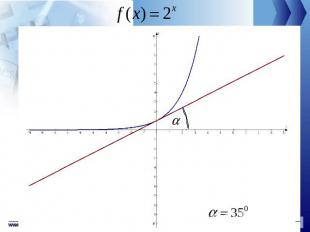
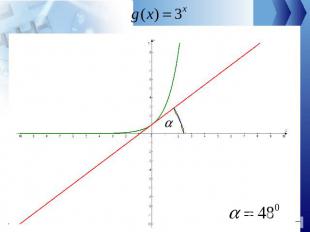
Функция Существует такое число большее 2 и меньшее 3 (это число обозначают буквой е), что показательная функция в точке 0 имеет производную, равную 1, т.е.

Теорема 1. Функция дифференцируема в каждой точке области определения, и

Определение Натуральным логарифмом называется логарифм по основанию е:

Теорема 2 Показательная функциядифференцируема в каждой точке области определения, и

Примеры. Найдите производную функцииРешение:

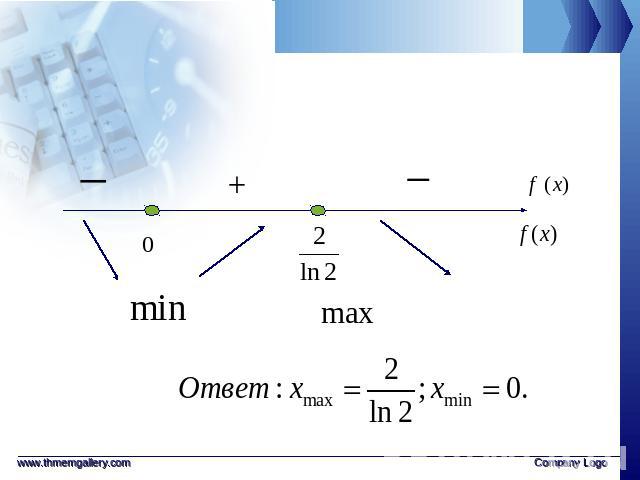
Примеры 2. Исследуйте функцию на экстремумы:Решение:

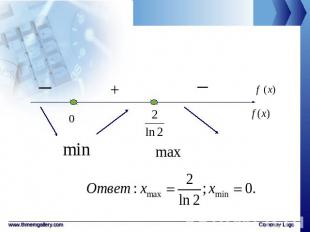
Теорема 3 Первообразной для функциина является функция

Примеры. 3. Вычислить интеграл

Решение примеров. № 1617№ 1618(абв)№ 1619(вг)№ 1620(вг)№ 1624 (аб)№ 1627 (б)№ 1631 (бг)

Задание на дом Пункт 41№ 538№ 539№ 540 (ав)№ 542(абв)