Презентация на тему: Производная и ее применение

МОУ СОШ 256г.Фокино.роизводнаяи ее применение.11 класс.. Геометрический смысл производной2. Механический смысл производной.

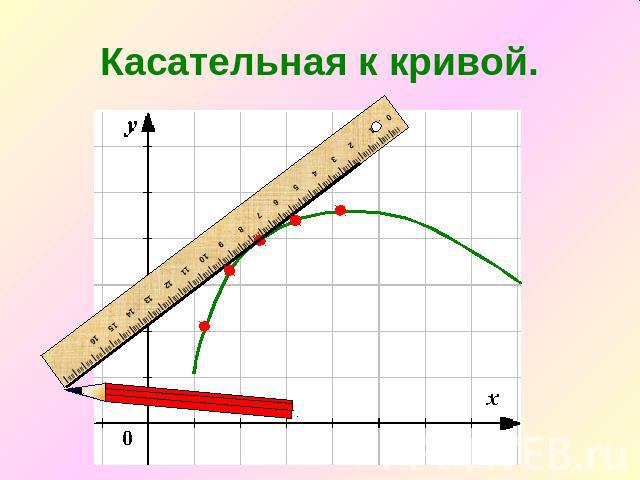
1. Геометрический смысл производной.Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой.»

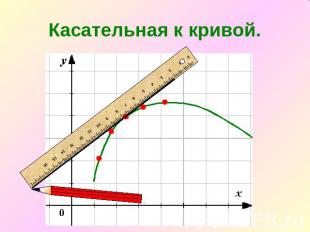
Касательная к кривой.

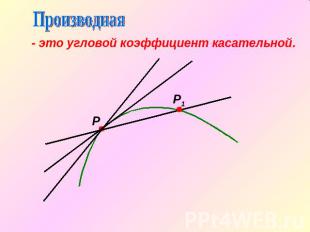
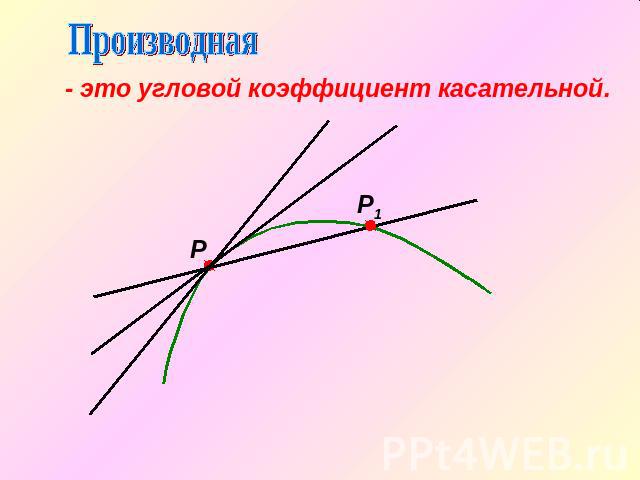
Производная- это угловой коэффициент касательной.

Повторение.Угловой коэффициент прямой.Прямая проходит через начало координат и точку Р(3; -1). Чемуравен ее угловой коэффициент?

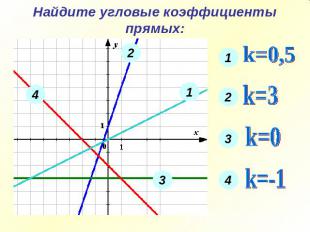
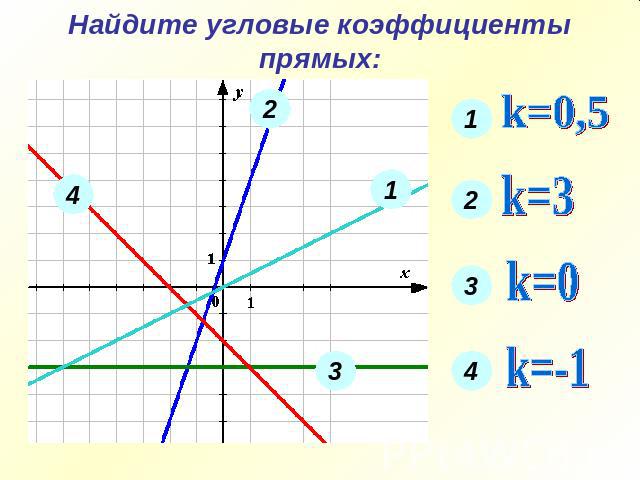
Найдите угловые коэффициенты прямых:

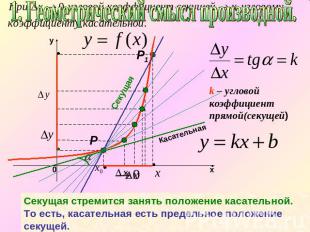
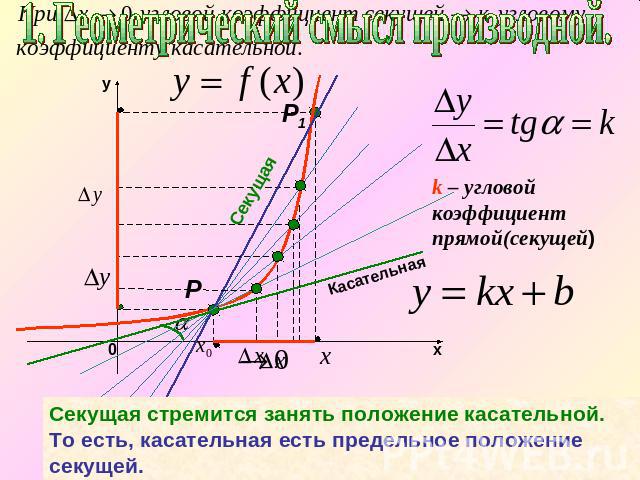
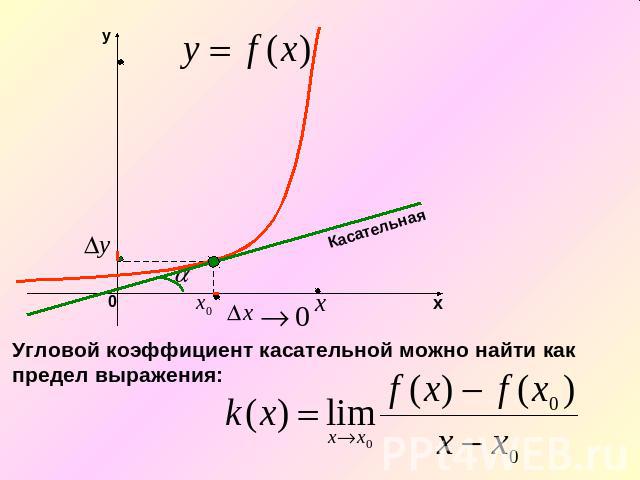
1. Геометрический смысл производной.угловой коэффициент прямой(секущей)Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.

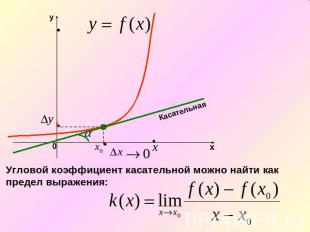
Угловой коэффициент касательной можно найти какпредел выражения:

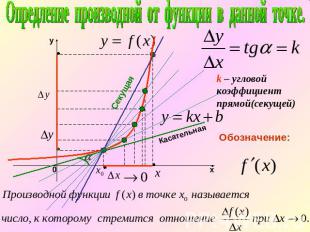
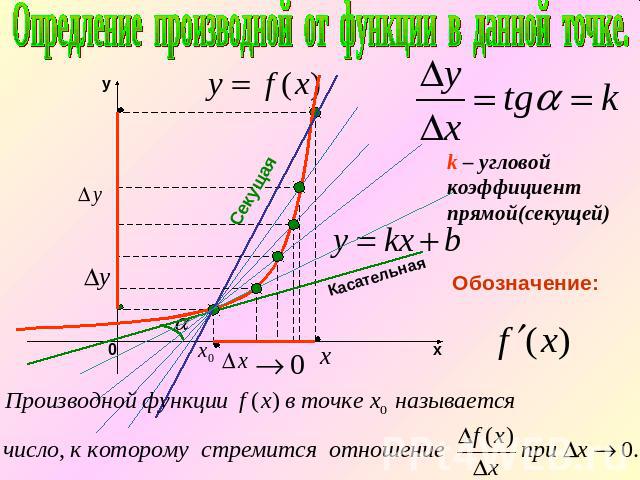
Опредление производной от функции в данной точке.– угловой коэффициент прямой(секущей)Обозначение:

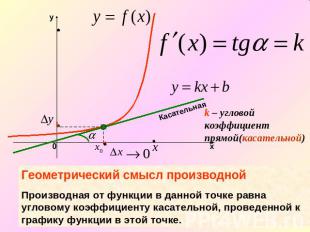
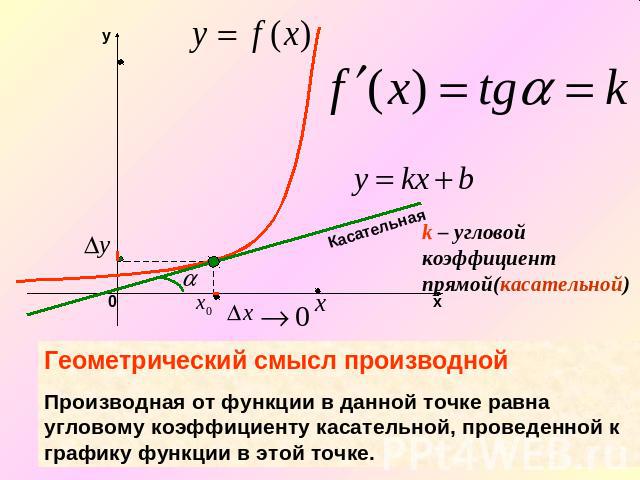
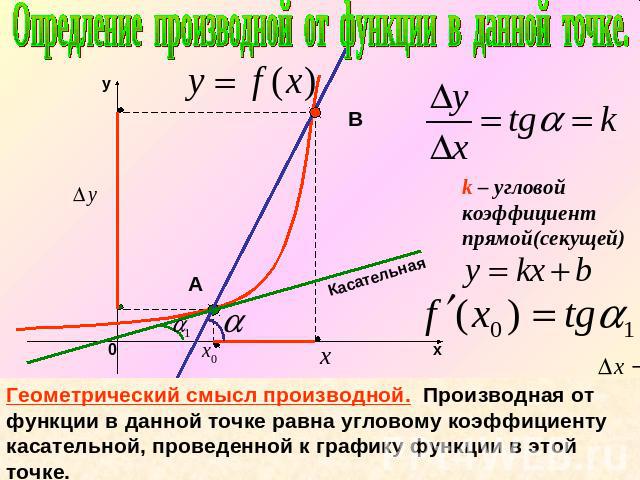
Геометрический смысл производнойПроизводная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

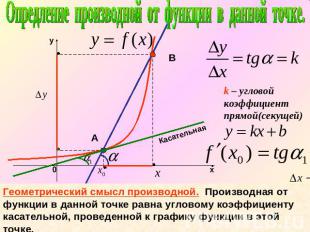
Опредление производной от функции в данной точке.k – угловой коэффициент прямой(секущей)Геометрический смысл производной. Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

2. Механический смысл производной.Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад.»

2. Механический смысл производной.Свободное падение

2. Механический смысл производной.Свободное падение

2. Механический смысл производной.Используя слово «предел», можно сказать, что мгновенная скорость в точке t – это предел средней скорости при стягивании отрезка, на котором она изменяется, в точку t или в символической записи

2. Механический смысл производной.– перемещение телапромежуток временив течение которого выполнялосьдвижение