Презентация на тему: Производная и её применение

МОУ «Матреногезовская средняя общеобразовательная школа» Урок – семинар«Производная и её применение» Подготовила: учитель математики и информатики Бутенко О.В. Директор школы : Заика А.И.

Цели урока: Общеобразовательные:*Углубление понимания сущности производной путём применения её для получения новых знаний;*Установление межпредметных связей;Воспитательные:*Воспитание познавательного интереса к учебному предмету;*Воспитание у учащихся культуры мышления;Развивающие:*формирование умений строить доказательство , логическую цепочку рассуждений;* формирование умений проводить рассуждение ,переносить знания в новую ситуацию.

План урока: 1.Вступительное слово учителя.2. Разгадывание кроссворда.3.Исторические сведения( выступление учеников).4.Групповая работа.5. Индивидуальная работа.6.Итоги урока.7. Рефлексия.

1.Вступительное слово учителя Исторически понятие производной возникло из практики. Скорость неравномерного движения , плотность неоднородной материальной линии , а также тангенс угла наклона касательной к кривой и другие величины явились прообразом понятия производной. Возникнув из практики , понятие производной получило обобщаемый , абстрактный смысл, что ещё более усилило его прикладное значение. Создание дифференциального исчисления чрезвычайно расширило возможности применения математических методов в естествознании и техники.

2.Разгадывание кроссворда. 1.Французский математик 17 века Пьер Ферма определял эту линию так: «Прямая, наиболее тесно примыкающая к кривой в малой окрестности заданной точки». 2. В математике это понятие возникло в результате попыток придать точный смысл таким понятиям , как «скорость движения в данный момент времени» и «касательной к кривой в заданной точке». 3. Приращение какой переменной обычно обозначают ∆х? 4. Если существует предел в точке a и этот предел равен значению функции в точке а , то в этой точке функцию называют …5. Эта точка лежит внутри области определения функции , и в ней функция принимает самое большое значение по сравнению со значением в близких точках. 6. Эта величина определяется как производная скорости по времени. 7. Если функцию y=f(x)=g(h(x)) , где y=g(t) и t=h(x) - некие функции , то функцию f называют…

Ответы к кроссворду

3.Исторические сведения(план семинара сообщается учащимся за несколько дней. Возможна работа в группах. Наиболее подготовленные дети ищут информацию в дополнительной литературе, остальные пользуются учебником) 3а)Сообщения учащихся:*Общие сведения. *Непрерывность функции.*Точки разрыва. 3б)prezentazia 1.ppt

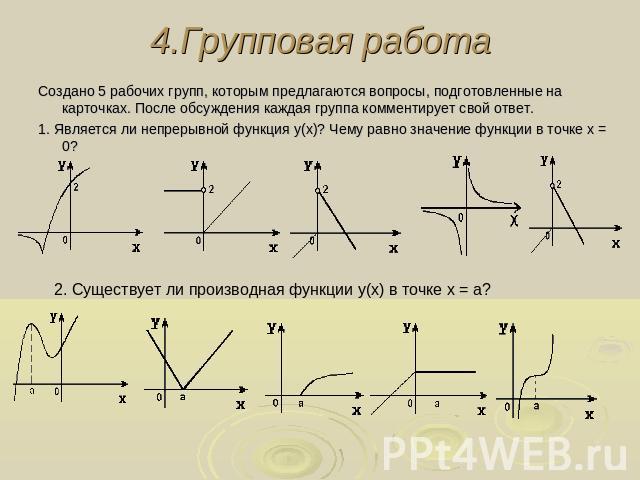
4.Групповая работа Создано 5 рабочих групп, которым предлагаются вопросы, подготовленные на карточках. После обсуждения каждая группа комментирует свой ответ.1. Является ли непрерывной функция y(x)? Чему равно значение функции в точке х = 0? 2. Существует ли производная функции y(x) в точке х = а?

5. Индивидуальная работа Выполнение тестовых заданий А) в тетрадях по индивидуальным карточкамБ) с использованием ПК

6. Итоги урока. А) объявление оценок;Б) объяснение домашнего задания.

7.Рефлексия. В конце урока каждый учащийся получает лист с изображением прямоугольной системы координат. Ось ОХ соответствует утверждению «полезно» , ось ОY- «интересно». Отметив точку в одной из четвертей, ученик показывает, на сколько интересен и полезен был для него урок.