Презентация на тему: Производная и её применение

Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью. Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью.

1.Исследование функции на монотонность 2.Касательная к графику. 3.Наибольшие, наименьшие значения функций. 4.Нахождение дифференциала для приближенных вычислений. 5.Доказательство неравенств.

Производной данной функции в точке х называется предел отношения приращения этой функции к приращению аргумента в точке х, когда приращение аргумента стремится к нулю. Производной данной функции в точке х называется предел отношения приращения этой функции к приращению аргумента в точке х, когда приращение аргумента стремится к нулю.

Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤ x ≤ b. Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤ x ≤ b. функция f(x) возрастает (или убывает) в промежутке a<x<b, если: производная f '(х) не отрицательна (или не положительна) в промежутке а<х<b, f '(x) ≥ 0 (или f '(x) ≤ 0) Пример. Определить промежутки возрастания и убывания функции: у = х3 — х2 — 8х + 2.

Решение: Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х, при которых она положительна или отрицательна: Решение: Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х, при которых она положительна или отрицательна: у' = Зх2 — 2х — 8. Корни трехчлена: x1= - 4/3, x2=2. Отсюда: у' =3(х+4/3)(х-2). возрастает убывает возрастает + -4/3 - 2 + Ответ: функция возрастает в промежутках - ∞ < x < -4/3 и 2 < x < + ∞ и убывает в промежутке — 4/3 < х <2.

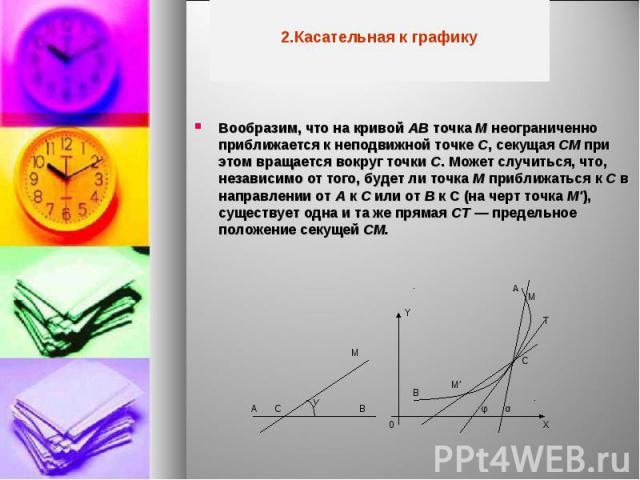
Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ. Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ.

Задача . В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и Задача . В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и DD1 =4 проведена плоскость через центр симметрии грани A1B1C1D1 , вершину А и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае?  

Пусть PC = x; ΔCLP подобен ΔDАР Пусть PC = x; ΔCLP подобен ΔDАР LC/AD = x/(24—x), LC = 6x/(24 – x). Из ΔCLP: KC = (6x ∙x/(24—x))/(√(36x2/(24—x)2)+x2) = = 6x/(√(36+ (24—x)2); Из ΔSCK: SK = √SC2+ KC2 = √64+36x2/(36+(24—x)2) = 2√16+9x2/(36+(24—x)2) ; Из ΔADP: AP = √36+(24—x)2; Sсеч = AP∙SK/2 = 0,5∙(√36+(24—x)2) 2√16+9x2/(36+(24—x)2) = =√16(36+(24—x)2)+9x2; Если S’(x) = 0, то 18x+16 ∙2(24—x)(-1) = 0; 50x—768 = 0, x = 384/25 (это точка min); Sсеч = 312; DP = 24—384/25 = 216/25; Ответ: 312 кв. ед.; DC- 384/25; 216/25.  

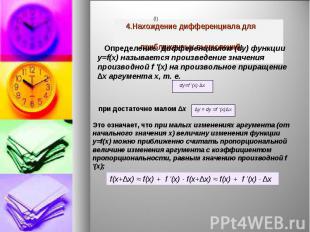
4.Нахождение дифференциала для 4.Нахождение дифференциала для приближенных вычислений.

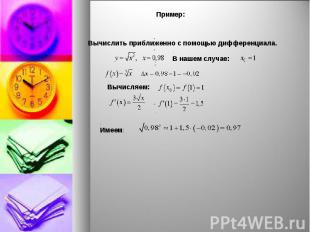
Пример:

Если функция f имеет положительную (отрицательную) производную в каждой точке некоторого промежутка, то она возрастает (убывает) на этом промежутке. При нахождении промежутков монотонности нужно иметь в виду, что если функция возрастает (убывает) на интервале (a,b) и непрерывна в точках a и b, то она возрастает (убывает) на отрезке [a,b]. Если функция f имеет положительную (отрицательную) производную в каждой точке некоторого промежутка, то она возрастает (убывает) на этом промежутке. При нахождении промежутков монотонности нужно иметь в виду, что если функция возрастает (убывает) на интервале (a,b) и непрерывна в точках a и b, то она возрастает (убывает) на отрезке [a,b].

Решение. Решение. Данное неравенство равносильно следующему: (e - x) ∙ln(e + x) > (e + x) ∙ln(e - x). Пусть f(x)=(e-x) ∙ln(e + x) - (e + x)∙ ln(e - x), тогда f/(x)= -ln(e + x)+(e - x)/(e + x) - ln(e - x)+(e + x)/(e - x). Так как (e - x)/(e + x)+ (e + x)/(e - x)=2(e2+x2)/(e2-x2) > 2, ln(e + x)+ln(e - x)=ln(e2-x2) < lne2 = 2, то f/(x) > 0 при 0 < x < e. Следовательно, функция f возрастает на интервале (0,e). Функция f(0) - непрерывна. Поэтому эту точку можно включить в промежуток возрастания. Поскольку f(0)=0, а f возрастает при 0 < x < e, то f(x) > 0 при 0 < x < e. Отсюда получаем решение задачи.