Презентация на тему: Производная 10 класс

Помни слова великого ученого: «Математику уже затем учить надо, что она ум в порядок приводит.» М.В.Ломоносов.

1. Выражение вида f появилось уже в конце 17 в. 1. Выражение вида f появилось уже в конце 17 в. и означает «приращение». 2. Термин производная ввел в 1797г. Ж. Лагранж 3.И. Ньютон называл производную функцию флюксией , а саму функцию – флюентой. 4.Раздел математики, в котором изучаются производные и их применения к исследованию функций , называется дифференциальным исчислением. 5.Дифференциальное исчисление создано Ньютоном и Лейбницем в конце 17 столетия.

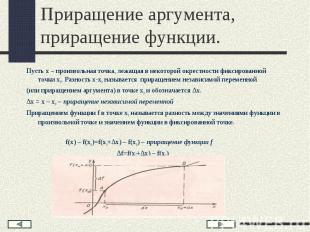
Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность х-х0 называется приращением независимой переменной Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность х-х0 называется приращением независимой переменной (или приращением аргумента) в точке х0 и обозначается ∆х. ∆х = х – х0 – приращение независимой переменной Приращением функции f в точке x0 называется разность между значениями функции в произвольной точке и значением функции в фиксированной точке. f(х) – f(х0)=f(х0+∆х) – f(х0) – приращение функции f ∆f=f(х0+∆х) – f(х0)

Геометрический смысл производной со- Геометрический смысл производной со- стоит в том, что производная в точке х0 равна угловому коэффициенту касательной в точке х0 и тангенсу угла наклона касатель- ной k=tgα=∆y/∆x

Механический смысл производной состо- Механический смысл производной состо- ит в том, что производная пути по време- ни равна мгновенной скорости в момент времени t0: S'(t0)=V(t0).

Найди производную функций: Найди производную функций: у=(7х+3)3 у=х2/х+3 у=3х4+sinx+5 y= tgx+3sin2x Найди тангенс угла наклона касательной, проведённой к графику функции у=-4/х в точке с абсциссой равной -3. Найди значение производной функции у=хcosх в точке х0=π. Решить уравнение f'(x)=0,если f(x)=x3-2x2

Желаем успехов Желаем успехов в изучении математики!