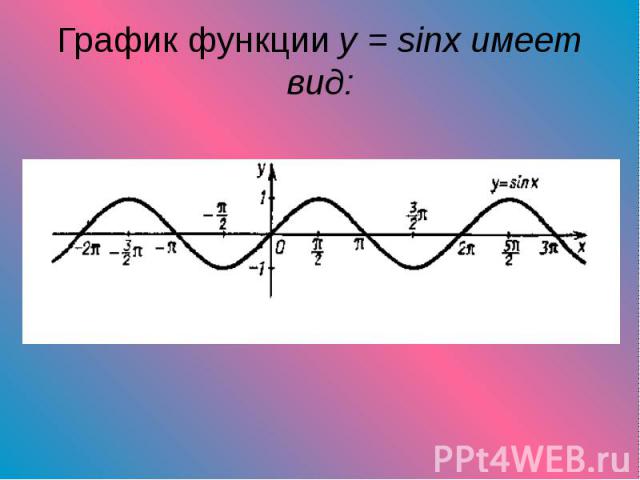
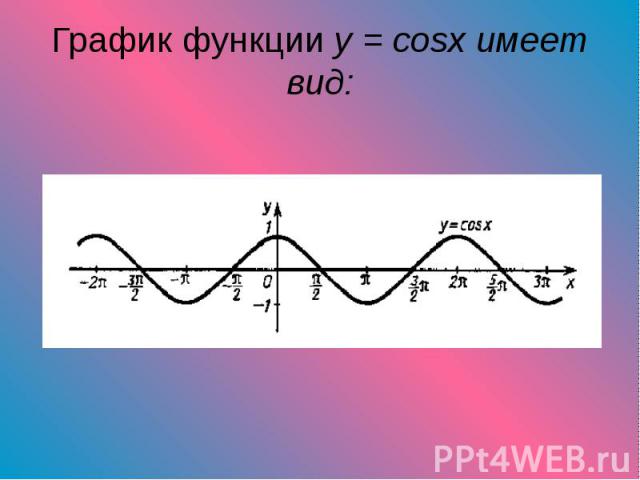
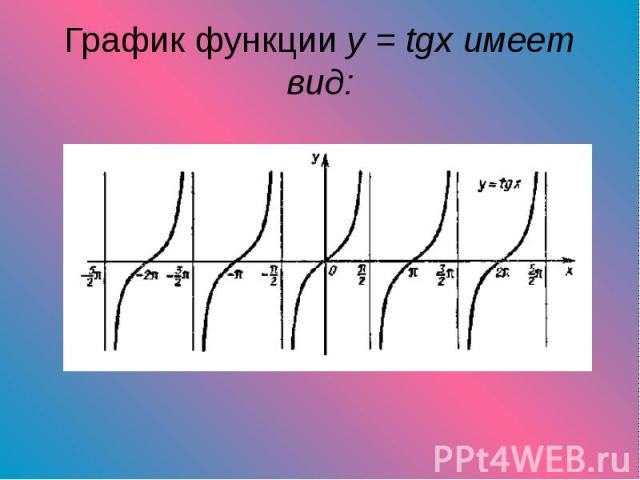
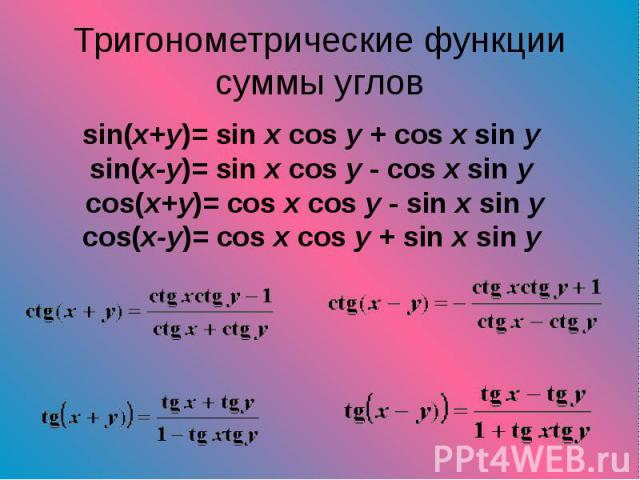Презентация на тему: Примеры тригонометрических функций

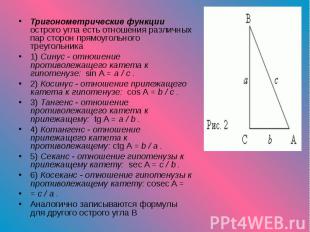
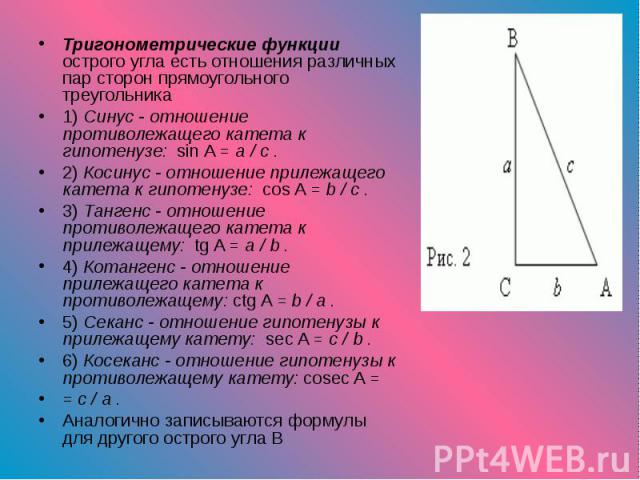
Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника   Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника   1) Синус - отношение противолежащего катета к гипотенузе:  sin A = a / c .   2) Косинус - отношение прилежащего катета к гипотенузе:  cos A = b / c . 3) Тангенс - отношение противолежащего катета к прилежащему:  tg A = a / b . 4) Котангенс - отношение прилежащего катета к противолежащему: ctg A = b / a . 5) Секанс - отношение гипотенузы к прилежащему катету:  sec A = c / b . 6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A = = c / a . Аналогично записываются формулы для другого острого угла B  

П р и м е р :  П р и м е р :  Прямоугольный треугольник ABC  ( рис.2 ) имеет катеты:                          a = 4,  b = 3. Найти синус, косинус и тангенс угла A.   Р е ш е н и е .  Во-первых, найдём гипотенузу, используя теорему Пифагора:                            c 2 = a2 + b 2 , Согласно вышеприведенным формулам имеем: sin A = a / c = 4 / 5  cos A = b / c = 3 / 5  tg A = a / b = 4 / 3 

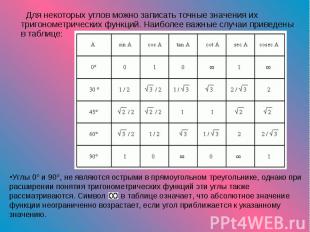
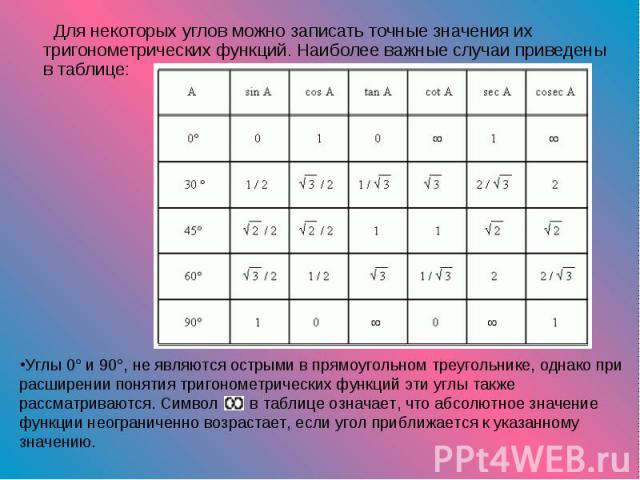
Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице: Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице:

sin 2x = 2 sinx cosx sin 2x = 2 sinx cosx cos 2x = cos2x - sin2x tg 2x = 2 tg x /(1- tg2x) ctg 2x = ctg2x-1/(2 ctg x)

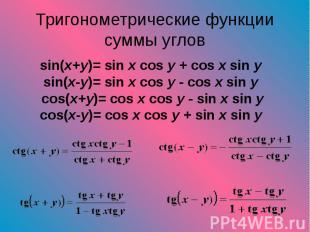
sin(x+y)= sin x cos y + cos x sin y sin(x+y)= sin x cos y + cos x sin y sin(x-y)= sin x cos y - cos x sin y cos(x+y)= cos x cos y - sin x sin y cos(x-y)= cos x cos y + sin x sin y

Для больших значений аргумента можно пользоваться так называемыми формулами приведения, которые позволяют выразить Т. ф. любого аргумента через Для больших значений аргумента можно пользоваться так называемыми формулами приведения, которые позволяют выразить Т. ф. любого аргумента через Т. ф. аргумента x, что упрощает составление таблиц Т. ф. и пользование ими, а также построение графиков. Эти формулы имеют вид:

Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т. ф. суммы или разности значений аргумента через Т. ф. этих значений: Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т. ф. суммы или разности значений аргумента через Т. ф. этих значений: знаки в левой и правой частях всех формул согласованы, то есть верхнему (нижнему) знаку слева соответствует верхний (нижний) знак справа. Из них, в частности, получаются формулы для Т. ф. кратных аргументов, например:

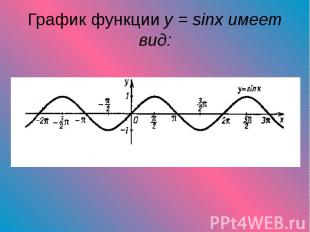
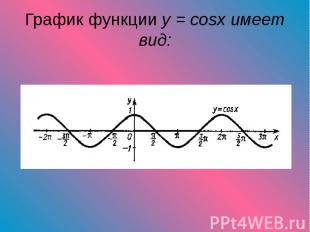
Т. ф. возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу Т. ф., встречаются уже в 3 в. до н. э. в работах математиков Древней Греции - Евклида, Архимеда, Аполлония Пергского и др. Однако эти соотношения не являются у них самостоятельным объектом исследования, так что Т. ф. как таковые ими не изучались. Т. ф. рассматривались первоначально как отрезки и в такой форме применялись Аристархом (конец 4 - 2-я половина 3 вв. до н. э.) Т. ф. возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу Т. ф., встречаются уже в 3 в. до н. э. в работах математиков Древней Греции - Евклида, Архимеда, Аполлония Пергского и др. Однако эти соотношения не являются у них самостоятельным объектом исследования, так что Т. ф. как таковые ими не изучались. Т. ф. рассматривались первоначально как отрезки и в такой форме применялись Аристархом (конец 4 - 2-я половина 3 вв. до н. э.)

Гиппархом (2 в. до н. э.), Менелаем (1 в. н. э.) и Птолемеем (2 в. н. э.) при решении сферических треугольников. Птолемей составил первую таблицу хорд для острых углов через 30' с точностью до 10-6. Разложение Т. ф. в степенные ряды получено И. Ньютоном (1669). В современную форму теорию Т. ф. привёл Л. Эйлер (18 в.). Ему принадлежат определение Т. ф. для действительного и комплексного аргументов, принятая ныне символика, установление связи с показательной функцией, ортогональности системы синусов и косинусов Гиппархом (2 в. до н. э.), Менелаем (1 в. н. э.) и Птолемеем (2 в. н. э.) при решении сферических треугольников. Птолемей составил первую таблицу хорд для острых углов через 30' с точностью до 10-6. Разложение Т. ф. в степенные ряды получено И. Ньютоном (1669). В современную форму теорию Т. ф. привёл Л. Эйлер (18 в.). Ему принадлежат определение Т. ф. для действительного и комплексного аргументов, принятая ныне символика, установление связи с показательной функцией, ортогональности системы синусов и косинусов