![Опр. Пусть функция f задана на отрезке [a,b] и имеет на нем первообразную F. Разность F(b)-F(a) называют определенным интегралом функции f по отрезку [a,b] и обозначают:](https://fs1.ppt4web.ru/images/95232/129815/640/img5.jpg "Опр. Пусть функция f задана на отрезке [a,b] и имеет на нем первообразную F. Разность F(b)-F(a) называют определенным интегралом функции f по отрезку [a,b] и обозначают:")
Презентация на тему: Применение определённого интеграла
Применение определенного интеграла
Цель: Изучение определенного интеграла и его применение.
Задачи: проанализировать научную и методическую литературу по данной теме; рассмотреть понятие определенного интеграла; рассмотреть практическое применение интегралов в физике и геометрии; провести сравнительный анализ наиболее распространенных в средней школе учебных пособиях; разработать факультативный курс по теме «Применение определенного интеграла».
Содержание: Введение. Гл. 1. Неопределенные и определенные интегралы. §1. Неопределенный интеграл, его свойства. §2. Методы интегрирования. §3. Определенный интеграл. §4. Свойства определенного интеграла. Гл. 2. Различные подходы теории интеграла в учебных пособиях для школьников. §1. Вводные замечания. §2. Суммы Дарбу. §3. Интегральная сумма. §4. Свойство разности значений первообразной. §5. Оценка разности S-s. §6. Остальные результаты §7.Анализ изложения темы «Определенный интеграл» в современных учебниках.
Гл.3. Применение определенного интеграла. §1. Вычисление длины кривой. §2. Точное определение понятия площади плоской фигуры. §3. Площадь трапеции, выраженная интегралом. §4. Определение объема тела. §5. Объем тела вращения. §6. Нахождение статических моментов и центра тяжести кривой. §7. Нахождение статических моментов и центра тяжести плоской фигуры. §8. Механическая работа. Гл. 4. Разработка факультатива по теме «Определенный интеграл». Заключение. Список литературы.
![Опр. Пусть функция f задана на отрезке [a,b] и имеет на нем первообразную F. Раз](https://fs1.ppt4web.ru/images/95232/129815/310/img5.jpg "Опр. Пусть функция f задана на отрезке [a,b] и имеет на нем первообразную F. Раз")
Опр. Пусть функция f задана на отрезке [a,b] и имеет на нем первообразную F. Разность F(b)-F(a) называют определенным интегралом функции f по отрезку [a,b] и обозначают:
Подходы к построению теории интеграла: предел интегральных сумм; приращение первообразной; единственное число, расположенное между нижними и верхними суммами Дарбу.
Формула объема тела через площадь сечений: Формула объема тела вращения: Формула вычисления механической работы:
Факультатив «Применение определенного интеграла» Разработан для 11 классов. Состоит из 6 уроков по 40 минут. Цели: повышение интереса учащихся к предмету; расширение и углубление знаний; развитие мышление; повторение данной темы перед вступительными экзаменами и ЕГЭ.
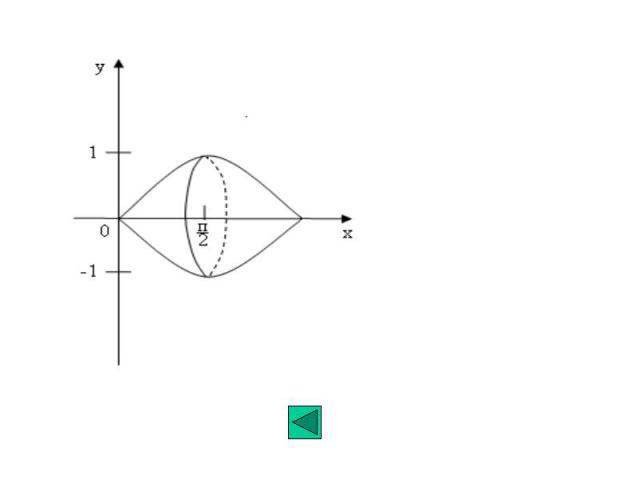
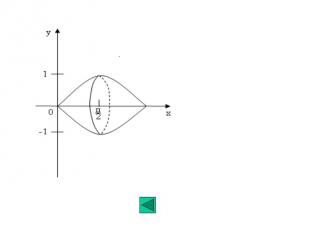
Пример. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды Решение: Воспользуемся формулой для вычисления объема тела вращения получаем далее вычисляется данный интеграл:
