X
Код для использования на сайте:
Презентация на тему: "Вычисление площадей плоских фигур с помощью определенного интеграла"
Презентации по предмету
Презентация на тему: "Вычисление площадей плоских фигур с помощью определенного интеграла"
№ слайда 1


Описание слайда:
№ слайда 2

Описание слайда:
№ слайда 3

Описание слайда:
№ слайда 4


Описание слайда:
№ слайда 5


Описание слайда:
«Интеграл» придумал Якоб Бернулли (1690г.) «Интеграл» придумал Якоб Бернулли (1690г.) «восстанавливать» от латинского integro «целый» от латинского integer
№ слайда 6


Описание слайда:
Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга.
№ слайда 7


Описание слайда:
№ слайда 8


Описание слайда:
№ слайда 9


Описание слайда:
И. Ньютон И. Ньютон
№ слайда 10

Описание слайда:
№ слайда 11


Описание слайда:
№ слайда 12


Описание слайда:
y = 3 – x2, y = 3 – x2, y = 1+ | x |
№ слайда 13
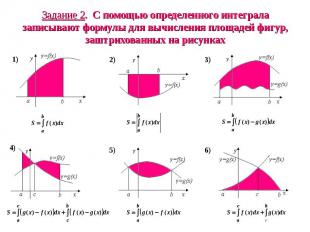

Описание слайда:
№ слайда 14


Описание слайда:
№ слайда 15
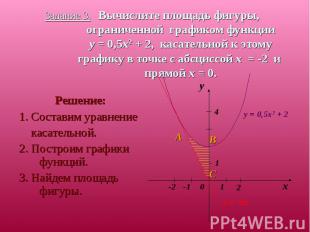

Описание слайда:
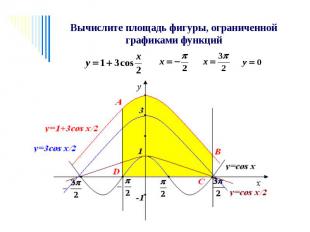
Решение: Решение: 1. Составим уравнение касательной. 2. Построим графики функций. 3. Найдем площадь фигуры.
№ слайда 16


Описание слайда:
№ слайда 17


Описание слайда:
Презентации из категории
Лучшее на fresher.ru