Презентация на тему: Производная

Производная

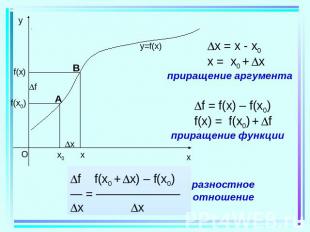
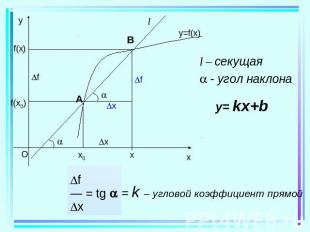
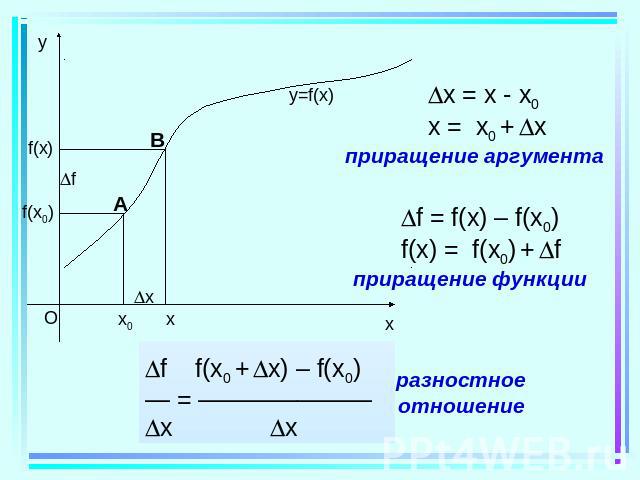
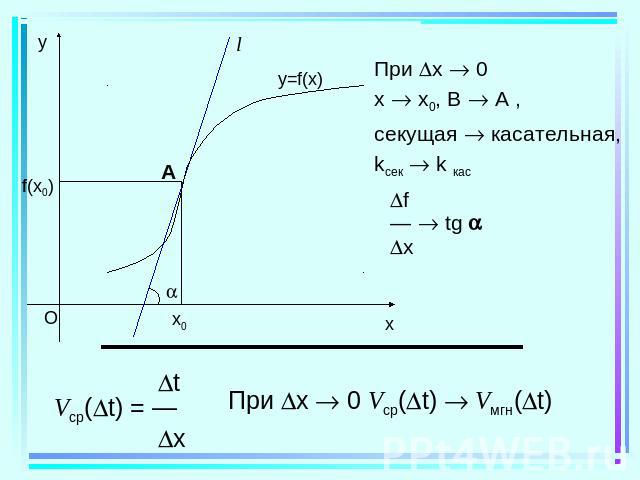
Если тело движется по прямой и за время t его координата изменяется на x, то- средняя скорость движения тела за t

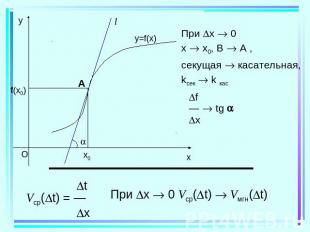
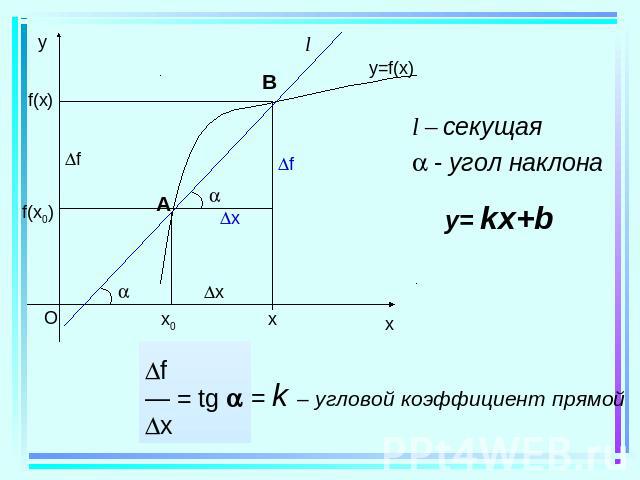
Производная Производной функции f в точке x0 называется число, к которому стремится разностное отношение при x 0. f f(x0 + x) – f(x0)f´(x0)= — = ——————— x x при x 0.

Правила вычисления производных Если функции U и V дифференцируемы в точке x0, тоЕсли функция U дифференцируема в точке x0, а С-постоянная, то (СU)´=CU´Если функции U и V дифференцируемы в точке x0, то( U + V )´ = U´ + V´(U V)´ = U´ V + U V´ U ´ U´ V - U V´ — = —————— V V2Если функция U дифференцируема в точке x0, а С-постоянная, то (СU)´=CU´

Формулы для вычисления производных C´ = 0 x´ = 1 (xn)´= nxn-1 1 (x)´= —— 2 x5. 1 ´ 1 — = - —— x x2

Задание 1. Найдите производные функций:f(x)=3x+52. f(x)=4x2-5x3+9x 3 x3. f(x)= — + — x 3 2 5 74. f(x) = — + — - — x2 x3 x 5. f(x)= x + 4 1 1 6. f(x) = — + — + 4x 3x 2x2

Задание 2. Найдите производные функций:1. f(x)=(3x+5)(x-3)2. f(x)=(x2-5x)(x3-x2) 3 + x3. f(x)= —— x3 2x2 - 54. f(x) = ——— x + 15. f(x)= (x + 4) (x - 2) 1 1 6. f(x) = — + — 4x2 2 x

Ответы: 1. f´(x)=32. f´(x)=8x-15x2+x 3 13. f´(x)= - — + — x2 3 4 15 74. f´(x) = - — - — + — x3 x4 x2 5. f´(x)= 1/(2x) 1 1 6. f´(x) = - — - — + 1/x 3x2 2x3 1. f´(x)=6x-92. f´(x)=5x4-24x3+15x2 4x+93. f´(x)= —— x4 2x2+4x+54. f´(x) = ———— (x+1)2 5. f´(x)= 1+1/x6. f´(x) = 4x+4