Презентация на тему: Приращение аргумента. Приращение функции

МБОУ лицей №10 города СоветскаКалининградской области учитель математикиРазыграева Татьяна НиколаевнаПриращение аргумента.Приращение функции.

При сравнении значения функции f в некоторой фиксированной точке x₀ со значениями этой функции в различных точках x, лежащих в окрестности x₀, удобно выражать разность f(x) – f(x₀) через разность x – x₀, пользуясь понятиями «приращение аргумента» и «приращение функции».Пусть x – произвольная точка, лежащая в некоторой окрестности фиксированной точки x₀. Разность x – x₀ называется приращением независимой переменной ( или приращением аргумента) в точке x₀ и обозначается Δx. Таким образом,

Говорят также, что первоначальное значение аргумента x₀ получило приращение Δx. Вследствие этого значение функции f изменится на величину f(x) – f(x₀) = f (x₀ +Δx) – f(x₀).Эта разность называется приращением функции f в точке x₀, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению

При фиксированном x₀ приращение Δf есть функция от Δx. Δf называют также приращением зависимой переменной и обозначают через Δy для функции y = f(x) .Найти приращение функции функции у = х² при переходе от точки х₀ = 1 к точкам : а) х = 1,1; б) х = 0,98

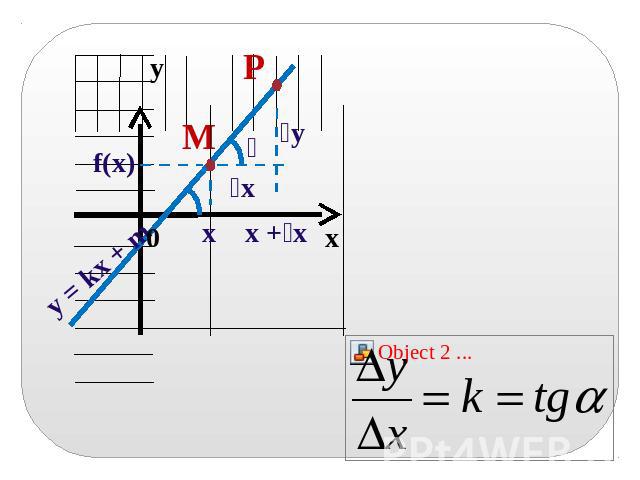
Функция y = f(x) непрерывна в точке х = а, если в точке х = а выполняется следующее условие: если х 0, то у 0.Для функции y = kx + m найти: а) приращение функции при переходе от фиксированной точки х к точке х + х; б) предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Имеем:f(x) = kx + m f(x + x) = k(x + x) + m y = f(x + x) – f(x) = (k(x + x) + m) – (kx + m) y = (kx + kx + m) – (kx + m) = k·x.

Пример № 3.Для функции y = x² найти: а) приращение функции при переходе от фиксированной точки х к точке х + х; б) предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю.

Итак, для заданной функции y = x² получили: