Презентация на тему: Применение производной к исследованию функций

Применение производной к исследованию функций презентация учителя математики Верхнегерасимовской СШ І-ІІІ ступеней Горбань Натальи Геннадиевны

Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики.

Используя методы дифференциального исчисления английский астроном, математик Эдмон Галлей ещё в XVII веке предсказал возвращение кометы Галлея. В 1705 году Эдмонд Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году (что, увы, было уже после его смерти). Комета действительно возвратилась, как было предсказано, и позже была названа в его честь. Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.

Разминка Найти производную функции

Признак возрастания и убывания функции

По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая из функций определена на R

По графику производной функции определите промежутки возрастания и промежутки убывания функции

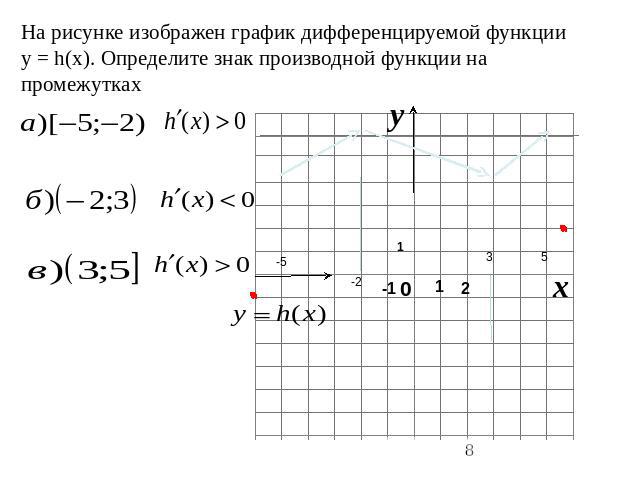
На рисунке изображен график дифференцируемой функции y = h(x). Определите знак производной функции на промежутках

Укажите критические точки функции , используя график производной функции .

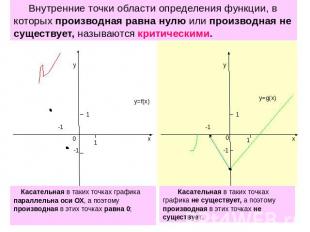
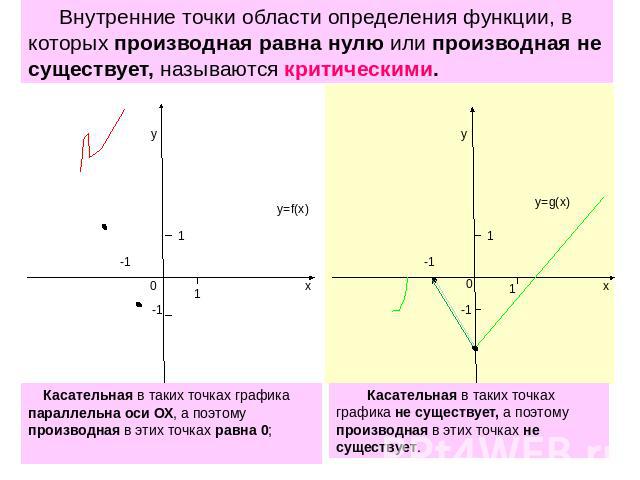
Внутренние точки области определения функции, в которых производная равна нулю или производная не существует, называются критическими. Касательная в таких точках графика параллельна оси ОХ, а поэтому производная в этиКасательная в таких точках графика не существует, а поэтому производная в этих точках не существует.х точках равна 0;

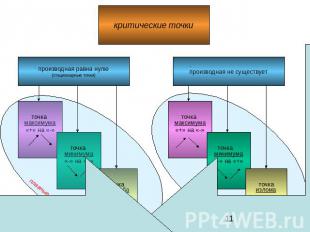
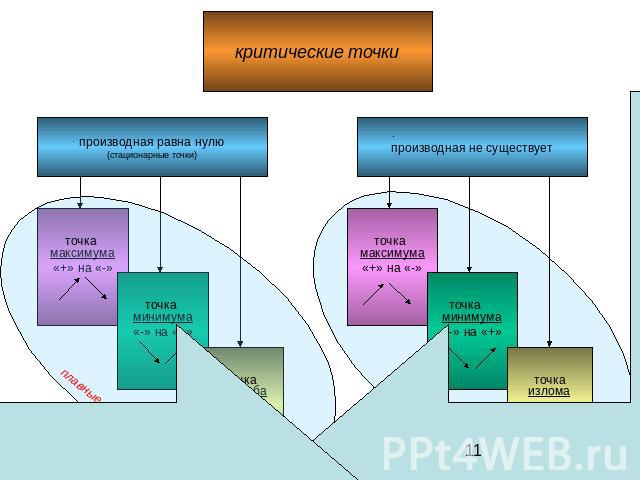
критические точки

Достаточное условие существования экстремума функции: Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «+» на «-», то х0 – точка максимума функции f(x). Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).3) Если при переходе через критическую точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.

Исследование функций с помощью производной и построение графиков функций.

Схема исследования функции Найти область определения функции;Исследовать функцию на четность, нечетность, периодичность;Найти точки пересечения графика функции с осями координат;Исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;Найти точки экстремума и экстремальные значения функции;Построить график функции.

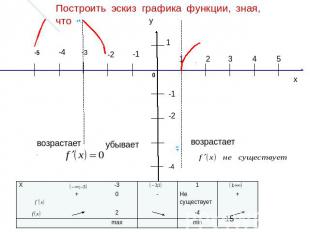
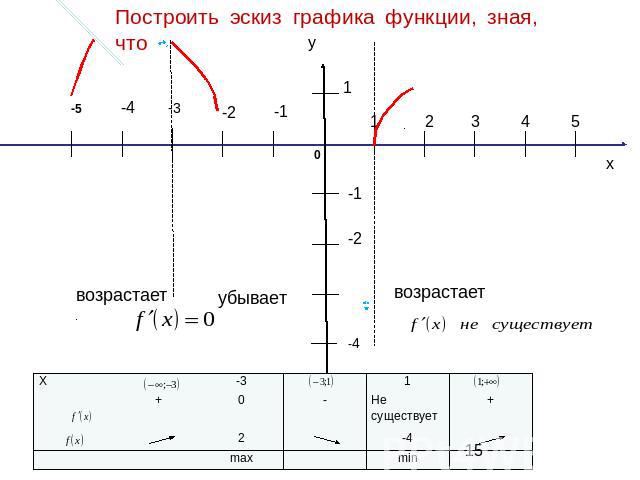
Построить эскиз графика функции, зная, что

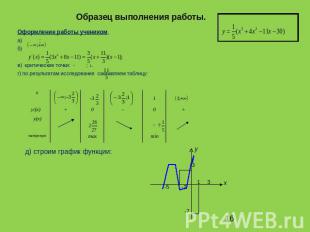
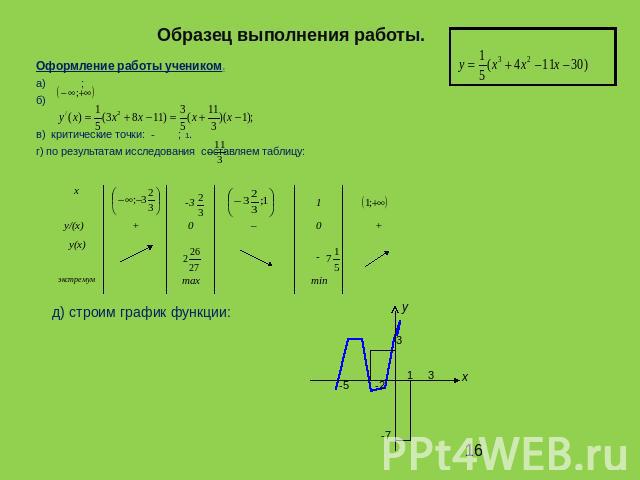
Образец выполнения работы.

Задачи на нахождение наибольшего и наименьшего значений

Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b] Чтобы найти наибольшее и наименьшее значения непрерывной функции f(x) на промежутке [a;b], нужно вычислить её значения f(a) и f(b) на концах данного промежутка вычислить её значения в критических точках, принадлежащих этому промежутку выбрать из них наибольшее и наименьшее.Записывают так: max f(x) и min f(x) [a;b] [a;b]