Презентация на тему: Применение производной к исследованию функций

Применение производной к исследованию функций 2 курс

Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, и умение. А.Н. Крылов (Русский советский математик, кораблестроитель, академик )

Математическим выражением взаимной связи реальных величин является идея функциональной зависимости. Понятие функции – важнейшее понятие математики. Слово «функция» (от латинского «Functio» - исполнение обязанностей, деятельность) впервые ввел немецкий ученый Г. Лейбниц.

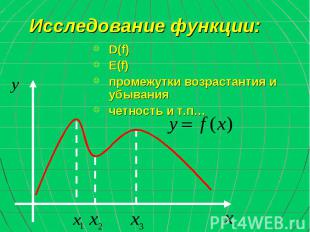
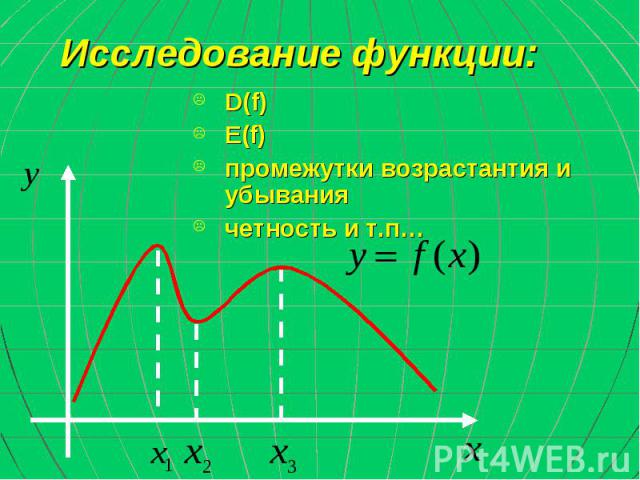
Исследование функции: D(f) E(f) промежутки возрастантия и убывания четность и т.п…

далее Повторение Четность, нечетность функций Периодичность Нули функции Промежутки знакопостоянства Монотонность функции

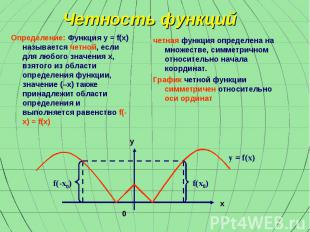
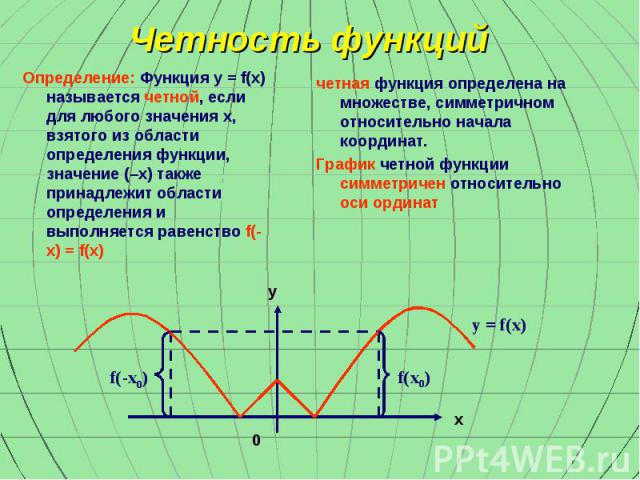
f(x0) f(-x0) y = f(x) у х 0 Четность функций Определение: Функция y = f(x) называется четной, если для любого значения x, взятого из области определения функции, значение (–x) также принадлежит области определения и выполняется равенство f(-x) = f(x) четная функция определена на множестве, симметричном относительно начала координат. График четной функции симметричен относительно оси ординат

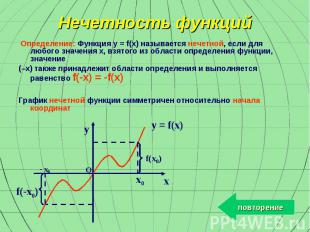
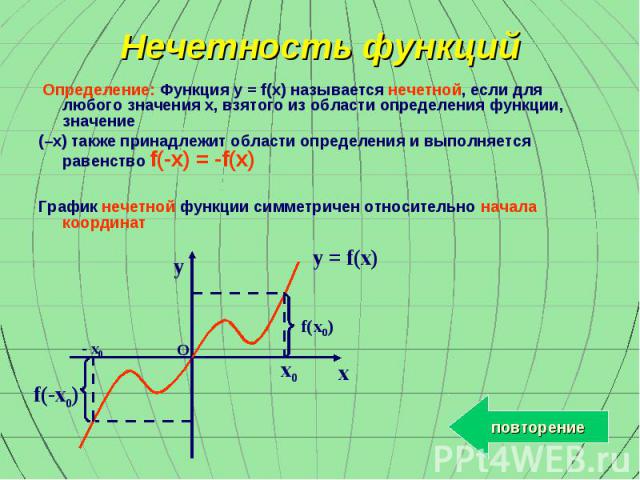
y x x0 - x0 f(x0) f(-x0) O y = f(x) Нечетность функций Определение: Функция y = f(x) называется нечетной, если для любого значения x, взятого из области определения функции, значение (–x) также принадлежит области определения и выполняется равенство f(-x) = -f(x) График нечетной функции симметричен относительно начала координат повторение

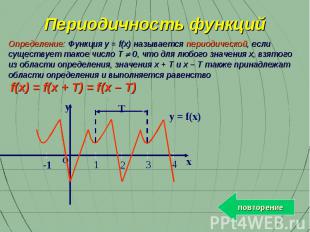
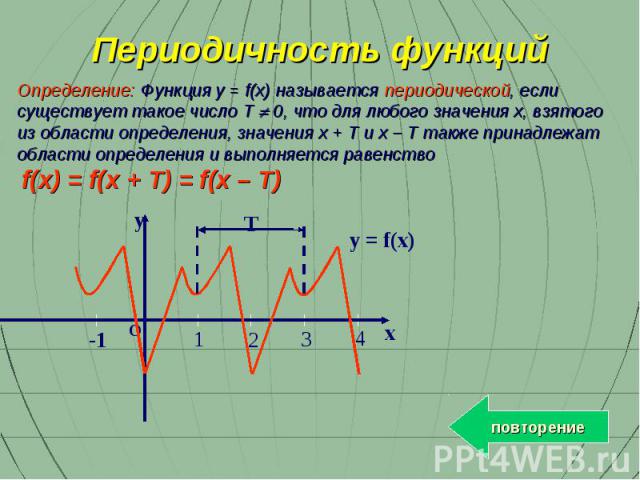
Определение: Функция y = f(x) называется периодической, если существует такое число T 0, что для любого значения x, взятого из области определения, значения x + T и x – T также принадлежат области определения и выполняется равенство f(x) = f(x + T) = f(x – T) y 1 2 4 3 -1 x O T y = f(x) Периодичность функций повторение

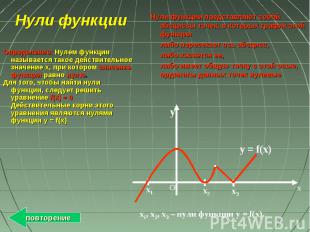
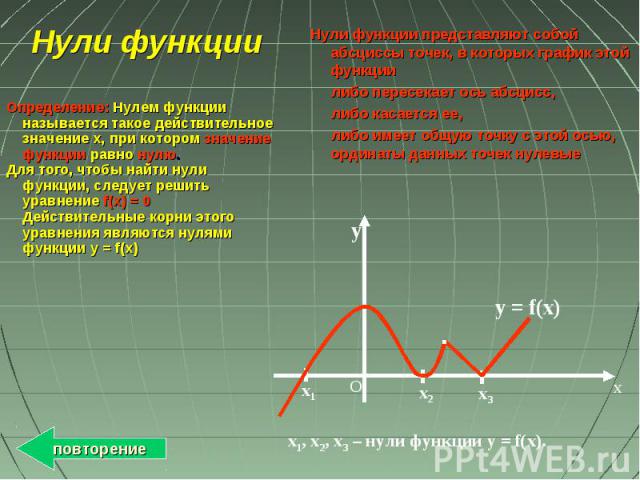
x y O x1 x3 x2 y = f(x) х1, х2, х3 – нули функции у = f(x). Нули функции Определение: Нулем функции называется такое действительное значение x, при котором значение функции равно нулю. Для того, чтобы найти нули функции, следует решить уравнение f(x) = 0 Действительные корни этого уравнения являются нулями функции y = f(x) Нули функции представляют собой абсциссы точек, в которых график этой функции либо пересекает ось абсцисс, либо касается ее, либо имеет общую точку с этой осью, ординаты данных точек нулевые повторение

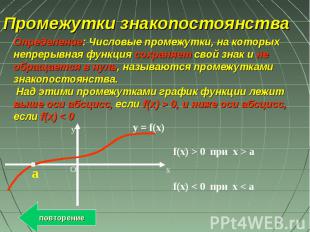
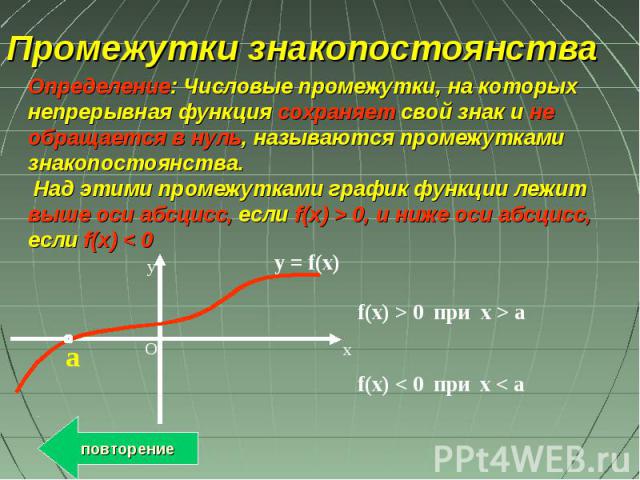
Промежутки знакопостоянства Определение: Числовые промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства. Над этими промежутками график функции лежит выше оси абсцисс, если f(x) > 0, и ниже оси абсцисс, если f(x) < 0 O y x y = f(x) a f(x) > 0 при x > a f(x) < 0 при x < a повторение

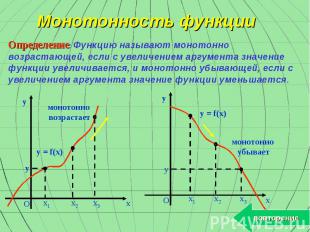
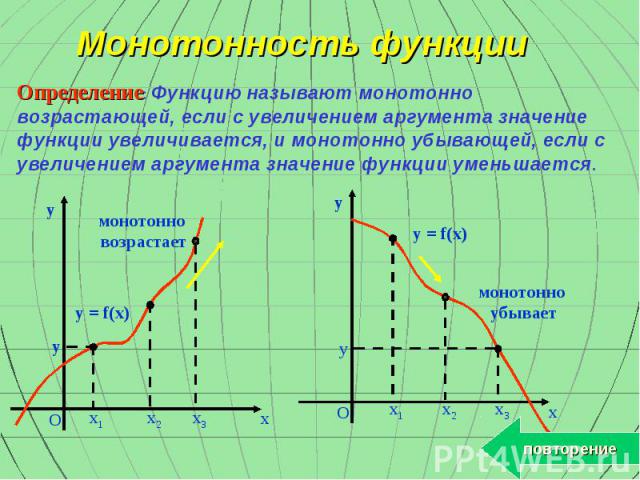
Монотонность функции Определение: Функцию называют монотонно возрастающей, если с увеличением аргумента значение функции увеличивается, и монотонно убывающей, если с увеличением аргумента значение функции уменьшается. y x O y x3 x2 x1 монотонно возрастает y = f(x) y x O y = f(x) монотонно убывает y x3 x2 x1 повторение

Связь производной с монотонностью функции Если производная функции в каждой точке некоторого промежутка положительна, то функция на этом промежутке возрастает, т.е.f’(x)>0, f(x) Если производная функции в каждой точке некоторого промежутка отрицательна, то функция на этом промежутке убывает, т.е.f’(x)

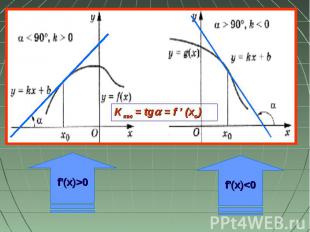
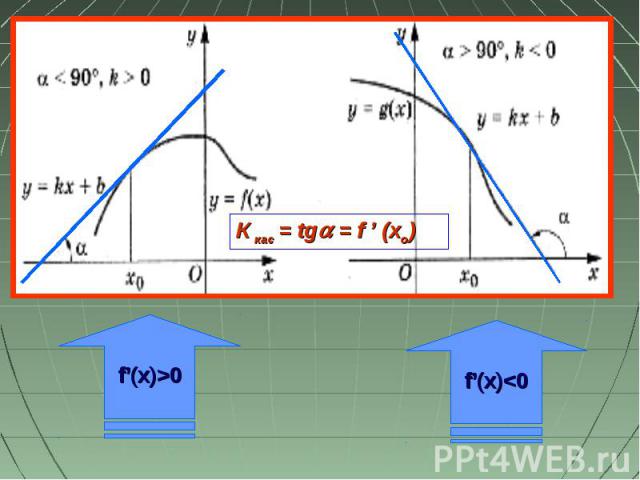
f’(x)>0 f’(x)

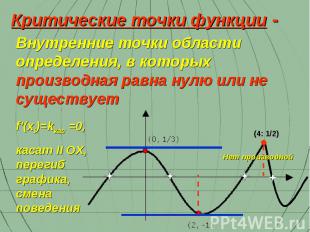
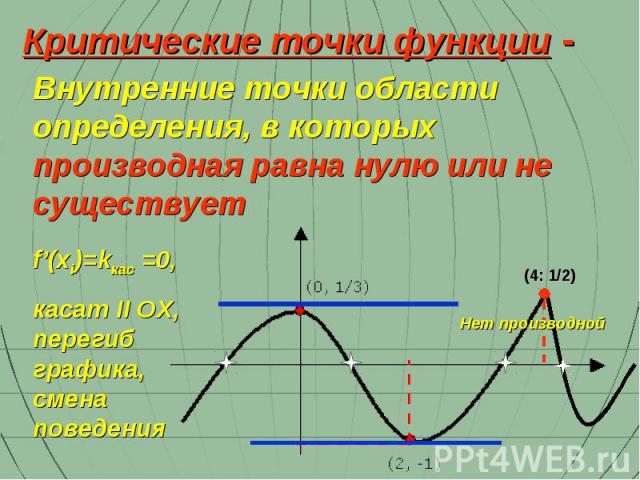
Внутренние точки области определения, в которых производная равна нулю или не существует Критические точки функции - (4: 1/2) f’(xi)=kкас =0, касат II OX, перегиб графика, смена поведения Нет производной

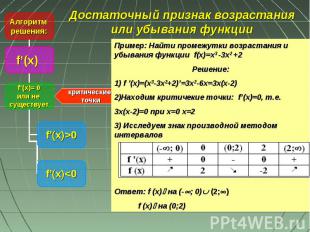
Алгоритм решения: f’(х) f’(х)= 0 или не существует f’(x)>0 f’(x)

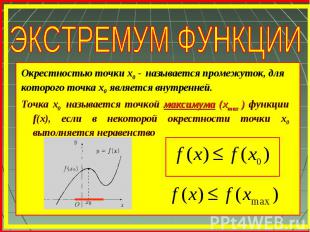
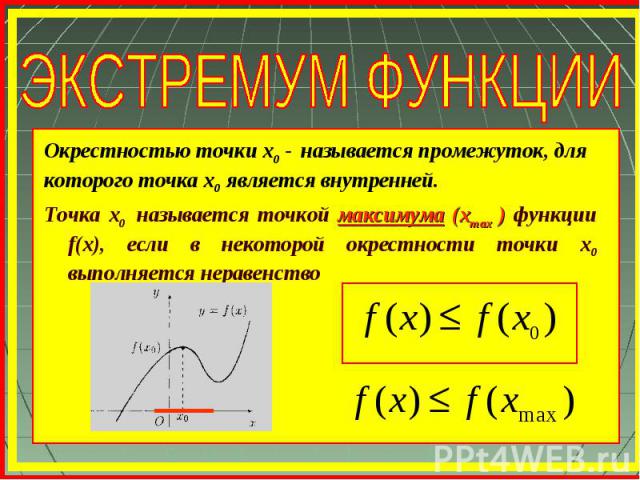
Точка х0 называется точкой максимума (xmax ) функции f(x), если в некоторой окрестности точки х0 выполняется неравенство Окрестностью точки х0 - называется промежуток, для которого точка х0 является внутренней.

Точка х1 называется точкой минимума (xmin ) функции f(x), если в некоторой окрестности точки х1 выполняется неравенство Точки минимума и максимума называются точками экстремума (крайние, конечные) Значения функции в точках х0 и х1 называются соответственно максимумом и минимумом функции (ymin и ymax) Максимум и минимум функции называется экстремумом функции

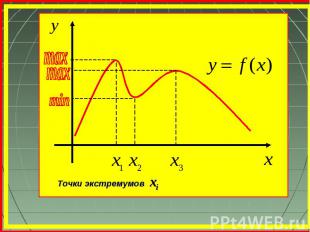
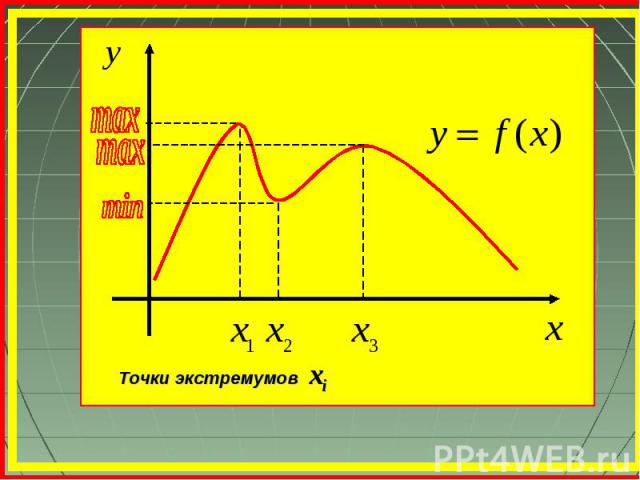
Точки экстремумов хі

Обратите внимание!!! Что происходит с производной при переходе через экстремальную точку? Что происходит с самой функцией при переходе через экстремальную точку?