Презентация на тему: Применение производной к исследованию функций

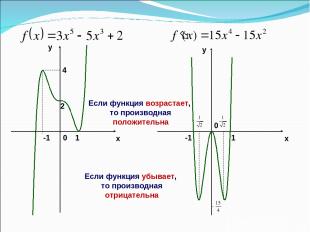
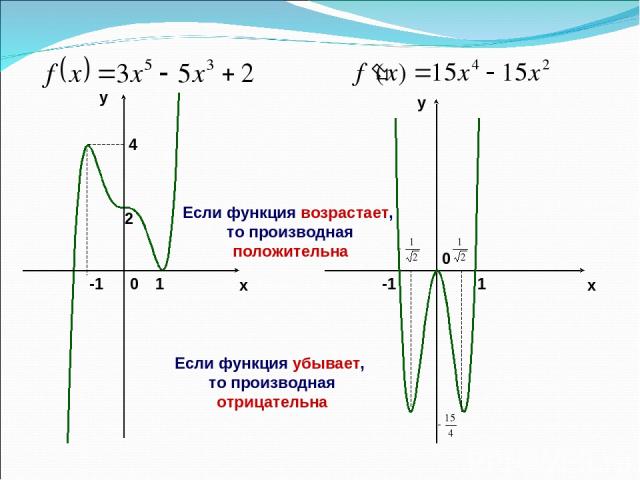
x y y x 2 -1 1 4 0 -1 1 0 Если функция возрастает, то производная положительна Если функция убывает, то производная отрицательна

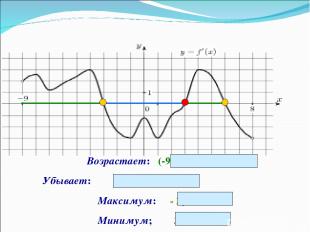
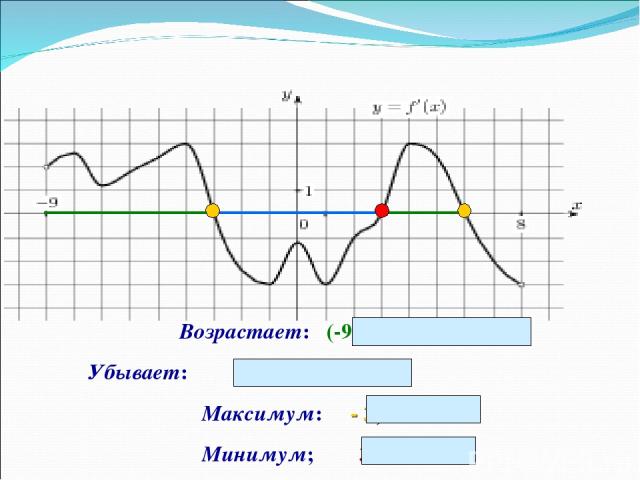
Максимум: - 3; 6 Минимум; 3 Возрастает: (-9;-3) и (3;6) Убывает: (-3;3)

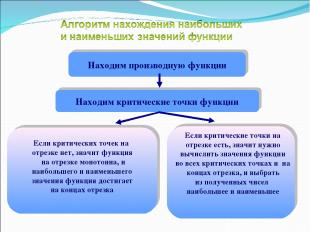
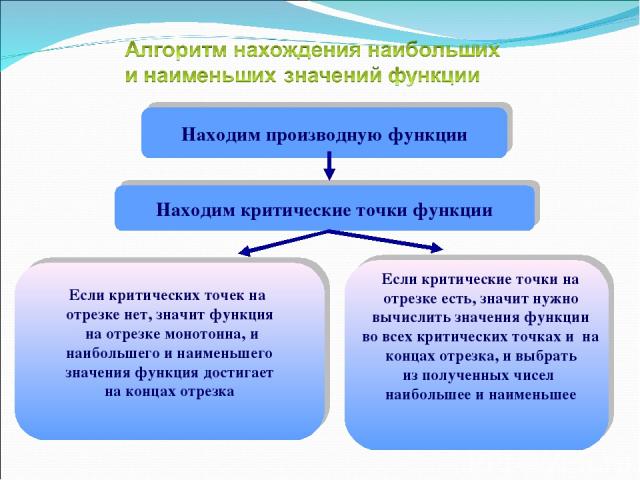
Находим производную функции Находим критические точки функции Если критических точек на отрезке нет, значит функция на отрезке монотонна, и наибольшего и наименьшего значения функция достигает на концах отрезка Если критические точки на отрезке есть, значит нужно вычислить значения функции во всех критических точках и на концах отрезка, и выбрать из полученных чисел наибольшее и наименьшее

х = 1 ; х = 5/3 f(-1)=18 f(3) = 2 f(1) = 6 f(5/3) = 55/9 max f(x)=f(-1)=18 [-1;3] min f(x)=f(3)=2 [-1;3] ответ Решение:

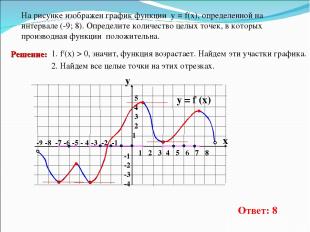
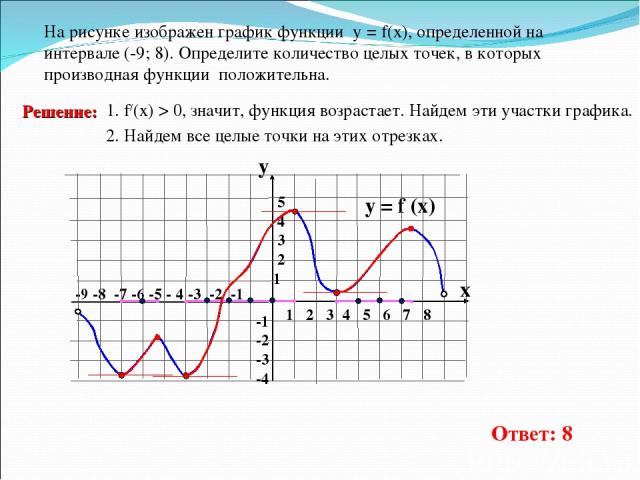
-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции  положительна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 8 Решение:

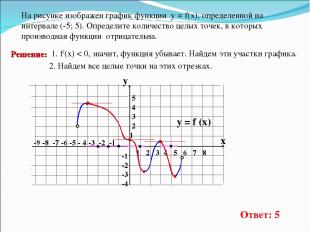
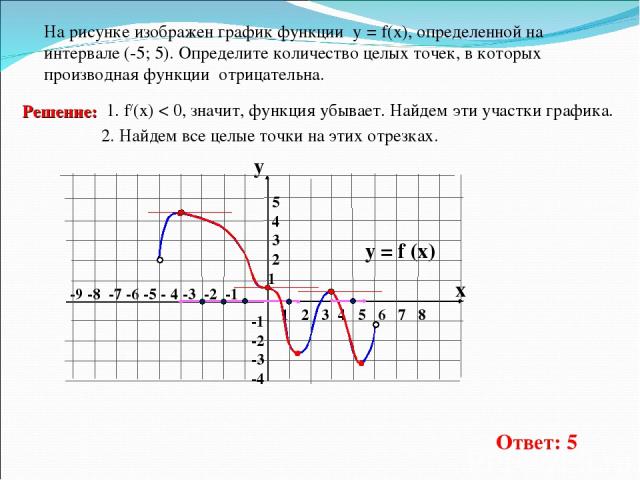
-9 -8 -7 -6 -5 - 4 -3 -2 -1 1 2 3 4 5 6 7 8 На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции  отрицательна. y = f (x) y x 5 4 3 2 1 -1 -2 -3 -4 1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика. 2. Найдем все целые точки на этих отрезках. Ответ: 5 Решение:

Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f(x)   y x Ответ: 5 a b

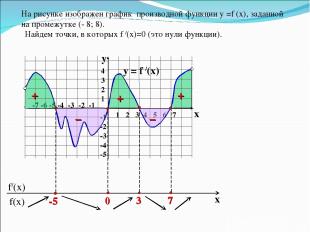
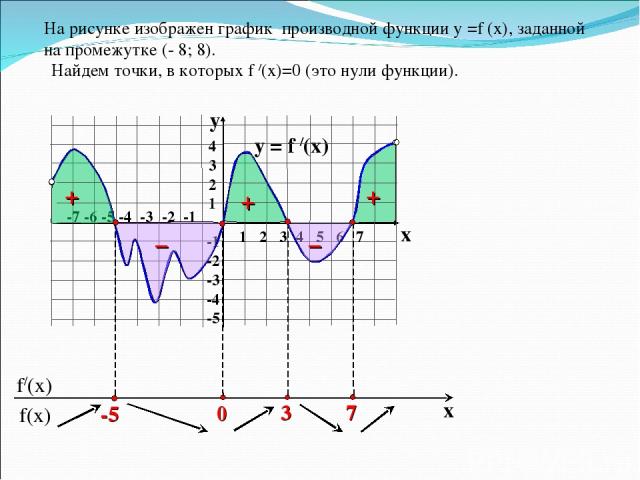
На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). y = f /(x)   1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x Найдем точки, в которых f /(x)=0 (это нули функции). + – – + +

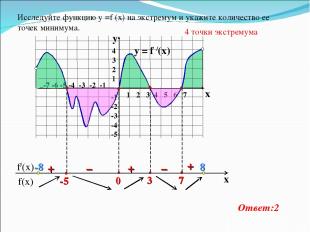
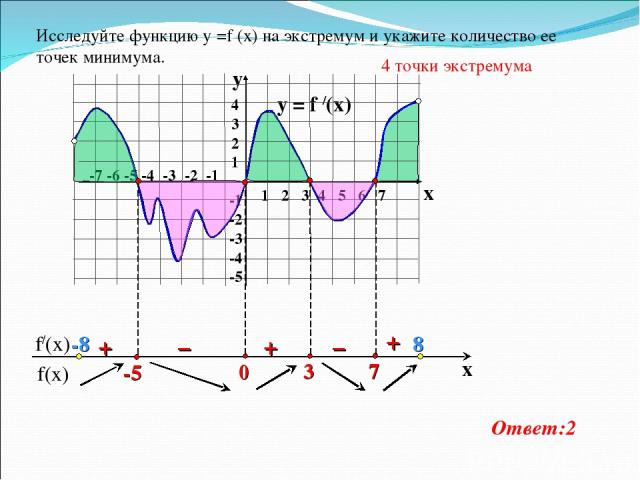
y = f /(x)   1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума. 4 точки экстремума Ответ:2 -8 8

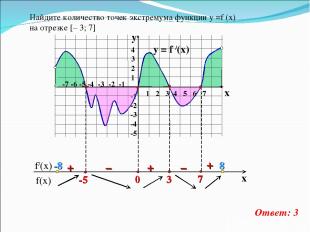
y = f /(x)   4 3 2 1 -1 -2 -3 -4 -5 y x + – – + + Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7] Ответ: 3 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -8 8

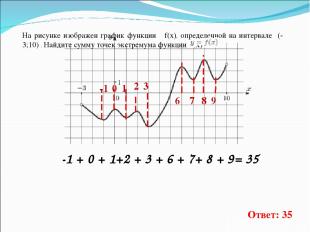
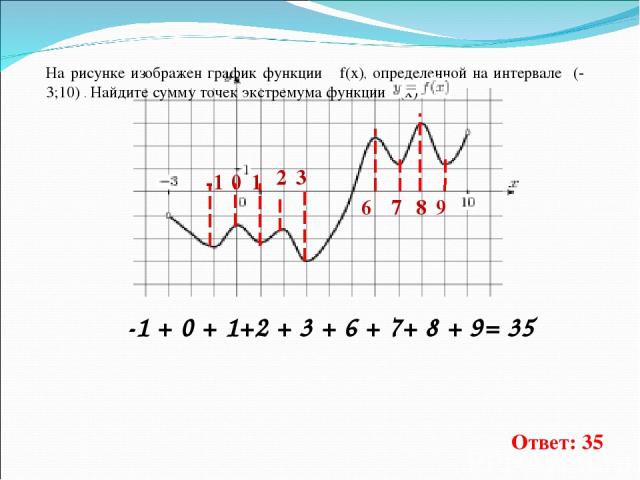
На рисунке изображен график функции f(x), определенной на интервале (-3;10) . Найдите сумму точек экстремума функции f(x) . -1 0 1 3 6 7 8 9 -1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35 Ответ: 35 2

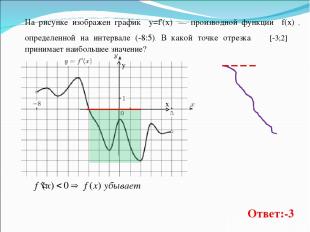
На рисунке изображен график y=f'(x)  — производной функции f(x) , определенной на интервале (-8:5). В какой точке отрезка [-3;2] принимает наибольшее значение? Ответ:-3

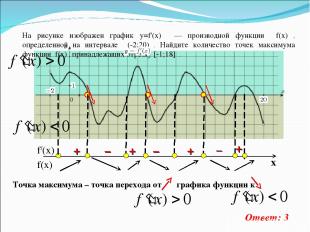
На рисунке изображен график y=f'(x)  — производной функции f(x) , определенной на интервале (-2;20) . Найдите количество точек максимума функции f(x) , принадлежащих отрезку [-1;18] . Ответ: 3 _ – – + + + +

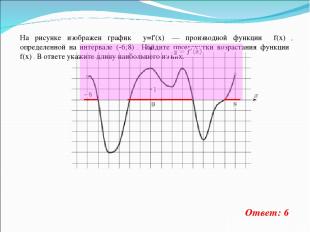
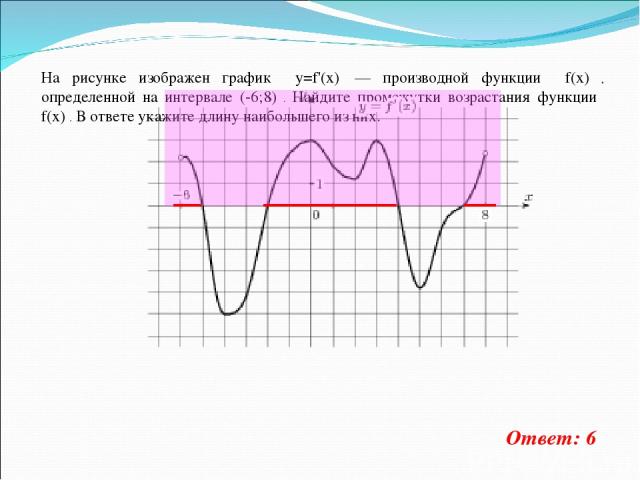
На рисунке изображен график y=f'(x)  — производной функции f(x) , определенной на интервале (-6;8) . Найдите промежутки возрастания функции f(x) . В ответе укажите длину наибольшего из них. Ответ: 6

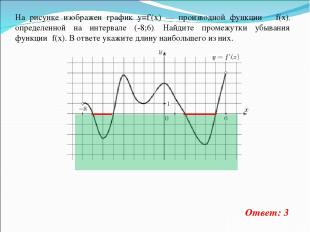
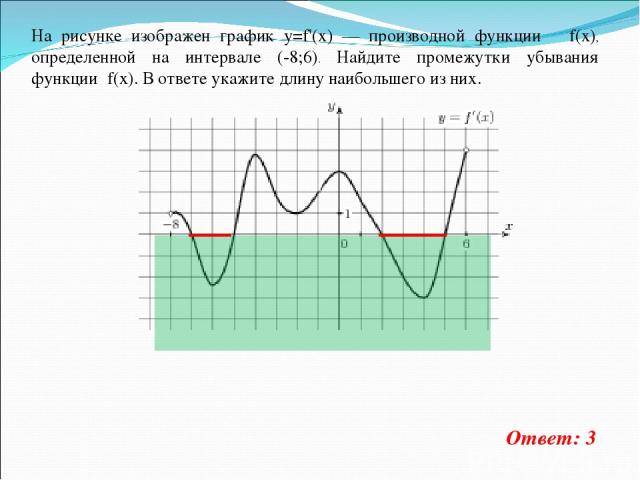
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. Ответ: 3