Презентация на тему: Применение производной к исследованию и построению графиков функций

Областное государственное автономное образовательное учреждениесреднего профессионального образованияБелгородский строительный колледжг. Белгород Урок-лекция «Применение производной к исследованию и построению графиков функций» урок математики, 1 курс Автор: Агапова Наталья Николаевна,преподаватель математики

научиться применять таблицу производных при исследовании функций и построении графиковнаучиться применять таблицу производных при исследовании функций и построении графиков

Математический диктант Вариант 1.(Cu)’=……=(u’v-v’u)/v²(cos x)’=……=1/cos² x(ex)’=…Вариант 2.C’=……=(u’v+v’u)(sin x)’=……=-1/sin² x(xn)’=…Вариант 1.(Cu)’=Cu’(u/v)=(u’v-v’u)/v²(cos x)’=-sin xtg x=1/cos² x(ex)’=exВариант 2.C’=0(uv)’=(u’v+v’u)(sin x)’=cos xctg x=-1/sin² x(xn)’=n*xn-1

Классная работа Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков монотонности функции (промежутков возрастания и убывания). Такой анализ легко сделать с помощью производной.

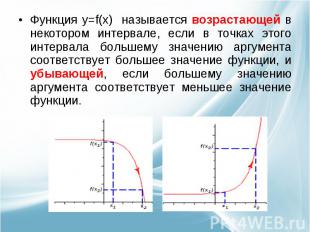
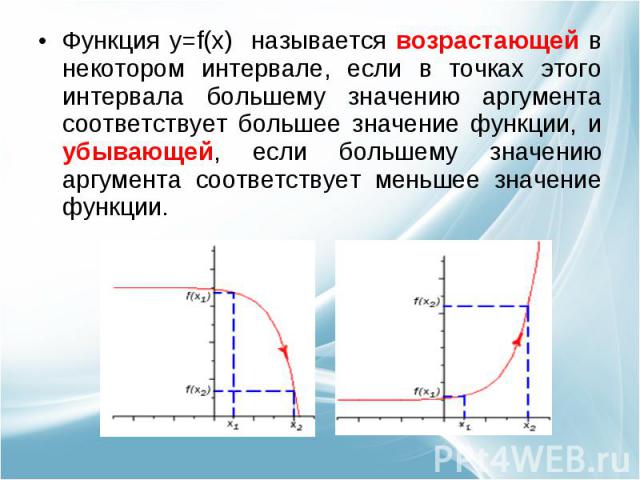
Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.

Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).

Правило нахождения интервалов монотонности Находим область определения функции f(x).Вычисляем производную f’(x) данной функции.Находим точки, в которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.

Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5 Область определения: R. Функция непрерывна.Вычисляем производную : y’=6x²-6x-36.Находим критические точки: y’=0. x²-x-6=0Д=1-4*(-6)*1=1+24=25Делим область определения на интервалы: Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].

Пример №2. Найти промежутки монотонности функции y=x³-3x² Область определения: R. Функция непрерывна.Вычисляем производную : y’=3x²-6x.Находим критические точки: y’=0. x²-2x=0x(x-2)=0x1=0 и x2=2Делим область определения на интервалы: Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].

Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x0).Точку x=x0 называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).

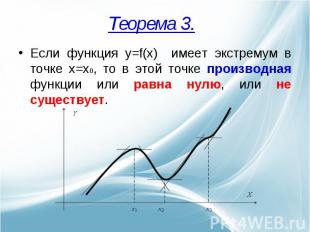
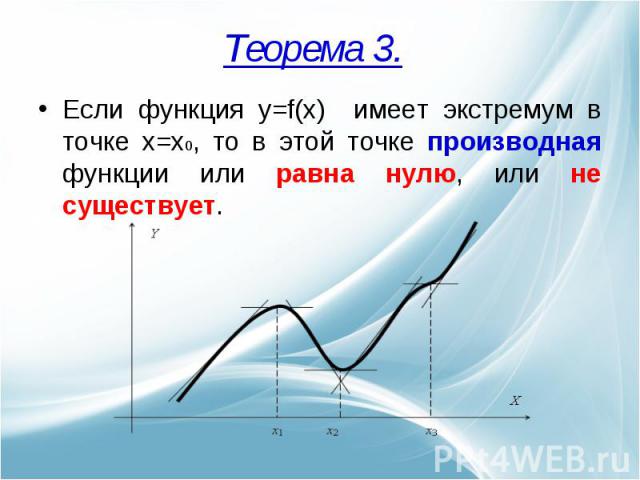
Если функция y=f(x) имеет экстремум в точке x=x0, то в этой точке производная функции или равна нулю, или не существует.

Если производная f’(x) при переходе через точку x0 меняет знак, то точка x0 является точкой экстремума функции f(x).Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума

Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4 Область определения: R. Функция непрерывна.Вычисляем производную : y’=-6x²-6x+12.Находим критические точки: y’=0. -x²-x+2=0Д=1-4*(-1)*2=1+8=9x1=1; x2=-2Делим область определения на интервалы: x=-2 – точка минимума. Найдём минимум функции ymin=-24. x=1 – точка максимума. Найдём максимум функции: ymax=3.

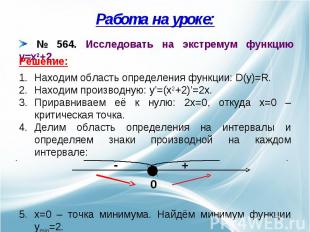
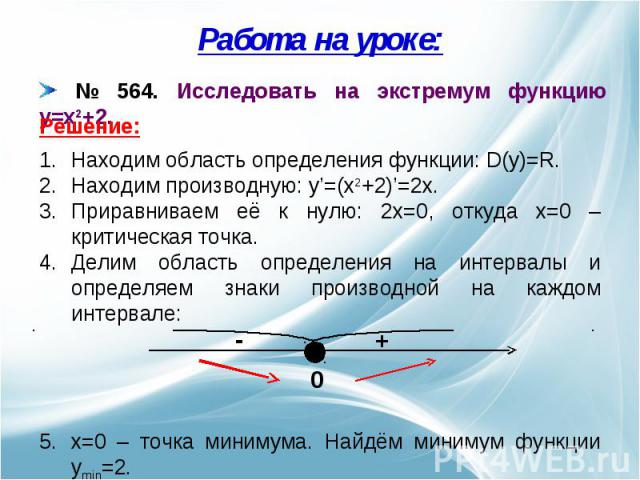
Работа на уроке: № 564. Исследовать на экстремум функцию y=x2+2. Находим область определения функции: D(y)=R.Находим производную: y’=(x2+2)’=2x.Приравниваем её к нулю: 2x=0, откуда x=0 – критическая точка.Делим область определения на интервалы и определяем знаки производной на каждом интервале:x=0 – точка минимума. Найдём минимум функции ymin=2.

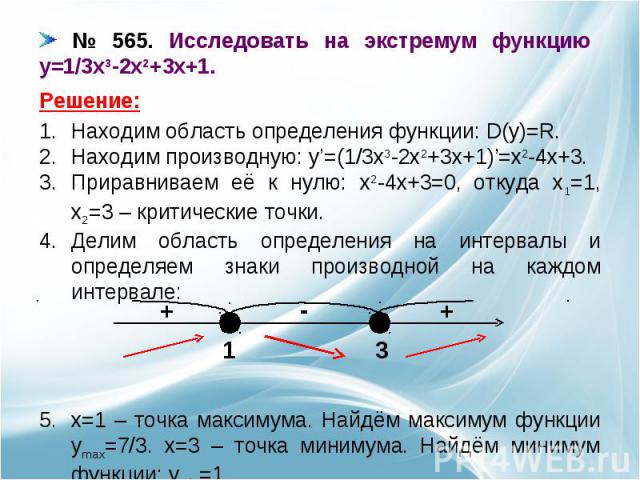
№ 565. Исследовать на экстремум функцию y=1/3x3-2x2+3x+1. Находим область определения функции: D(y)=R.Находим производную: y’=(1/3x3-2x2+3x+1)’=x2-4x+3.Приравниваем её к нулю: x2-4x+3=0, откуда x1=1, x2=3 – критические точки.Делим область определения на интервалы и определяем знаки производной на каждом интервале:x=1 – точка максимума. Найдём максимум функции ymax=7/3. x=3 – точка минимума. Найдём минимум функции: ymin=1.

№ 566. Исследовать на экстремум функцию y=x3+3x2+9x-6. Находим область определения функции: D(y)=R.Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9.Приравниваем её к нулю: 3x2+6x+9=0, откуда D<0. То есть критических точек не существует.Однако, функция возрастает на всей D(y), так как y’=3x2+6x+9 >0:

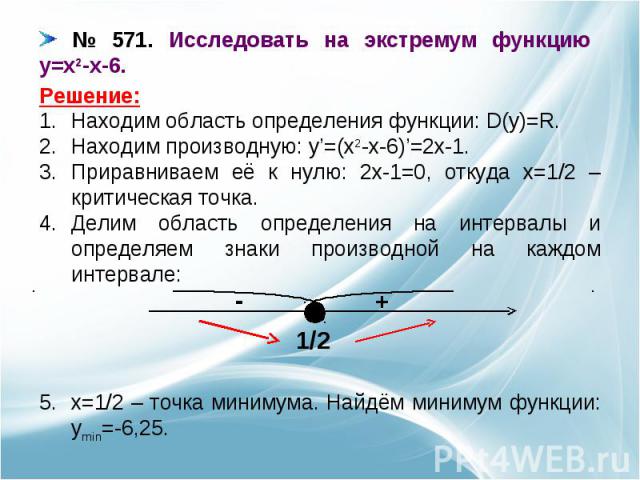
№ 571. Исследовать на экстремум функцию y=x2-x-6. Находим область определения функции: D(y)=R.Находим производную: y’=(x2-x-6)’=2x-1.Приравниваем её к нулю: 2x-1=0, откуда x=1/2 – критическая точка.Делим область определения на интервалы и определяем знаки производной на каждом интервале:x=1/2 – точка минимума. Найдём минимум функции: ymin=-6,25.

Задание на дом: Учебник Лисичкин В. Т., Соловейчик И. Л.: № 572, 573, 575, 576 – стр. 253;Выучить достаточные и необходимые условия монотонности и существования экстремумов функции.