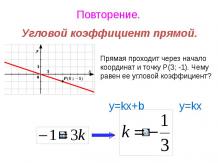
Презентация на тему: Применение производной к исследованию функций

Применение производной к исследованию функцийЧугуева Любовь Николаевна. Учитель математики МБОУ СОШ №59 п. Белозёрный.

СОДЕРЖАНИЕ.Задания на соответствие.Математическое лото.Устные задания.

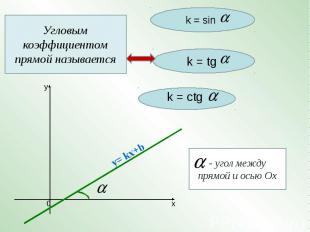
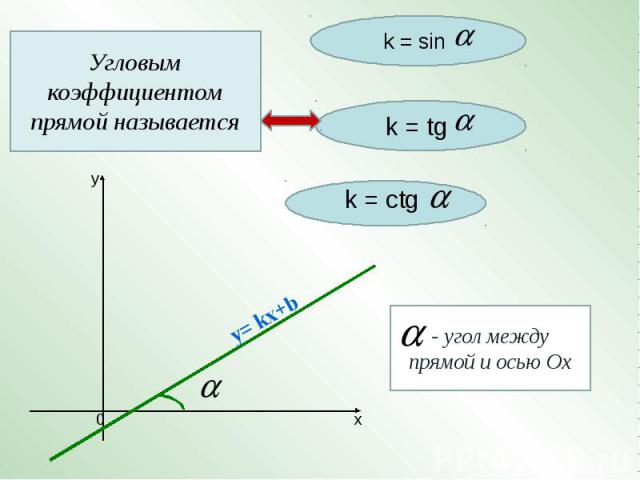
Угловым коэффициентом прямой называется

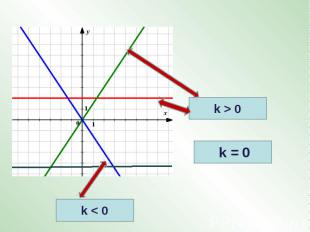
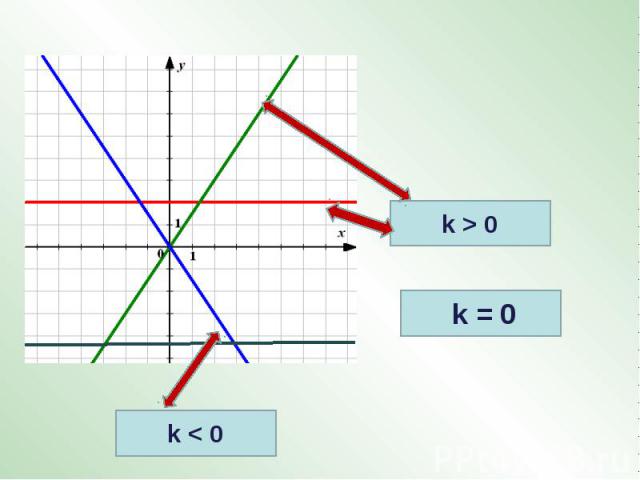
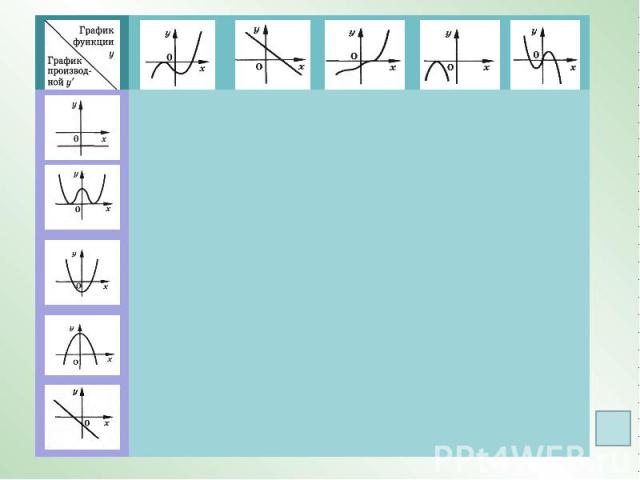
Для каждой линейной функции найдитекоэффициент k.

Геометрический смысл производной состоит в том, что значение производной функции f(х) в точке х0 равно угловому коэффициенту касательной к графику функции у = f(х) в точке(х0; f(х0)).

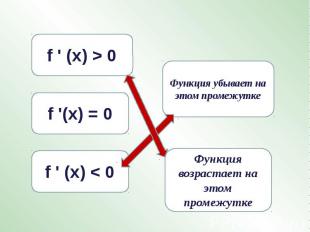
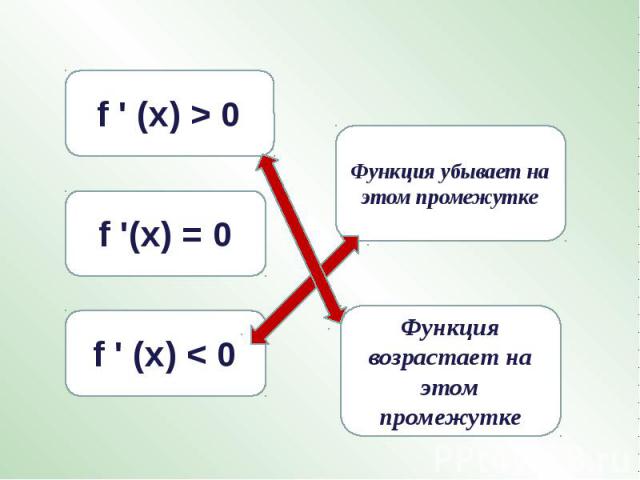
Функция убывает на этом промежуткеФункция возрастает на этом промежутке

Стационарными называют точки, в которых производная функции

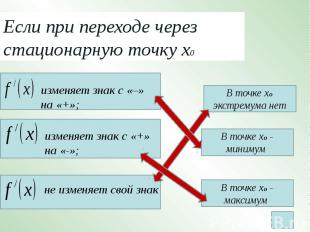
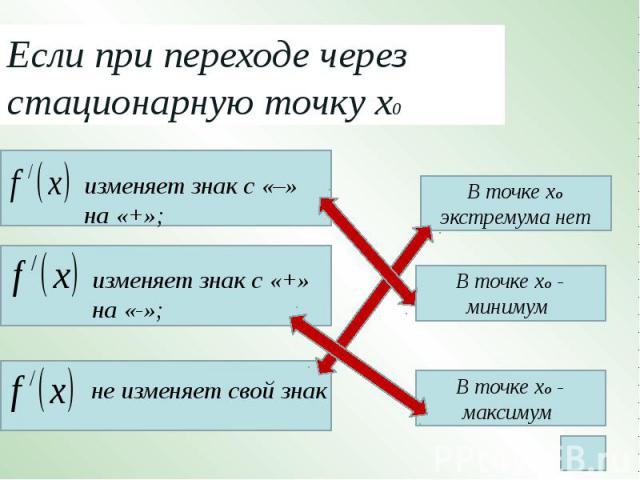
Если при переходе через стационарную точку х0 изменяет знак с «–» на «+»;изменяет знак с «+» на «-»;не изменяет свой знак

Непрерывная функция у = f(x) задана на отрезке [a; b]. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.

Непрерывная функция у = f(x) задана на отрезке [a; b]. На рисунке изображен график ее производной у = f/(x). В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.

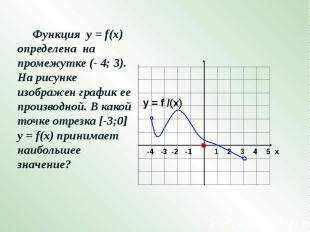
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. В какой точке отрезка [-3;0] у = f(x) принимает наибольшее значение?

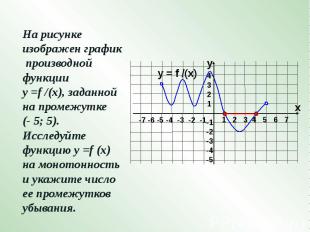
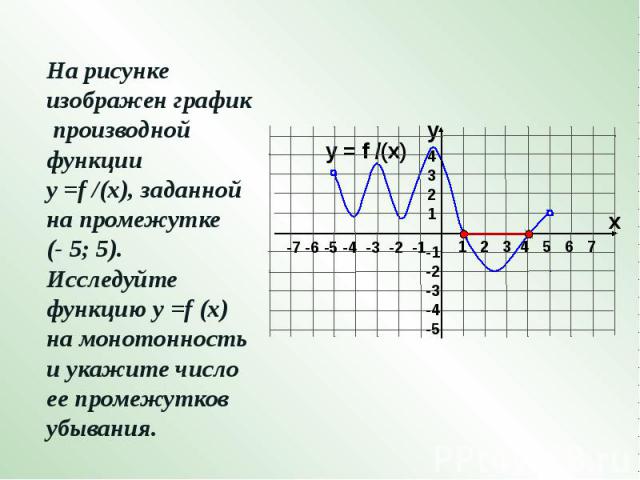
На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 5; 5). Исследуйте функцию у =f (x) на монотонность и укажите число ее промежутков убывания.

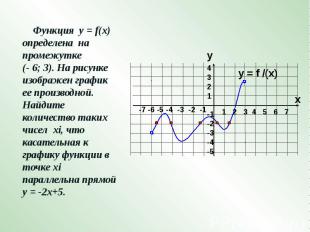
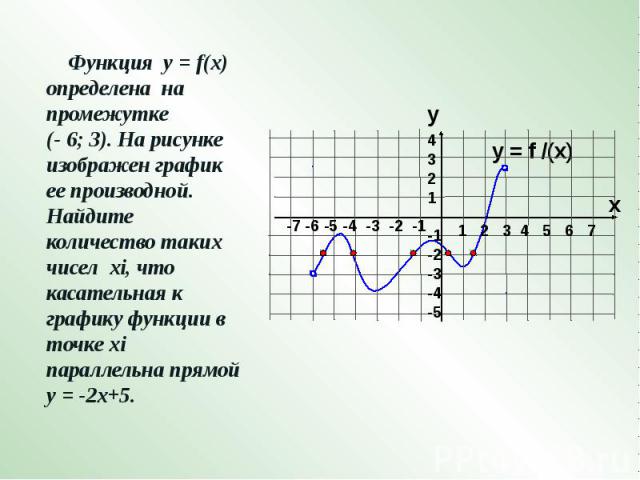
Функция у = f(x) определена на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите количество таких чисел хi, что касательная к графику функции в точке хi параллельна прямой у = -2х+5.

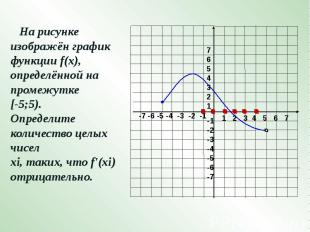
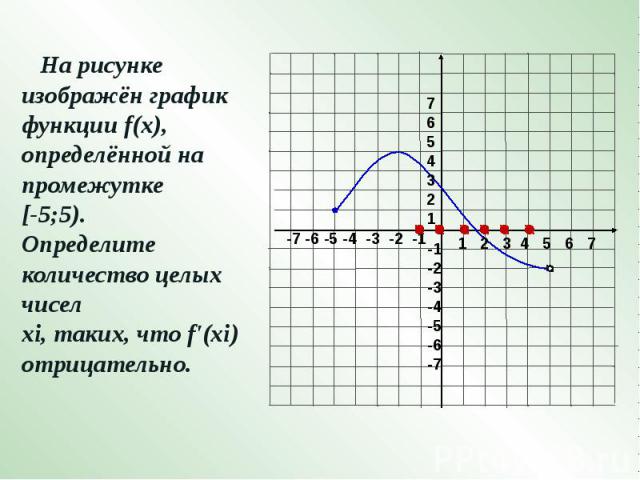
На рисунке изображён график функции f(x), определённой на промежутке [-5;5). Определите количество целых чисел хi, таких, что f'(xi) отрицательно.

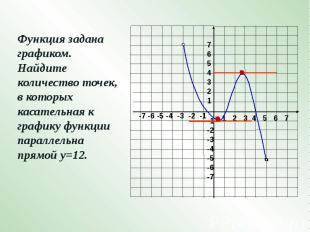
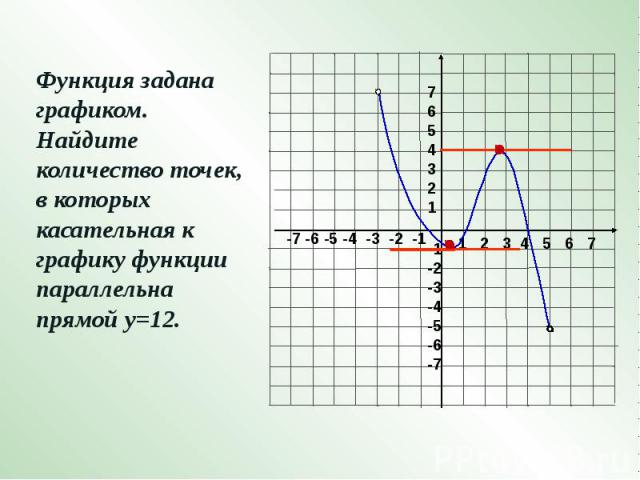
Функция задана графиком. Найдите количество точек, в которых касательная к графику функции параллельна прямой у=12.

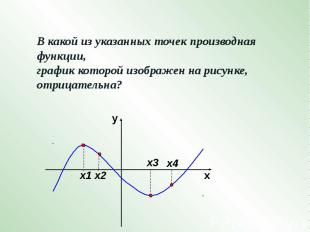
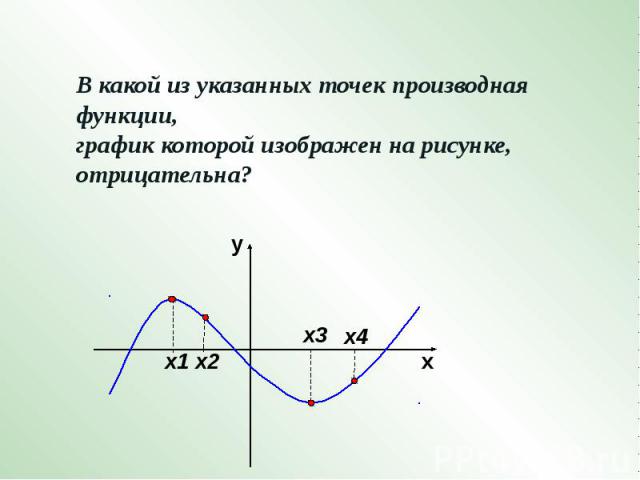
В какой из указанных точек производная функции, график которой изображен на рисунке, отрицательна?

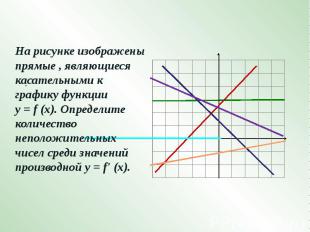
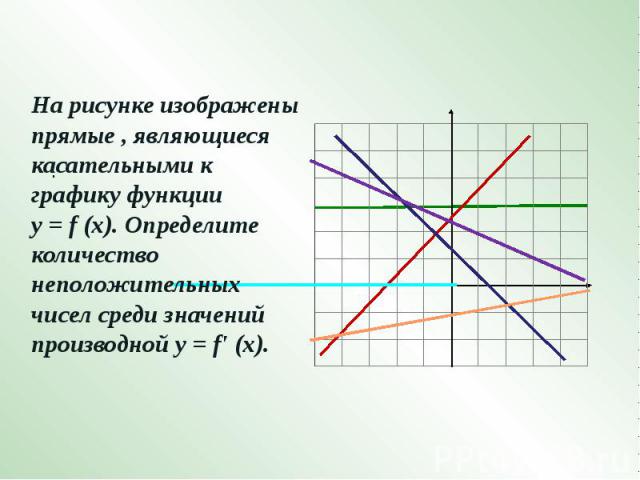
На рисунке изображены прямые , являющиеся касательными к графику функции у = f (х). Определите количество неположительных чисел среди значений производной у = f' (х).

Непрерывная функция у = f(x) задана на отрезке [a;b]. На рисунке изображен график её производной. В ответе укажите количество точек экстремума, количество точек минимума.

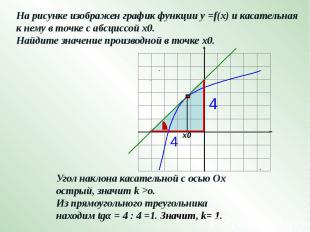
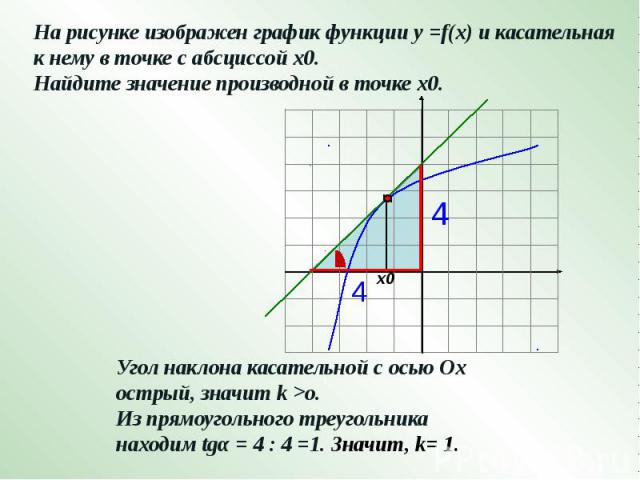
На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х0.Угол наклона касательной с осью Ох острый, значит k >o.Из прямоугольного треугольника находим tgα = 4 : 4 =1. Значит, k= 1.

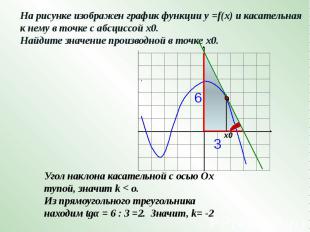
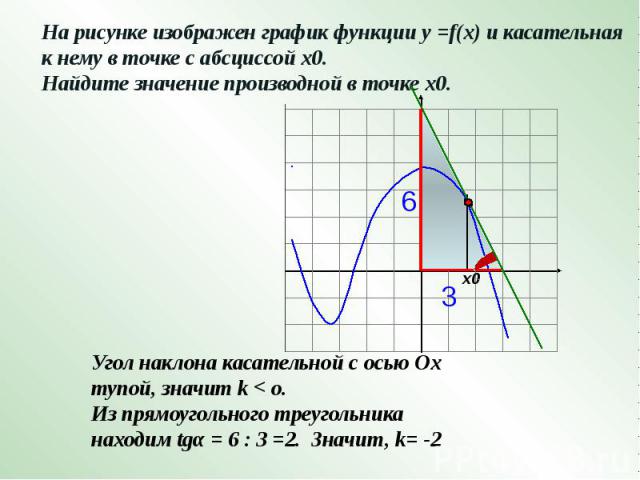
На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х0.Угол наклона касательной с осью Ох тупой, значит k < o.Из прямоугольного треугольника находим tgα = 6 : 3 =2. Значит, k= -

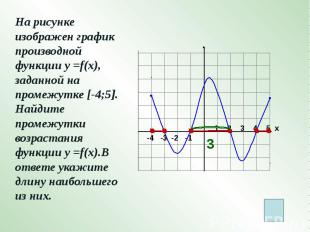
На рисунке изображен график производной функции у =f(x), заданной на промежутке [-4;5]. Найдите промежутки возрастания функции у =f(x).В ответе укажите длину наибольшего из них.

Диагностическая работа №2.