Презентация на тему: Моделирование текстовых задач при обучении математике

Моделирование текстовых задач при обучении математике Боженко Наталья ВладимировнаУчитель математикивысшей категории МОБУ СОШ №31

Одна из основных задач курса математики в школе – сформировать у учащихся умение решать текстовые задачи Подготовительный этап должен быть направлен на усвоение детьми операций над величинами и установление отношений между величинами на предметной основе. Этому будут способствовать упражнения:на оценивание количественных изменений, происходящих с величинами;на объединение двух предметных величин;на удаление из предметного множества его части;на увеличение (уменьшение) предметного множества на несколько единиц;на разностное сравнение двух предметных множеств.

Первый этап работы над задачей – это знакомство с нею. Уже в этом первичном знакомстве содержится анализ, который развивается в дальнейшем. Цель анализа при решении текстовой задачи – выделение «ведущего» отношения среди множества других, установление связей данных и искомого.На втором этапе – в роли моделей выступают не конкретные предметы, о которых идет речь в задаче, а их символические заменители (например, круги, квадраты, отрезки, точки и т.п.). В качестве моделей учитель может использовать схемы, чертежи, алгебраические выражения.

Моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей. Модель – это объект или система, исследование которой служит средством для получения знаний о другом объекте-оригинале или прототипе модели. (Л.М. Фридман, К.Н. Волков)Модель в широком смысле - это любой образ, описание, схема, чертеж, карта и т. п. какого либо процесса или явления, используемый в качестве его заменителя или представителя. Сам объект, процесс или явление называется оригиналом данной модели.

Основные этапы моделирования: 1. Постановка задачи.2. Изучение теоретических основ и сбор информации об объекте оригинала.3. Формализация.4. Выбор метода решения.5. Реализация модели.6. Анализ полученной информации.7. Проверка адекватности реальному объекту.

Как алгоритм математической деятельности метод математического моделирования содержит три этапа: * построение математической модели объекта (явления, процесса); *исследование полученной модели, т. е. решение полученной математической задачи средствами математики; *интерпретация полученного решения с точки зрения исходной ситуации.

А. Г. Мордкович пишет: "Нам нужно научиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают еще геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Графические модели также иногда называют геометрическими, а вместо термина "алгебраическая модель" используют термин "аналитическая модель". Все это — виды математических моделей"

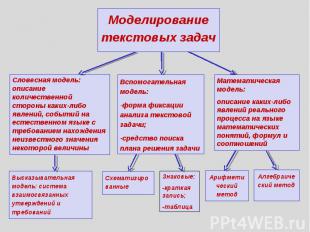
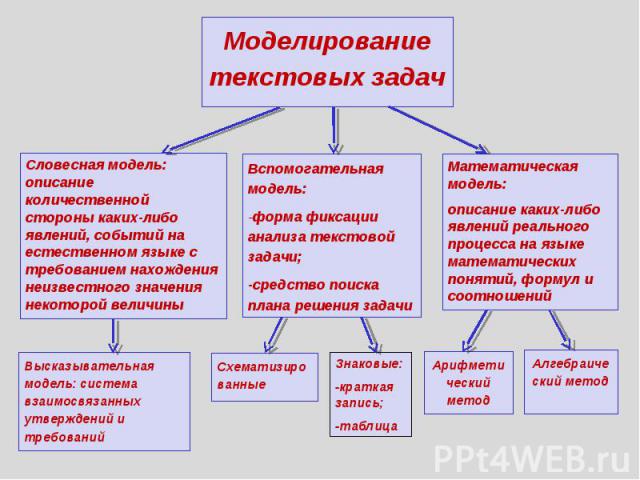
Моделирование текстовых задач Словесная модель: описание количественной стороны каких-либо явлений, событий на естественном языке с требованием нахождения неизвестного значения некоторой величины Высказывательная модель: система взаимосвязанных утверждений и требований Вспомогательная модель:-форма фиксации анализа текстовой задачи;-средство поиска плана решения задачи Схематизированные Знаковые:-краткая запись;-таблица Математическая модель: описание каких-либо явлений реального процесса на языке математических понятий, формул и соотношений Арифметический метод Алгебраический метод

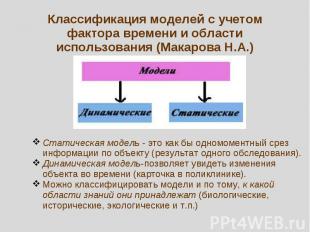
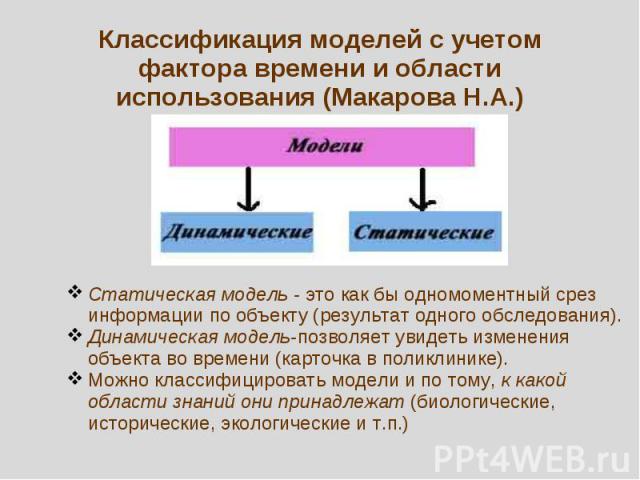
Классификация моделей с учетом фактора времени и области использования (Макарова Н.А.) Статическая модель - это как бы одномоментный срез информации по объекту (результат одного обследования).Динамическая модель-позволяет увидеть изменения объекта во времени (карточка в поликлинике).Можно классифицировать модели и по тому, к какой области знаний они принадлежат (биологические, исторические, экологические и т.п.)

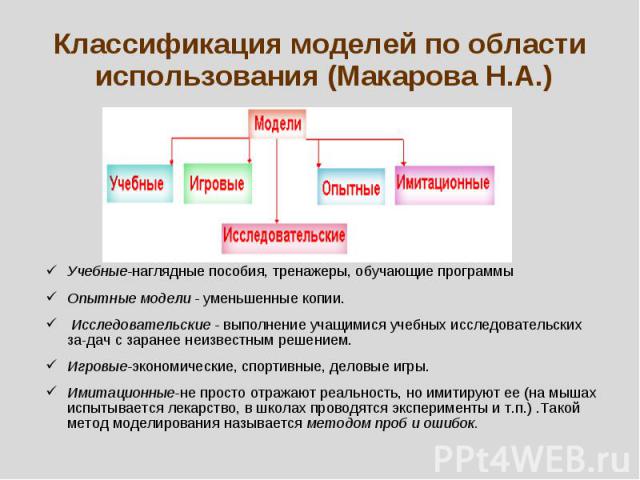
Классификация моделей по области использования (Макарова Н.А.) Учебные-наглядные пособия, тренажеры, обучающие программыОпытные модели - уменьшенные копии. Исследовательские - выполнение учащимися учебных исследовательских задач с заранее неизвестным решением.Игровые-экономические, спортивные, деловые игры.Имитационные-не просто отражают реальность, но имитируют ее (на мышах испытывается лекарство, в школах проводятся эксперименты и т.п.) .Такой метод моделирования называется методом проб и ошибок.

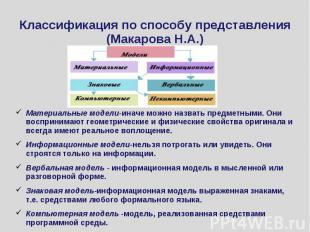
Классификация по способу представления (Макарова Н.А.) Материальные модели-иначе можно назвать предметными. Они воспринимают геометрические и физические свойства оригинала и всегда имеют реальное воплощение.Информационные модели-нельзя потрогать или увидеть. Они строятся только на информации. Вербальная модель - информационная модель в мысленной или разговорной форме.Знаковая модель-информационная модель выраженная знаками, т.е. средствами любого формального языка.Компьютерная модель -модель, реализованная средствами программной среды.

Задача Один сплав, состоящий из двух металлов, содержит их в соотношении 1:2, а другой – отношении 2:3. Сколько частей каждого сплава нужно взять, чтобы получит сплав, содержащий эти металлы в отношении 17:27?

Задача Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

Значение учебных математических задач Моделирование математических задач при обучении математики имеет большое значение. Решая математическую задачу, ученик познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи, приобретает математические знания, повышает свое математическое образование. При решении математических задач ученик обучается применять математические знания в реальной жизни, готовится к практической деятельности в будущем, к решению жизненоважных проблем. Решение математических задач приучает выделять посылки и заключения, данные и искомые, находить общее, и особенно в данных, сопоставлять и противопоставлять факты.