Презентация на тему: Показательная функция

Показательная функция Определение. Функция, заданная формулой у = ах (где а > 0, а ≠ 1, х – показатель степени), называется показательной функцией с основанием а.
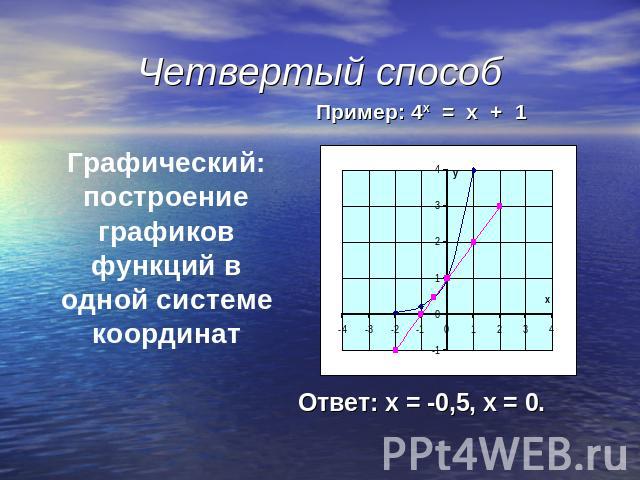
График показательной функции.

Свойства показательной функции при а>0:1.Область определения – множество действительных чисел.2.Область значений – множество положительных действительных чисел.3.Функция возрастает на всей числовой прямой. 4.При х = 0, у = 1, график проходит через точку (0; 1) при 0 < а < 1:1. Область определения – множество действительных чисел.2. Область значений – множество положительных действительных чисел. 3. Функция убывает на всей числовой прямой. 4. При х = 0, у = 1, график проходит через точку ( 0 ; 1).

Свойства функции При а >1, 0 < а <1 справедливы равенства:1. ах · ау = ах+у 2. ах : ау = ах-у3. (а ·в)х = ах · вх 4. (а/в)х = ах/ вх5. (ах)у = аху

Выполни самостоятельно! 1. Постройте график функции у = 3х 2. Сравните числа: 1. 4 ² и 4³ 2. (0,3)2 и ( 0,3)-3 3. Вычислите: 1. 21,3 · 2-0,7 · 40,7 2. (27· 64 )1/3

Показательные уравнения Показательными уравнениями называются уравнения вида аf(x) = аq(x), где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому уравнению.

Способы решения показательных уравнений

Первый способ Приведение обеих частей уравнения к одному и тому же основанию.

Второй способ Путем введения новой переменной приводят уравнение к квадратному.Пример: 4х + 2х+1 – 24 = 0Решение: Заметив , что 4х=(22 )х=( 2х)2 и 2х+1 = 2х × 21 , запишем уравнение в виде:(2х )2 + 2×2х – 24 = 0,Введем новую переменную 2х = у;Тогда уравнение примет вид:У2 + 2у – 24 = 0Д = в2 – 4 а с = 22 – 4×1×(–24) = 100> 0, находим у1 = 4, у2 = – 6.Получаем два уравнения: 2х= 4 и 2х = – 6 22 = 22 корней нет. х = 2.

Третий способ Вынесение общего множителя за скобки.
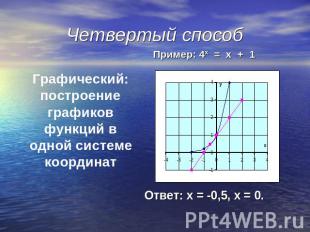
Четвертый способ Графический:построение графиков функций в одной системе координат

Выполните самостоятельно!

Показательные неравенства Показательными неравенствами называются неравенства вида аf(x) > аg(x) , где а – положительное число, отличное от нуля, и неравенства, сводящиеся к этому виду f(x) > q(x).

Свойства показательной функции Если а > 0, то показательное неравенство аf (x) > аg (x) равносильно неравенству того же смысла f(x) > q(x). Если 0 < а < 1 , то показательное неравенство аf (x) > аg (x) равносильно неравенству противоположного смысла f(x) < q(x).

Решение показательных неравенств

Выполни самостоятельно!

А. Дистервег „Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением”