Презентация на тему: Показательная функция



Степень с рациональным показателем. Степень с рациональным показателем. Показательная функция. Показательные уравнения. Показательные неравенства. Дополнительный справочный материал.

Если а>0, то: Если а>0, то: 1. 2.

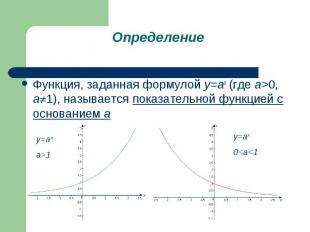
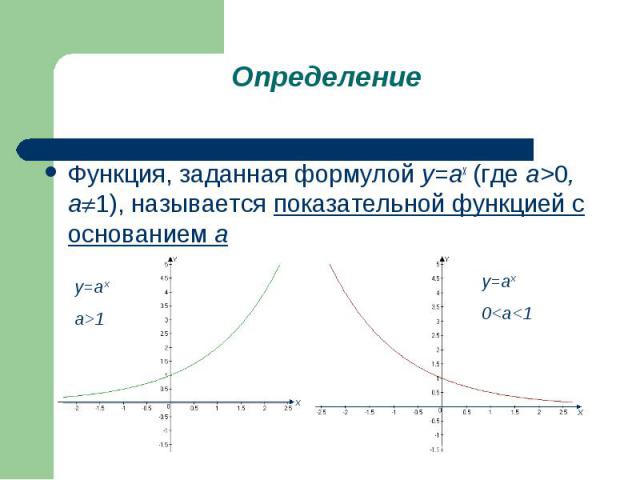
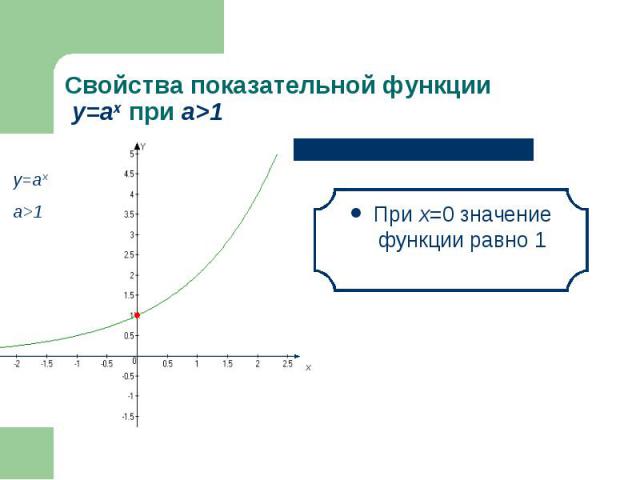
Функция, заданная формулой у=аx (где а>0, a 1), называется показательной функцией с основанием а Функция, заданная формулой у=аx (где а>0, a 1), называется показательной функцией с основанием а
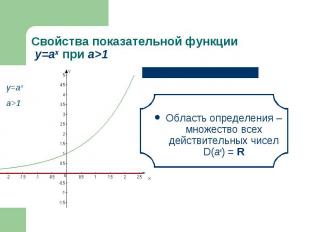
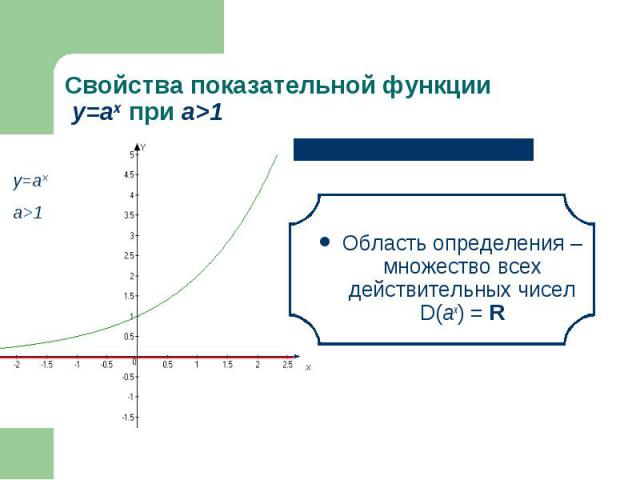
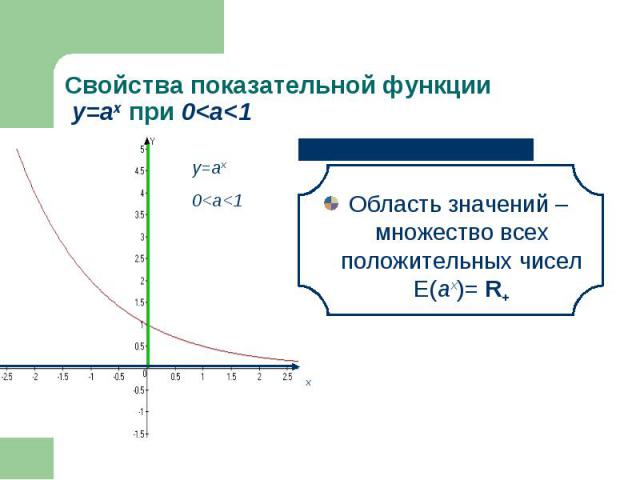
Область определения – множество всех действительных чисел D(аx) = R
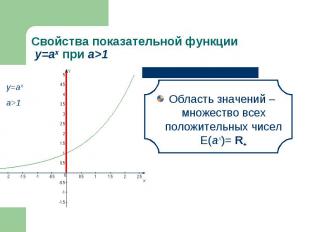
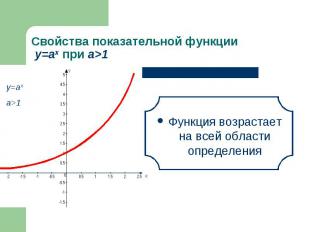
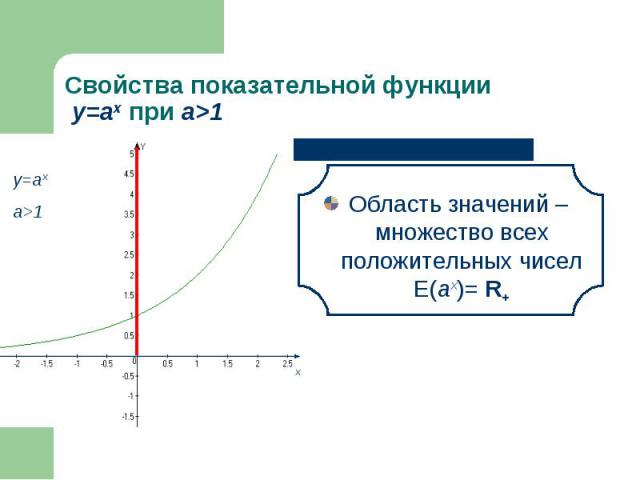
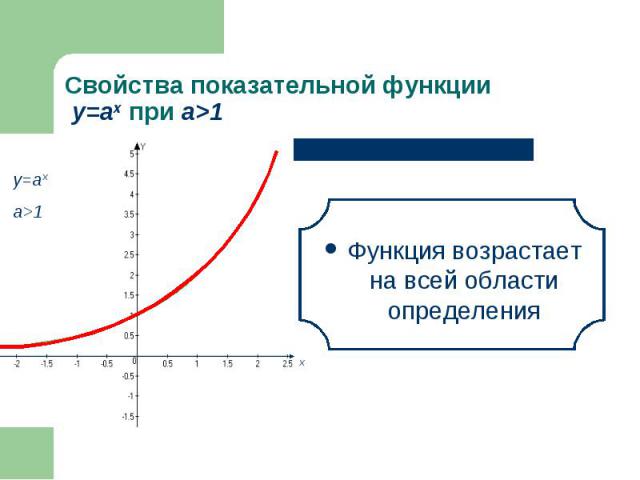
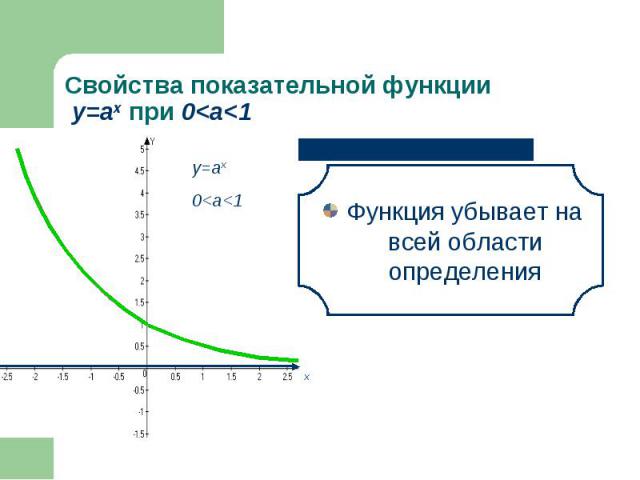
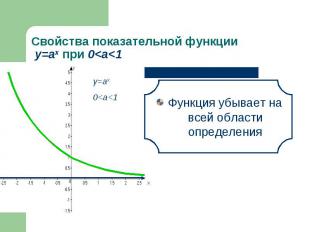
Функция возрастает на всей области определения Функция возрастает на всей области определения
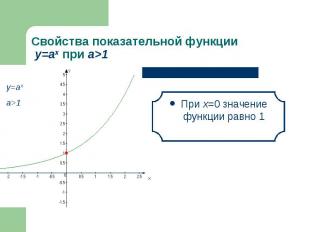
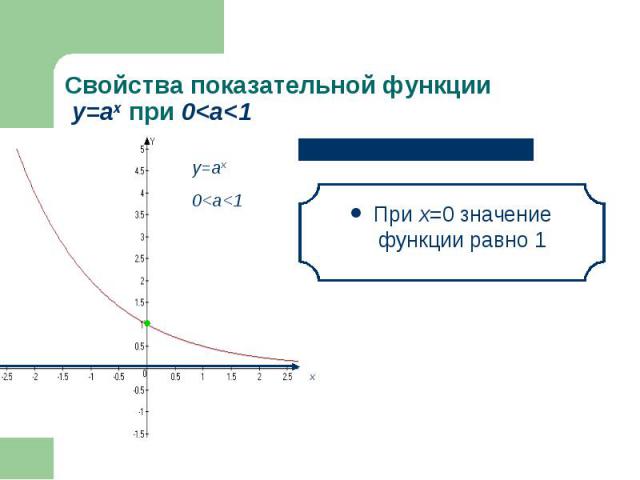
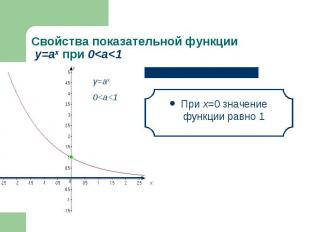
При х=0 значение функции равно 1 При х=0 значение функции равно 1
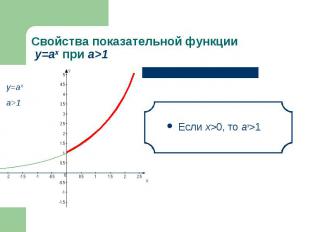
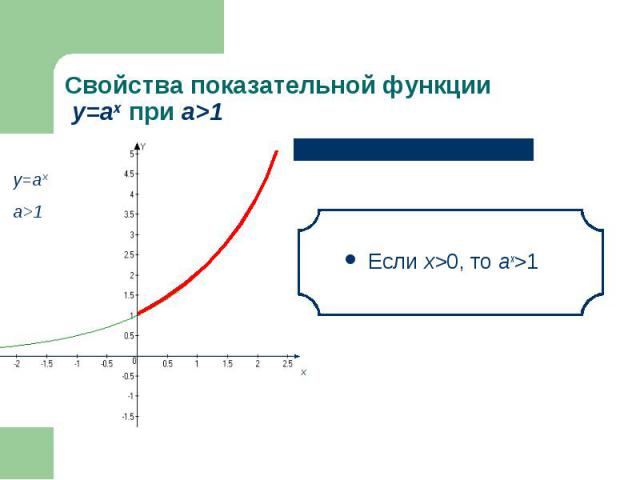
Если х>0, то аx>1 Если х>0, то аx>1
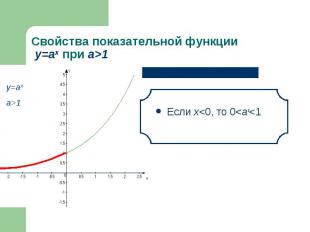
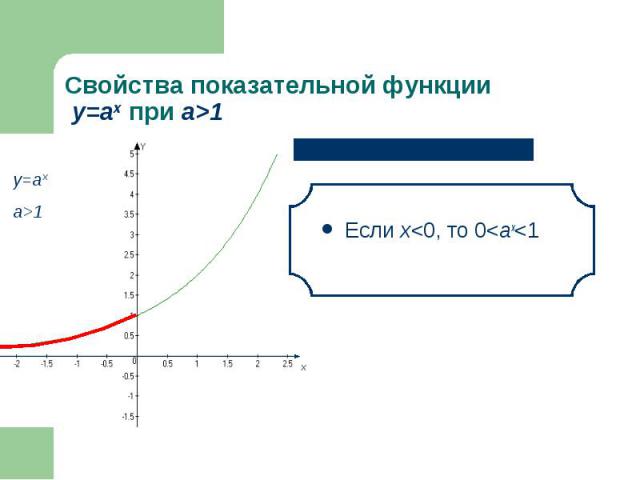
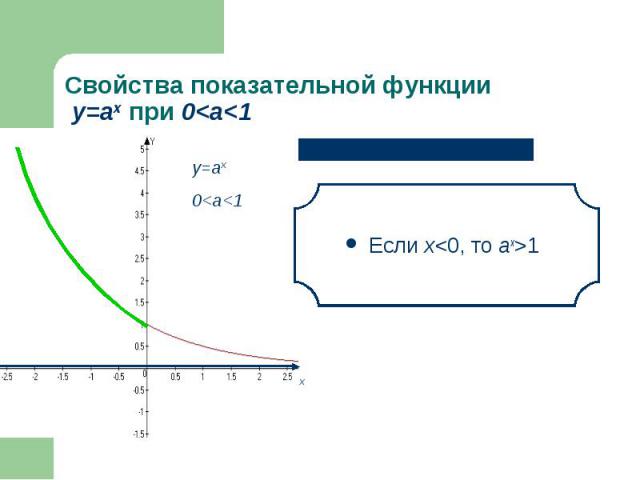
Если х<0, то 0<аx<1 Если х<0, то 0<аx<1
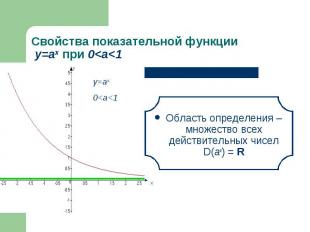
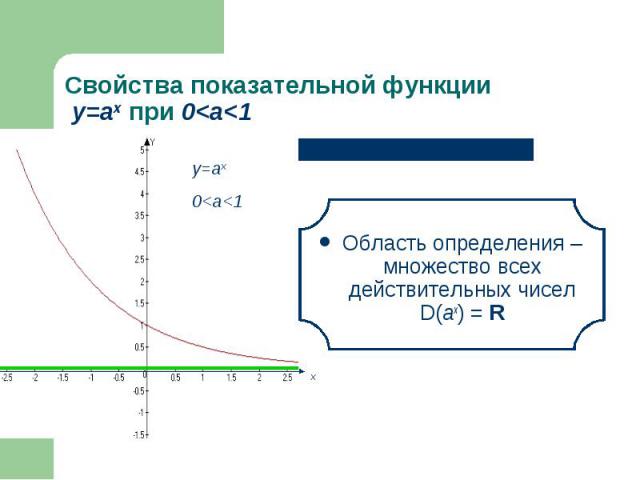
Область определения – множество всех действительных чисел D(аx) = R
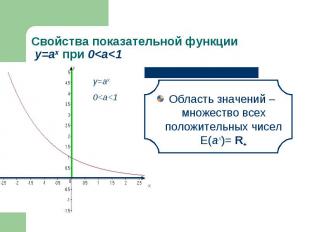
При х=0 значение функции равно 1 При х=0 значение функции равно 1
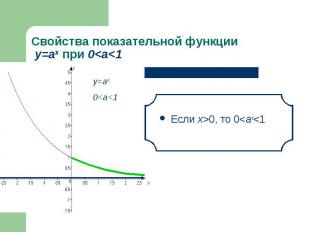
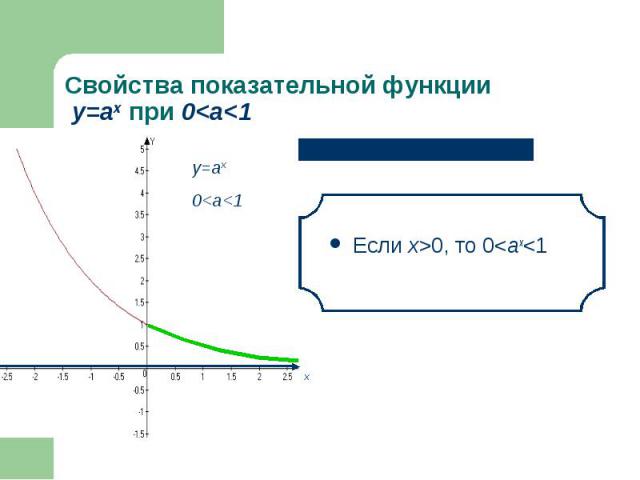
Если х>0, то 0<аx<1 Если х>0, то 0<аx<1
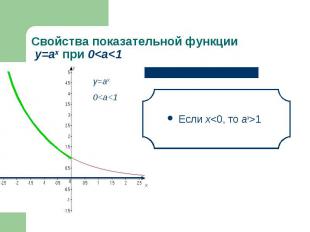
Если х<0, то аx>1 Если х<0, то аx>1




Проверь себя! Проверь себя! Да. 11. Да. Нет. 12. Да. Нет. 13. Да. Да. 14. Нет. Да. 15. Да. Да. 16. Да. Да. 17. Да. Нет. 18. Да. Нет. 19. Нет. Нет. 20. Да.

«-» 8. «-» 15. «+» «-» 8. «-» 15. «+» «-» 9. «+» 16. «-» «+» 10. «-» 17. «+» «-» 11. «+» 18. «-» «+» 12. «+» 19. «-» «-» 13. «+» 20. «-» «+» 14. «+» 21. «+»

1. 1.

Разложение левой части на множители. Разложение левой части на множители. Замена переменной. Функциональный (с помощью свойств функции). Однородные (делением обеих частей на выражение не равное нулю) Графический. Логарифмирование.

1. Опора 9 , функциональный способ 1. Опора 9 , функциональный способ 2. Опора 1 , функциональный способ 3. Опора 8 , замена переменной, функциональный способ 4. Опора 3 , функциональный способ, метод интервалов 5. Опора 6 , однородные уравнения 6. Опора 2 , замена переменной, разложение на множители 7. - замена переменной, метод интервалов 8. Опора 7 , функциональный способ 9. Опора 2 , замена переменной, функциональный способ 10. Опора 5 , 11. Опора 1 , функциональный способ 12. - , графический способ 13. Опора 5 , геометрическая прогрессия 14. Опора 4 , функциональный способ 15. - , замена переменной, метод интервалов

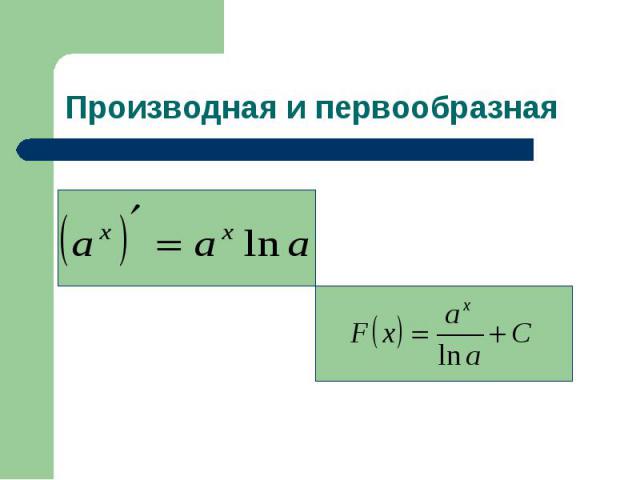
16. Используйте основное свойство дроби и исследование решений линейного уравнения. 16. Используйте основное свойство дроби и исследование решений линейного уравнения. 17. 18. Базовые знания – производная и первообразная показательной функции. 19. Записать данную функцию в виде степени с основанием 2. опереться на свойства показательной и квадратичной функций.

Вариант 1. Вариант 1.

Вариант 1 Вариант 1 Решите уравнение. В ответ запишите наименьший корень Решение. Ответ: -

Вариант 2 Вариант 2

Вариант 3 Вариант 3