Презентация на тему: Определить, чётная или нечётная функция

Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x). Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x). Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную(–x).

Например: является ли четной функция f(x) = 3x2 + 2 Например: является ли четной функция f(x) = 3x2 + 2 f(-x) = 3(-x)2 + 2 = 3x2 + 2 = f(x) – функция четная

f(x) = 2x4 - 3x2 f(x) = 2x4 - 3x2 f(x) = x3 - 2x2

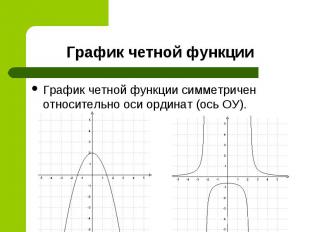
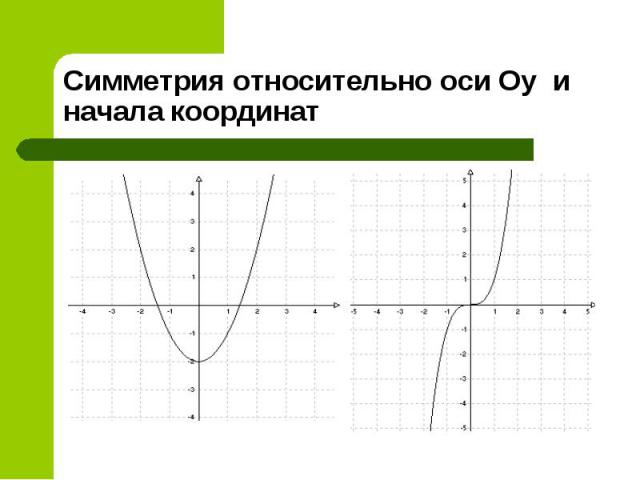
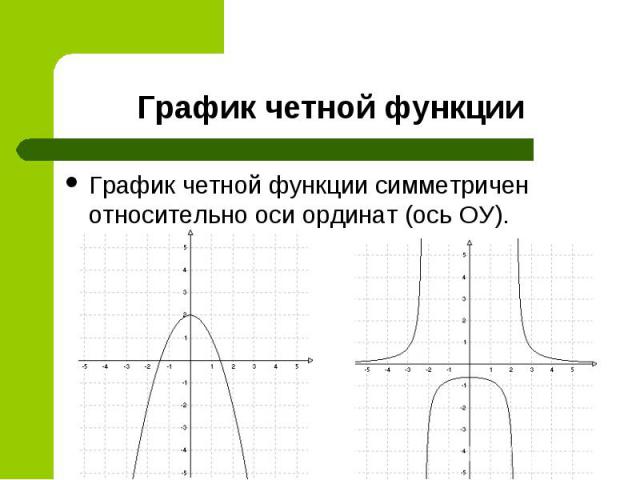
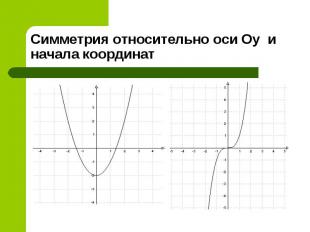
График четной функции симметричен относительно оси ординат (ось ОУ). График четной функции симметричен относительно оси ординат (ось ОУ).

Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство f(-x) = - f(x). чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную (–x) и получить первоначальную функцию с противоположными знаками.

Например: является ли нечетной функция f(x) = 3x3 + х Например: является ли нечетной функция f(x) = 3x3 + х f(-x) = 3(-x)3 + (-х) = -3x3 - х = -(3x3 + х)= = - f(x) – функция нечетная

f(x) = 2x4 + 3x f(x) = 2x4 + 3x f(x) = x3 - 2x

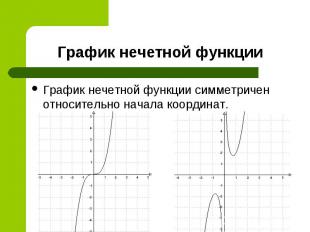
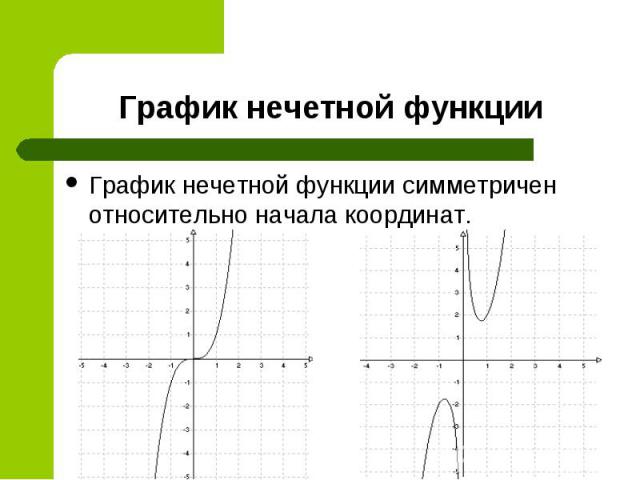
График нечетной функции симметричен относительно начала координат. График нечетной функции симметричен относительно начала координат.

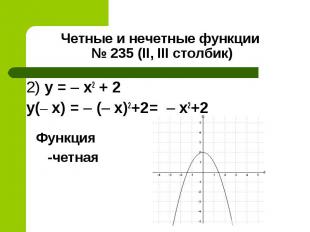
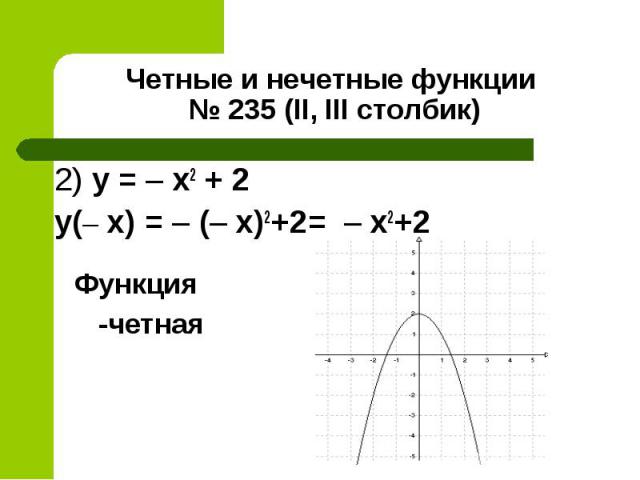
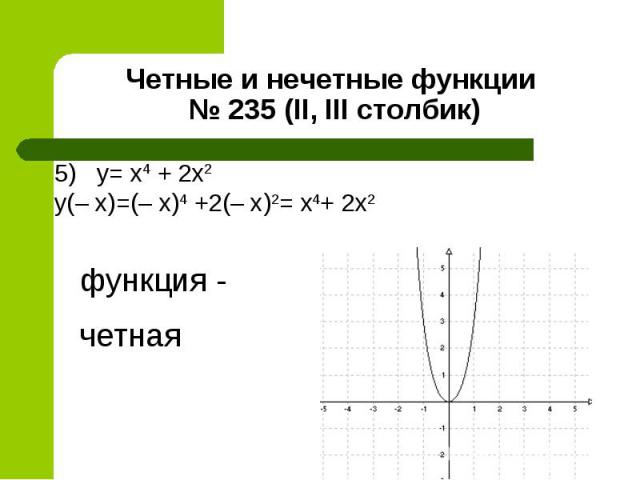
2) y = – x2 + 2 2) y = – x2 + 2 y(– x) = – (– x)2+2= – х2+2

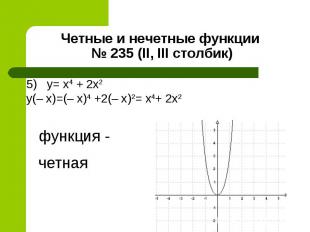
Функции могут быть как четными, нечетными, так и ни четными, ни нечетными. Функции могут быть как четными, нечетными, так и ни четными, ни нечетными.

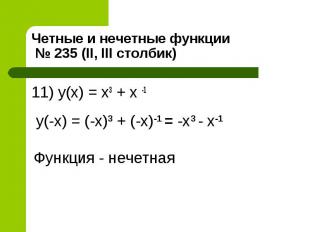
11) y(x) = x3 + x -1 11) y(x) = x3 + x -1