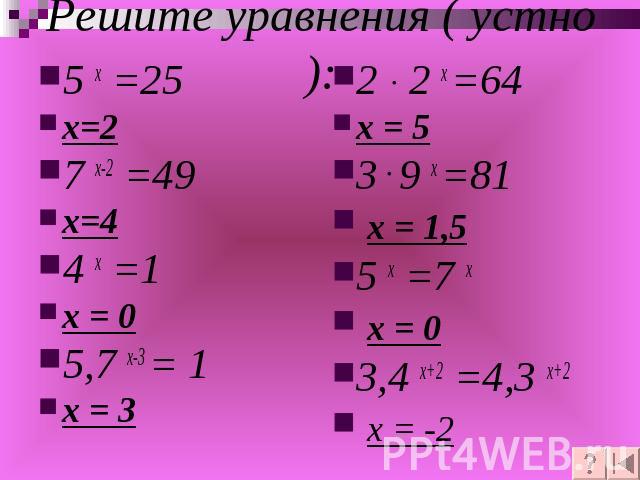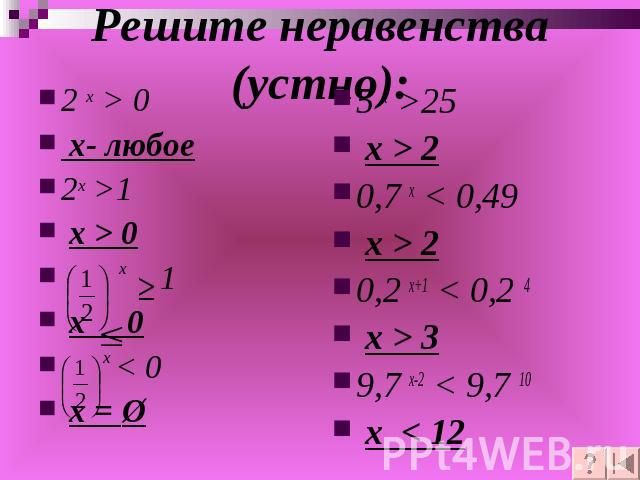Презентация на тему: Показательная функция

Показательная функция Урок обобщения и систематизации знаний

Презентация снабжена гиперссылками, при обращении к которым можно сразу перейти на выбранный слайд. Так же используются следующие управляющие кнопки: - переход к содержанию урока - переход на вопрос теории

Немного теорииРешение уравнений: устно и письменно №252(1;3) , дополнительно№264(3;4)Решение неравенств: устно и письменно №253 (3;4) , дополнительно№261(3;4)Графическое решение уравнений № 254(1) Тестирование

Показательной функцией называется функция вида у = а х , где а - заданное число, а > 0, a ≠1. монотонно возрастает монотонно убывает

Сравните

Свойства степени а х 1 ∙а х 2 = а х 1 + х 2a х 1 / а х 2 = а х 1 – х 2(а х 1) х 2 = а х 1 ∙ х 2(а ∙b) х = а х ∙b х(а / b) х = а х/ b хa х > 0a х >1, если а >1, х > 0a х 1 < а х 2, если а >1, х 1< х 2a х 1 > а х 2, если 0 < а < 1, х 1< х 2

Показательные уравнения решаются по свойству показательной функции: •если а > 0 и а ≠1, то а х1 = а х2 справедливо х1=х2

Решите уравнения ( устно): 5 х =25х=27 х-2 =49х=44 х =1х = 05,7 х-3 = 1х = 32 2 х =64х = 53 9 х =81 х = 1,55 х =7 х х = 03,4 х+2 =4,3 х+2 х = -2

№ 252(1;3) 5 2х -5 х -600 = 0Пусть 5 х =t, t > 0t 2-t- 600 = 0D=2401t 1=-24 постор.корень t 2 =25, t = 255 x =25 x=2 Ответ: 2.3 х + 9 х -1-810=03 2х-2+3х -810=032х +3х -810=0 │∙9Пусть 3х = t, t>0t2- 9t - 7290=0D = 29160t1=-90 постор.корень t2=81, t=813x=81 x=4 Ответ: 4.

Показательные неравенства решаются по следующим свойствам показательной функции: •если а > 1 , то неравенство a х 1 < а х 2 справедливо х 1< х 2 •если 0 < а < 1, то неравенство a х 1 > а х 2 справедливо х 1< х 2

Решите неравенства (устно): 2 х > 0 x- любое2x >1 x > 0 х 1 х 0 х < 0 x = Ø5 x >25 x > 20,7 x < 0,49 x > 20,2 x+1 < 0,2 4 x > 39,7 x-2 < 9,7 10 x < 12

№253(3;4) 0,7 х 2+2х < 0,7 3 y=0,7 х- убывает x 2+ 2x > 3x2+2x-3> 0, x 2+2x-3=0 x 1= -3, x 2=1(x+3) (x-1)=0Ответ: (-∞;-3) (1;+∞)

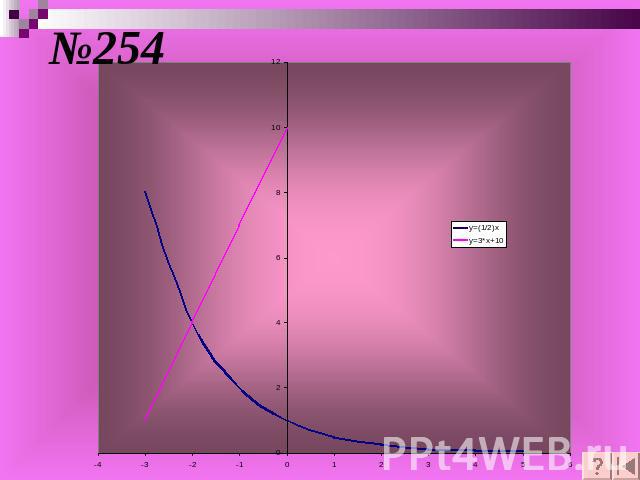
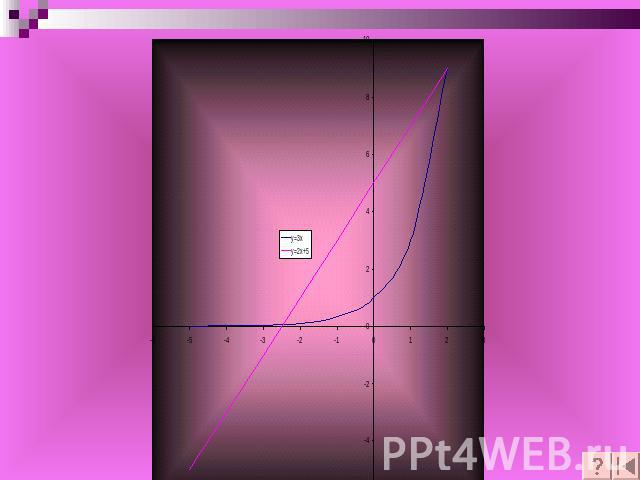
Чтобы решить графически уравнение f (x) = g (x) , надо: построить графики функций у = f (x) и у = g (x) найти абсциссу точки пересечения графиков функций рассмотреть возможность существования других точек пересечения

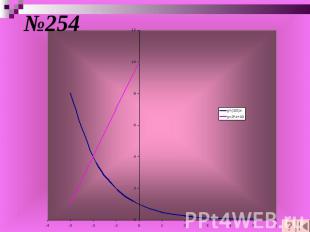
№254