Презентация на тему: Показательная функция и её свойства

Показательная функция и её свойства

Показательная функция В практике часто используются функции y=2x, y=10x, y=(0,1)x и т. д., т. е. функция вида y=ax где а - заданное число, x -переменная. Такие функции называют показательными.

Определение: Показательной функцией называется функция y=ax где а - заданное число, a>0 и a≠0.

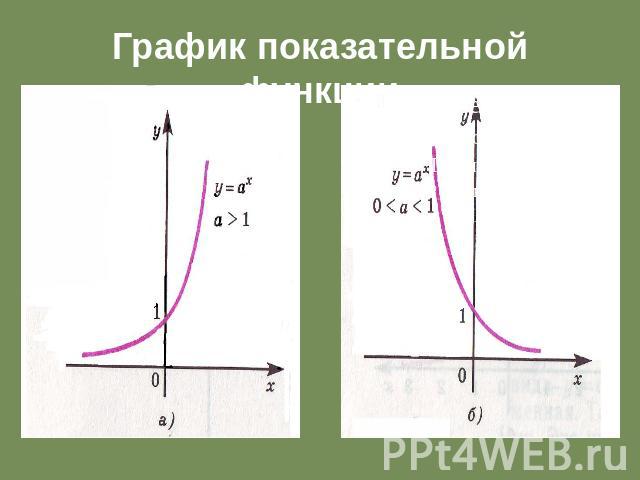
Свойства показательной функции 1) Область определения показательной функции - множество R всех действительных чисел. 2) Множество значений показательной функции - множество всех положительных чисел R+. 3) Показательная функция у=аХ является возрастающей на множестве всех действительных чисел, если а> 1, и убывающей, если 0<а<1.

График показательной функции

Показательная функция часто используется при описании различных физических процессов. Так, радиоактивный распад описывается формулой: M(t)=m0(1/2)t/T где т (t) и m0- масса радиоактивного вещества соответственно в момент времени t и в начальный момент времени t = 0, Т – период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое ). С помощью показательной функции выражается давление воздуха в зависимости от высоты подъема, ток самоиндукции в катушке после включения постоянного напряжения, и т.д.

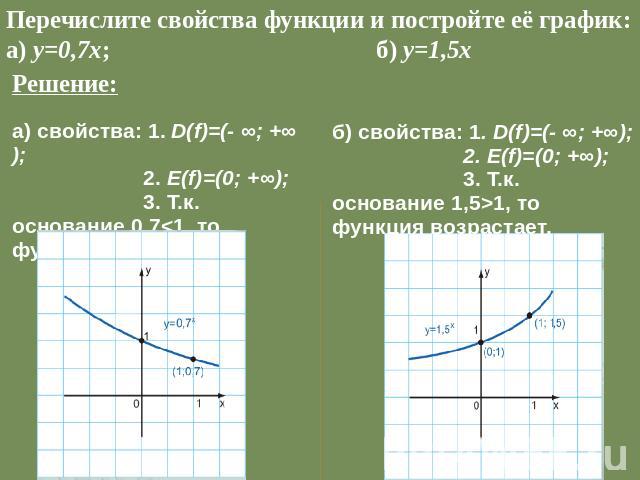
Перечислите свойства функции и постройте её график: а) у=0,7х; б) у=1,5х Решение: