Презентация на тему: Показательная функция

Показательная функция

Определение. Функцию вида называют показательной функцией

Основные свойства

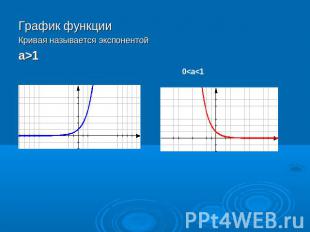
График функции Кривая называется экспонентой а>1

Геометрическая особенность графика функции Ось Ох является горизонтальной асимптотой графика функции при х→ -∞, если а >1 при х→ +∞, если 0<а<1

Показательными уравнениями называют уравнения вида а>0,а≠1, и уравнения, сводящиеся к этому виду

Основные методы решения показательных уравнений Функционально-графический Основан на использовании графический иллюстраций или каких-либо свойств функции. Метод уравнивания показателей Основан на применении теоремы: Уравнение равносильно уравнению f(x)=g(x), где а>0,а≠1. Метод введения новой переменной

Показательные неравенства Показательными неравенствами называют неравенства вида а>0,а≠1, и неравенства, сводящиеся к этому виду. Теорема: Показательное неравенство равносильно неравенству f(x)>g(x), если а >1 ; Показательное неравенство равносильно неравенству f(x) <g(x),если 0<а<1

Формулы, связанные с дифференцированием и интегрированием показательной функции: