Презентация на тему: Числовые последовательности

МОУ СОШ №5 – «Школа здоровья и развития» г. РадужныйЧисловые последовательностиАвтор: Елена Юрьевна Семёнова

Содержание Понятие числовой последовательностиПримеры числовых последовательностейСпособы задания последовательностейОграниченность числовых последовательностейВозрастание и убывание числовых последовательностейПредел числовой последовательности Гармонический рядСвойства пределовПримерыСумма бесконечной геометрической прогрессииПредел функции на бесконечностиПредел функции в точкеНепрерывность функции в точке

Понятие числовой последовательности Рассмотрим ряд натуральных чисел N: 1,  2,  3, …,  n – 1,  n, п + 1, … Функцию y = f(x), x N называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или  y1,  y2, …, yn, … или {уn}. Величина уn называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой уn = f(n), позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена.

Примеры числовых последовательностей 1,  2,  3,  4,  5, … –  ряд натуральных чисел;2,  4,  6,  8,  10, … – ряд чётных чисел;1, 4, 9, 16, 25, … – ряд квадратов натуральных чисел;5, 10, 15, 20, … – ряд натуральных чисел, кратных 5;1, 1/2, 1/3, 1/4, 1/5, ... – ряд вида 1/n, где nN;и т.д.

Способы задания последовательностей Перечислением членов последовательности (словесно).Заданием аналитической формулы.Заданием рекуррентной формулы.Примеры: Последовательность простых чисел: 2; 3; 5; 7; 11; 13; 17; 19; 23; 29; …Арифметическая прогрессия:an = a1 + (n – 1)dГеометрическая прогрессия:bn + 1 = bn ∙ q

Ограниченность числовой последовательности Последовательность {уn} называют ограниченной сверху, если все ее члены не больше некоторого числа. Последовательность {уn} ограниченна сверху, если существует число M такое, что для любого п выполняется неравенство уп ≤ МЧисло М называют верхней границей последовательности.

Ограниченность числовой последовательности Последовательность {уn} называют ограниченной снизу, если все ее члены не меньше некоторого числа. Последовательность {уn} ограниченна снизу, если существует число m такое, что для любого п выполняется неравенство уп ≥ mЧисло m называют нижней границей последовательности.Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью.

Возрастание и убывание числовой последовательности Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего:у1 < y2 < y3 < y4 < … < yn < yn+1 < … Пример: 1, 3, 5, 7, 9, 2п-1, … - возрастающая последовательность.Последовательность {уn} называют убывающей последовательностью, если каждый ее член меньше предыдущего:у1 > y2 > y3 > y4 > … > yn > yn+1 > … Возрастающие и убывающие последовательности называют монотонными

Предел числовой последовательности Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение. Число а называется пределом числовой последовательности {уn}: если для любого ε > 0 найдется такое число N = N(ε), зависящее от ε, что │un – a│< ε при n > N

Предел числовой последовательности Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a  при возрастании  n. Геометрически это значит, что для любого ε > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a – ε, a + ε). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

Рассмотрим последовательность:

Свойства пределов предел суммы равен сумме пределов:предел произведения равен произведению пределов:предел частного равен частному пределов:постоянный множитель можно вынести за знак предела:

Примеры:

Если mN, kR, то

Сумма бесконечной геометрической прогрессии

Предел функции на бесконечности Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x| > M, выполняется неравенство |f(x) - b| < ε.

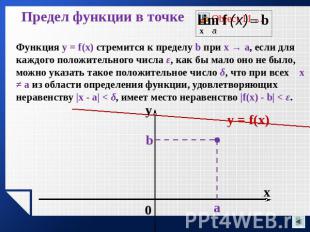
Предел функции в точке Функция y = f(x) стремится к пределу b при x → a, если для каждого положительного числа ε, как бы мало оно не было, можно указать такое положительное число δ, что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x - a| < δ, имеет место неравенство |f(x) - b| < ε.

Непрерывность функции в точке Функцию y = f(x) называют непрерывной в точкеx = a, если выполняется условие