Презентация на тему: Производная и её применение

Выполнил студент 1 курса 511 группы Таран Александр ФГОУ СПО «Приморский политехнический колледж»

Под темы: Производная Применение производной к приближенным вычислениям в геометрии и физике Применения производной к исследованию функций

Найдите десятичные приближение чисел по недостатку и по избытку с точностью до 0.1 : Примеры: А) 3/7 Б) 3/11 В) 17/9 Ответы

Найдите предел, к которому х→ 3 стремится функция, при lim ƒ (х)=2; lim g(х)=-3: A) f(x) * g(x) Б) 1/3g(x) В) f3 (x) Г) (2f(х) + (3g (x))2 Д) 2 g(х)/ƒ(x) Ответы

Найдите производные функции: Примеры: А) g(x)=2х-3 Б) g(x)=х2-2 В) g(x)=х2-3х+4 Г) g(x)=3х2-6х Ответы

Найдите производную функции: А) f(x)=(sin π /2-2x)3; Б) f(x)=(2x cos 0+x2)2; В) f(x)=(2x sin π/6+1)2; Г) f(x)=(2x2tg π/4-sin π)3 Ответы

Найдите производные функции: А) y=cos(5-3x) Б) y=sin(3-2x) В) y=ctg(2-5x) Ответы

Найдите производные функции: А) g(x)=2x3-3sin 3x Б) g(x)= √(x-2) +cos(x2-2) Ответы

Найдите производные функции: А) h(x)=tgx+tg3x/1-tgx*tg3x Б) h(x)=cos24x+sin24x В)h(x)=1-cos2x/sinx Ответы

Найдите значение производной функции y=cos x при: А) x=π/2 Б) x=-π В)x=π/6 Ответы

Сравните значения выражений: А) f’(0) и g’(π/2) Б) f’(π/4) и g’(π/3) если f(x)=tgx и g(x)=ctgx Ответы

При каких значениях x выполняется неравенство f’(x)

Определите при каких значениях переменной х верно равенство f’(x)=g’(x): Если даны функции: F(x)=2cosx G(x)=√3 x+7 Ответ

При каких значениях х верно равенство f’(x)=g’(x): Если f(x)=sin2x g(x)=2x+3 Ответ перейти на: под темы

В каких точках непрерывны функции: А) многочлен P(x)=a0xn+a1xn-1+…+an-1x+an; Б) дробно-рациональная? Ответ

Решите методом интервала неравенство: А) (x-2)(x+3)>0 Б) (x-2)(x+3)≤0 В) x+2/x-1≥0 Г) (x-1)(x+2)(x-3) (x+4)

Найдите тангенс угла наклона касательной к графику функции в точке с абсциссой x0 А)f(x)=2 sinx cosx, X0= π/2 Б)f(x)=2+tg(x+ π/6),x0= π/6 В) а(x)=3-ctgx, x0= π/2 Ответ

В какой точке касательная к графику функции y=-x2+4x-3 параллельна оси абсцисс? Ответ

Движение точки происходит по закону s(t)=t2-4t+2. в какой момент времени скорость движения равна: А) 0 Б) 6 Ответ

Найдите скорость и ускорение в указанный момент времени для точки, движущейся прямолинейно по закону: А) s(t)=2t3-3t, t=1 Б) s(t)=t2+2t+1, t=3 В) s(t)=2t2-3t+4, t=2 Ответ

Две материальные точки движутся прямолинейно по законам: s1(t)=2.5t2-6t+1? S2(t)=0.5t2+2t-3 (t-время в секундах, s-путь в метрах).в какой момент времени скорость первой точки в два раза больше скорости второй? Ответ

Известно что тело массой m=5 кг движется прямолинейно по закону s(t)=t2+2 (s-путь в метрах, t-время в секундах). Найдите кинетическую энергию тела через 2с после начала движения. Ответ перейти на: под темы

Знак производной f’(x) меняется по схеме, изображенной на рисунке. определите, на каких промежутках функция возрастает и на каких убывает. Ответ

На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной функции на промежутках: А) [-5;-2) Б) (-2;3) В) (3;5] Ответ

Опишите последовательность операций, которые нужно выполнить при отыскании промежутков возрастания (убывания) функции. Ответ

Найдите промежутки возрастания (убывания) функции: А) y=2x-3 Б) y=3-2x В) y=(x-1)2 Г) y=-4x2-4x-1 Ответ
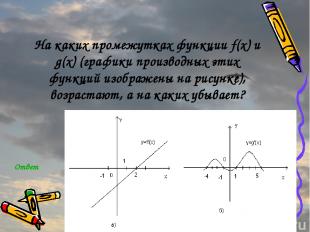
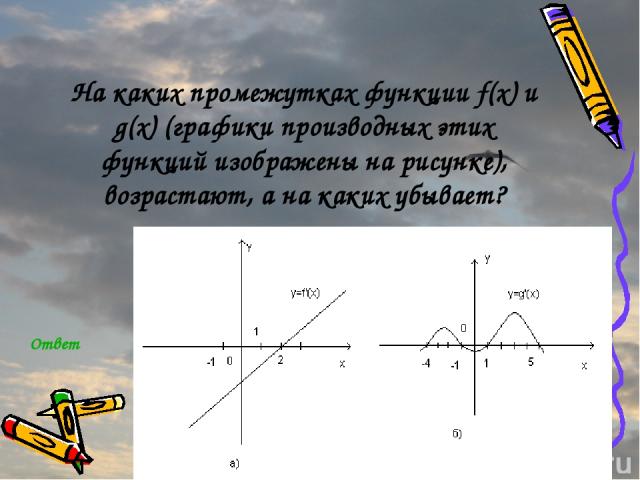
На каких промежутках функции f(x) и g(x) (графики производных этих функций изображены на рисунке), возрастают, а на каких убывает? Ответ

При каких значениях переменной x функция, графики производных которых изображены на рисунке, имеют точки максимума и минимума? Ответ
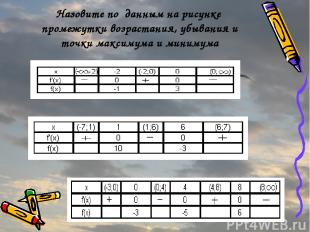
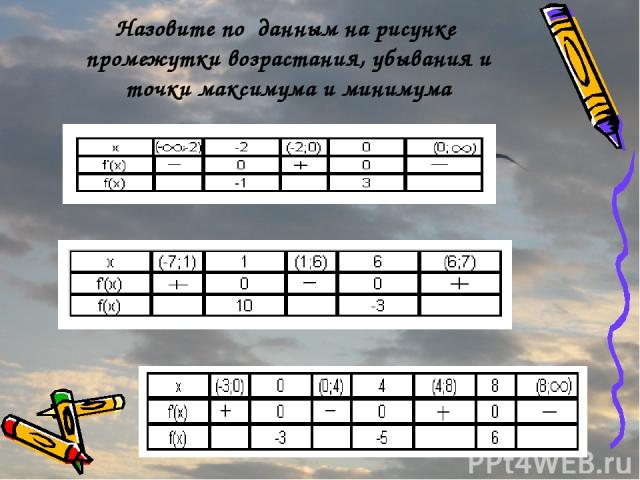
Назовите по данным на рисунке промежутки возрастания, убывания и точки максимума и минимума
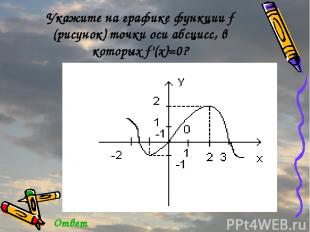
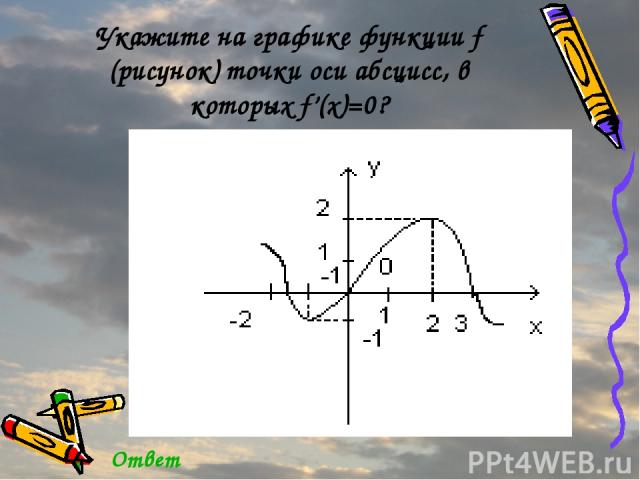
Укажите на графике функции f (рисунок) точки оси абсцисс, в которых f’(x)=0? Ответ

Исследуйте функцию на экстремум: А) f(x)=x2+2x-3 Б) f(x)=-4x2-6x-7 В) f(x)=3+4x-x2 Г) f(x)=x2+x-2 Ответ
![Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы](https://fs3.ppt4web.ru/images/132017/192756/310/img31.jpg)
Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы, равные 2 и 5, и минимум, равный 1, f(a)=-3, f(b)=0. Чему равно наименьшее и наибольшее значения функции? Ответ

Назовите амплитуду, начальную фазу и угловую частоту колебания, преобразовав правую часть к виду Acos(ωt+φ): А) x(t)=0,3 cos(2t-π/2); Б) x(t)=2 cos t В) x(t)=cos2t cos3t-sin2t sin3t Г) x(t)=cos8t cos2t+sin8t sin2t Д) x(t)=cosπ/3 cos3t-sinπ/3 sin3t Ответ

Найдите какое-нибудь отличное от нуля решение дифференциального уравнения: А) y’’=-36y Б) y’’=-1/49y В) y’’=-y Г) y’’=-6y Ответ

выход

Перейти обратно А) 0.4 и 0.5 Б) 0.2 и 0.3 В) 1.7 и 1.8

Перейти обратно а)-6; б)-1; в)8; г)25; д)-3

Перейти обратно А)2 Б)2х В)2х-3 Г)6х-6

Перейти обратно А) -6(1-2x)2 Б) 4x(2+x)(1+x) В) 2(x+1) Г) 48x5

Перейти обратно А) 3 sin(5-3x) Б) -2 cos(3-2x) В) 5/sin2(2-5x)
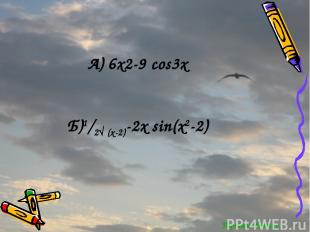
Перейти обратно А) 6x2-9 cos3x Б)1/2√ (x-2)-2x sin(x2-2)

Перейти обратно А) 4/cos24x Б) 0 В) cos x

Перейти обратно А) -1 Б) 0 В)-1/2

Перейти обратно А) f’(0)>g’(π/2) Б) f’(π/4)>g’(π/3)

Перейти обратно при любых значениях х
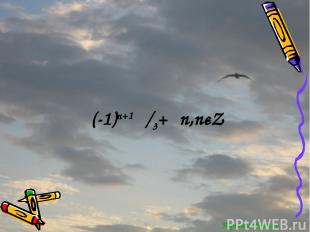
Перейти обратно (-1)n+1 π/3+πn,nєZ

Перейти обратно πn, nєZ

Перейти обратно А) многочлен не прерывен на всей числовой прямой Б) дробно-рациональная функция непрерывна во всех точках своей области определения
![Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3) Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3)](https://fs3.ppt4web.ru/images/132017/192756/310/img48.jpg)
Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3)

Перейти обратно А) -2 Б) 4 В) 1

Перейти обратно (2;0)

Перейти обратно А) t=2 Б) t=5

Перейти обратно А) 3;12 Б) 8;2 В) 5;4

Перейти обратно 2с.

Перейти обратно 40 Дж
![Перейти обратно функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция в Перейти обратно функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция в](https://fs3.ppt4web.ru/images/132017/192756/310/img55.jpg)
Перейти обратно функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция возрастает на [-6;0] и [3; ∞).

Перейти обратно А) плюс Б) минус В) плюс

Перейти обратно Найти область определения функции Найти производную заданной функции Найти значения независимой переменной, при которых значение производной положительны (отрицательны) Записать промежутки возрастания (убывания) функции
![Перейти обратно А)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], Перейти обратно А)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1],](https://fs3.ppt4web.ru/images/132017/192756/310/img58.jpg)
Перейти обратно А)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], возрастает на [1;∞) Г)возрастает на (-∞;-1/2], убывает на [-1/2;)
![Перейти обратно А) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g Перейти обратно А) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g](https://fs3.ppt4web.ru/images/132017/192756/310/img59.jpg)
Перейти обратно А) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g убывает на (-∞;-4], [1;1] и [5;∞); возрастает на [-4;-1] и [1;5]

Перейти обратно А) x=-2 –точки минимума, x=2 –точка максимума Б) x=-1, x=3 – точки минимума, x=-4, x=1 –точки максимума В) x=2 –точка максимума

Перейти обратно х=-1, х=2

Перейти обратно А) x=-1- точка минимума Б) x=-3/4 –точка максимума В) x=2 –точка максимума Г) x=-1/2 –точка минимума

Перейти обратно -3;5

Перейти обратно А)0,3;3π/2;2 Б) 2;0;1 В) 1;0;5 Г) 1;0;6; Д) 1;π/3;3

Перейти обратно А) y=3,2 cos(6t+π/4) Б) y=4cos(1/7t+π) В) y=7,5 cos(t+1) Г) y=3,7 cos(√6 t+π/7)
























![На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной функции на промежутках: А) [-5;-2) Б) (-2;3) В) (3;5] Ответ На рисунке изображен график дифференцируемой функции y=h(x). Определите знак производной функции на промежутках: А) [-5;-2) Б) (-2;3) В) (3;5] Ответ](https://fs3.ppt4web.ru/images/132017/192756/640/img23.jpg)




![Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы, равные 2 и 5, и минимум, равный 1, f(a)=-3, f(b)=0. Чему равно наименьшее и наибольшее значения функции? Ответ Известно, что на отрезке [a;b] (в области определения) функция f имеет максимумы, равные 2 и 5, и минимум, равный 1, f(a)=-3, f(b)=0. Чему равно наименьшее и наибольшее значения функции? Ответ](https://fs3.ppt4web.ru/images/132017/192756/640/img31.jpg)








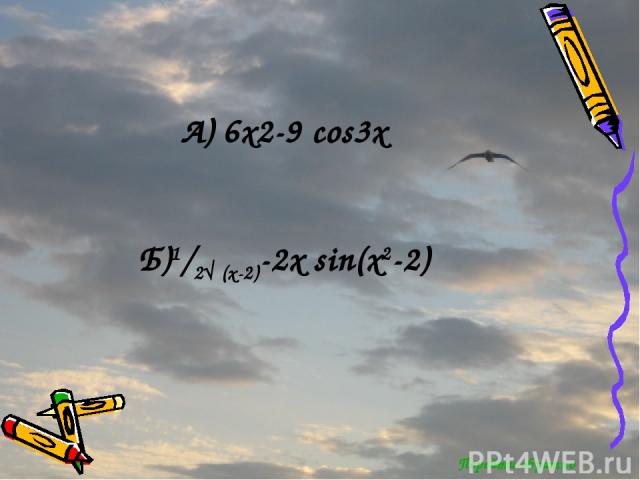




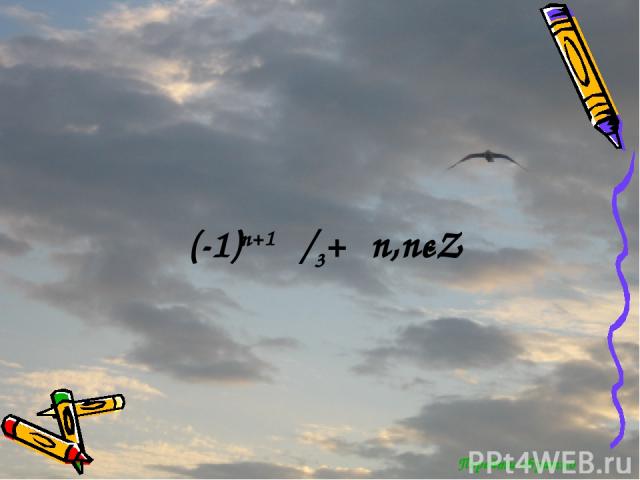


![Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3) Перейти обратно А) (-∞;-3)U(2;∞) Б) [-3;2] В) (-∞;-2]U(1;∞) Г) (-4;-2)U(1;3)](https://fs3.ppt4web.ru/images/132017/192756/640/img48.jpg)






![Перейти обратно функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция возрастает на [-6;0] и [3; ∞). Перейти обратно функция убывает на промежутках (-∞;-6], [0;1) и (1;3], функция возрастает на [-6;0] и [3; ∞).](https://fs3.ppt4web.ru/images/132017/192756/640/img55.jpg)


![Перейти обратно А)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], возрастает на [1;∞) Г)возрастает на (-∞;-1/2], убывает на [-1/2;) Перейти обратно А)возрастает на (-∞; ∞) Б)убывает на (-∞;∞) В)убывает на (-∞;1], возрастает на [1;∞) Г)возрастает на (-∞;-1/2], убывает на [-1/2;)](https://fs3.ppt4web.ru/images/132017/192756/640/img58.jpg)
![Перейти обратно А) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g убывает на (-∞;-4], [1;1] и [5;∞); возрастает на [-4;-1] и [1;5] Перейти обратно А) функция f возрастает на [2;∞), убывает на (∞;2] Б) функция g убывает на (-∞;-4], [1;1] и [5;∞); возрастает на [-4;-1] и [1;5]](https://fs3.ppt4web.ru/images/132017/192756/640/img59.jpg)