Презентация на тему: Золотое сечение или гармоническая пропорция

Золотое сечение илигармоническая пропорция

Учебный проект по математике Автор проекта: Урбаева Клара Климентьевна, зам. директора ОГОУ НПО ПУ № 59 по общеобразовательным дисциплинам, преподаватель математики и информатики

Основная идея проекта Изменить отношение учащихся к математике, показав, что фундаментальные закономерности математики являются формообразующими в архитектуре, в музыке, живописи и т.д. Показать пути взаимодействия и взаимообогащения двух сфер культуры – науки и искусства от античных времен до наших дней. Материал проекта можно использовать на занятиях факультатива, во время предметной недели, как самостоятельный проект.

Дидактические цели проекта Расширить сферу математических знаний учащихсяРазвить эстетическое восприятие математических фактовПродемонстрировать разнообразное применение математики в реальной жизниРасширить общекультурный кругозор учащихся посредством знакомства их с лучшими образцами произведений искусстваПоказать возможности применения полученных знаний в различных профессиях

Методические задачи проекта В результате участия в учебном проекте учащиеся должны уметь: Находить нужную информацию с использованием Internet-ресурсов; Работать в команде над решением единой проблемы; Планировать и реализовывать реальную проектную деятельность; Устанавливать связи между знаниями в различных учебных предметах

Что может быть общего у кроликов, Пантеона, математики, подсолнухов, искусства и сосновых шишек? Все эти вещи удивительным образом взаимосвязаны друг с другом, являясь свидетельством прекрасной, до конца не постигнутой модели в этом мире.

Иоганн Кеплер говорил что геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем.Теорему Пифагора знает каждый, а вот что такое «золотое сечение» – далеко не все. Что такое «Золотое сечение»?

Исследования научных обществОбщество математиковОбщество историков Общество биологовОбщество искусствоведов

Результаты выполнения проектной работы учащимися

Материалы преподавателяВизитная карточка проектаКритерии оценивания презентацииКритерии оценивания буклета, публикацииКроссвордТест Разработка внеклассного мероприятия

Материалы преподавателяКроссворд:Вопросы по вертикали:Арифметический знакДействие, используемое в пропорции.3. Что является корнем уравнения?4. Частное двух чисел.5. Результат решения уравнения.6. Равенство двух отношений.7. Связь двух чисел.

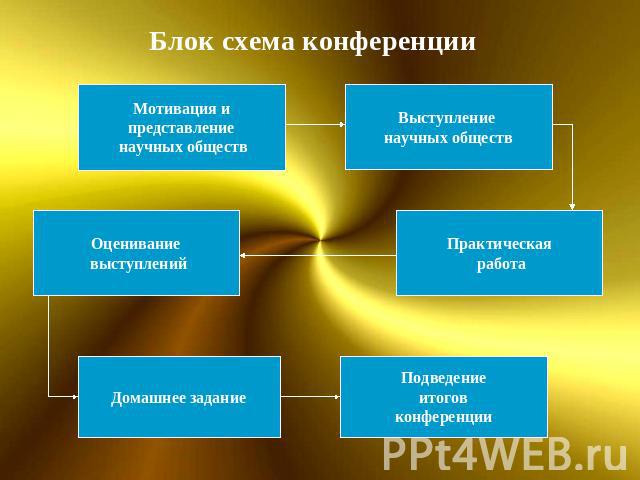
Блок схема конференции

Домашнее задание -Постройте отрезок длиной Ф, если дан квадрат со стороной 1см.-Начертите окружность радиусом 10см. впишите в нее правильный десятиугольник.-В произвольном золотом прямоугольнике изобразите логарифмическую спираль.-С помощью циркуля и линейки постройте прямоугольник с отношением сторон 1:

Что же такое «золотое сечение»? Может быть, это закон красоты? Или все-таки мистическая тайна? Научный феномен или этический принцип? «Золотое сечение» - это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна.

Ресурсы:1.Стахов А. “Коды золотой пропорции”2.Пидоу Д. “Геометрия и искусство”, М., “Мир”, 1979.3.Хембидж Д. Динамическая симметрия в архитектуре.-М,. 1936. 4.Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три взгляда на природу гармонии.-М., 1990. 5.Воробьев Н.Н. Числа Фибоначчи.-М., 1984. 6.Лосев А.Ф. Эстетика Возрожденния.-М., 1978. 7.Ковалев Ф.В. Золотое сечение в живописи/ Учебное пособие.-К., 1986. 8.Мещеряков В.Т. Гармония и гармоническое отношение.-Л., 1976. 9.Стахов А.П. Коды золотой пропорции.-М,. 1984. 10.Васютинский Н.А. Золотая пропорция. Москва, Изд-во "Молодая Гвардия", 1990 г. 11.Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. -М.: Наука, 1972. 12.Прохоров А. И. Золотая спираль. Журнал "Квант" № 9, 1984 г. 13.www. Goldenmuseum.com14.www.kyant.mccme/1973/08/zolotoe sechenie.htm