Презентация на тему: Сфера и шар 9 класс

Сфера и шар учитель математики МБОУ Одинцовской гимназии №13Владимирова Л.М.11 класс

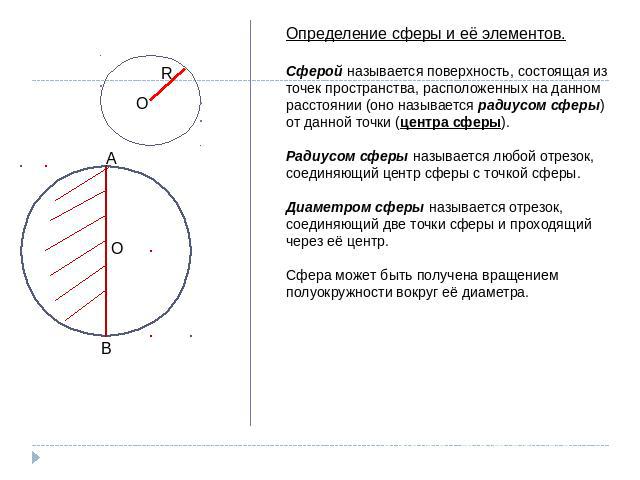
Определение сферы и её элементов.Сферой называется поверхность, состоящая из точек пространства, расположенных на данном расстоянии (оно называется радиусом сферы) от данной точки (центра сферы).Радиусом сферы называется любой отрезок, соединяющий центр сферы с точкой сферы.Диаметром сферы называется отрезок, соединяющий две точки сферы и проходящий через её центр.Сфера может быть получена вращением полуокружности вокруг её диаметра.

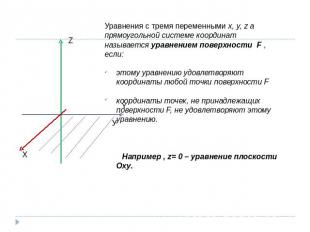
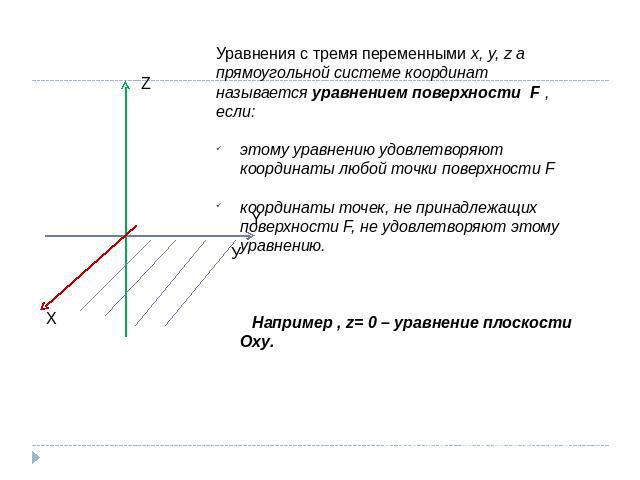
Уравнения с тремя переменными x, y, z а прямоугольной системе координат называется уравнением поверхности F , если: этому уравнению удовлетворяют координаты любой точки поверхности Fкоординаты точек, не принадлежащих поверхности F, не удовлетворяют этому уравнению. Например , z= 0 – уравнение плоскости Оху.

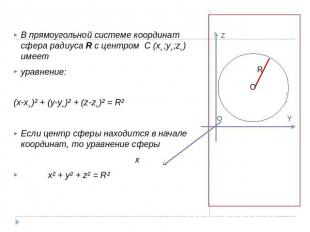
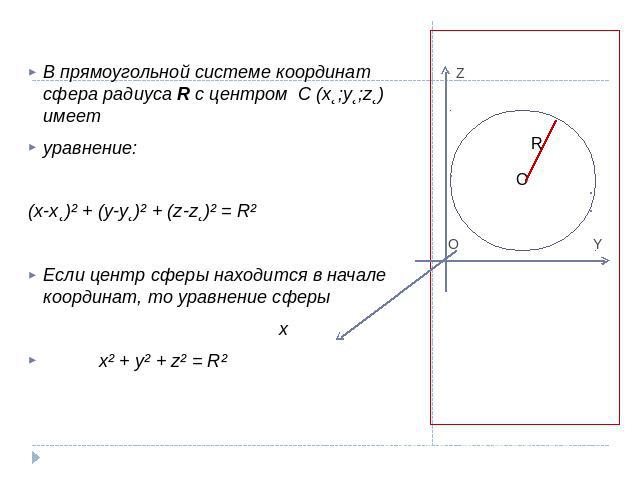
Z O YВ прямоугольной системе координат сфера радиуса R с центром C (x˛;y˛;z˛) имеет уравнение:(x-x˛)² + (y-y˛)² + (z-z˛)² = R² Если центр сферы находится в начале координат, то уравнение сферы x x² + y² + z² = R²

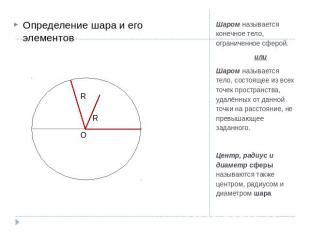
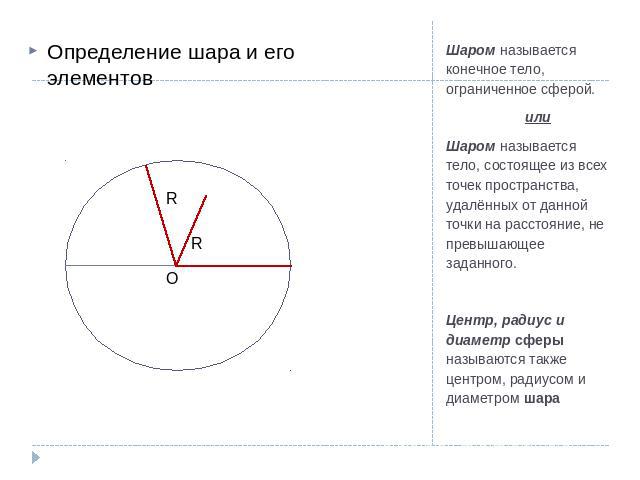
Определение шара и его элементовШаром называется конечное тело, ограниченное сферой. илиШаром называется тело, состоящее из всех точек пространства, удалённых от данной точки на расстояние, не превышающее заданного.Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара

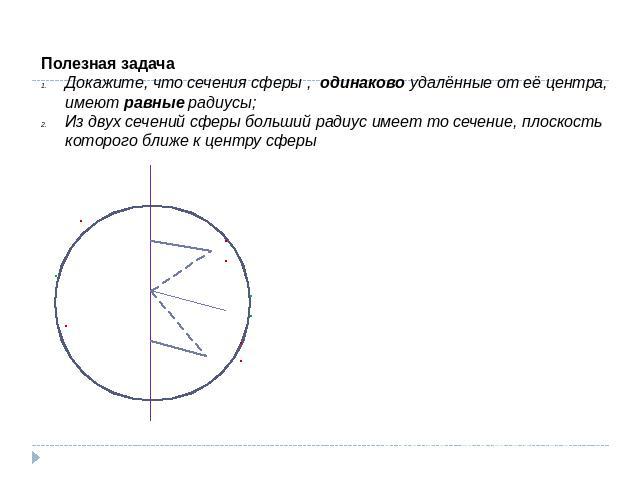
Полезная задачаДокажите, что сечения сферы , одинаково удалённые от её центра, имеют равные радиусы;Из двух сечений сферы больший радиус имеет то сечение, плоскость которого ближе к центру сферы

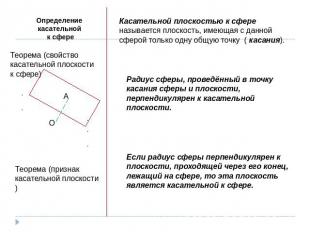
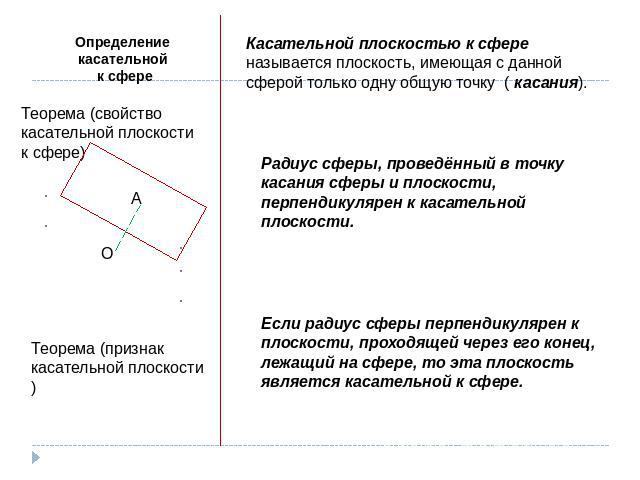
Определение касательной к сфереТеорема (свойство касательной плоскости к сфере)Теорема (признак касательной плоскости)Касательной плоскостью к сфере называется плоскость, имеющая с данной сферой только одну общую точку ( касанияРадиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

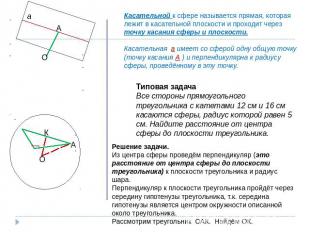
Касательной к сфере называется прямая, которая лежит в касательной плоскости и проходит через точку касания сферы и плоскости.Касательная а имеет со сферой одну общую точку (точку касания А ) и перпендикулярна к радиусу сферы, проведённому в эту точку.Типовая задачаВсе стороны прямоугольного треугольника с катетами 12 см и 16 см касаются сферы, радиус которой равен 5 см. Найдите расстояние от центра сферы до плоскости треугольника.Решение задачи.Из центра сферы проведём перпендикуляр (это расстояние от центра сферы до плоскости треугольника) к плоскости треугольника и радиус шара.Перпендикуляр к плоскости треугольника пройдёт через середину гипотенузы треугольника, т.к. середина гипотенузы является центром окружности описанной около треугольника.Рассмотрим треугольник ОАК. Найдём ОК.

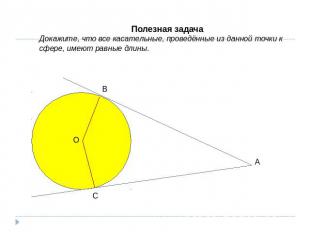
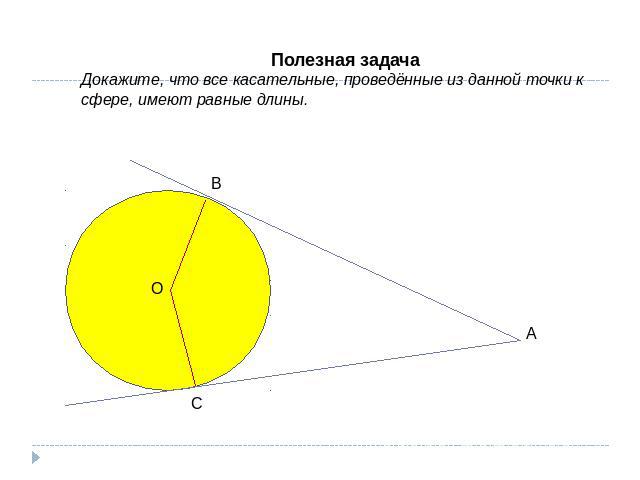
Полезная задачаДокажите, что все касательные, проведённые из данной точки к сфере, имеют равные длины.

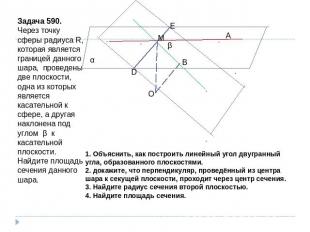
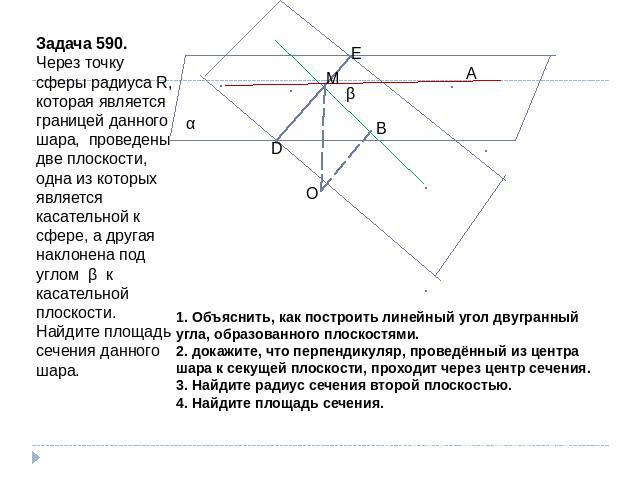
Задача 590.Через точку сферы радиуса R, которая является границей данного шара, проведены две плоскости, одна из которых является касательной к сфере, а другая наклонена под углом β к касательной плоскости. Найдите площадь сечения данного шара. 1. Объяснить, как построить линейный угол двугранный угла, образованного плоскостями.2. докажите, что перпендикуляр, проведённый из центра шара к секущей плоскости, проходит через центр сечения.3. Найдите радиус сечения второй плоскостью.4. Найдите площадь сечения.

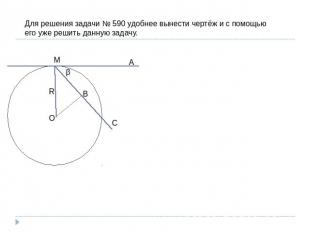
Для решения задачи № 590 удобнее вынести чертёж и с помощью его уже решить данную задачу.

Для создания презентации были использованы: учебник по геометрии автор – Атаносян Л.С.«Изучение геометрии в 10-11 классах» (методические рекомендации к учебнику) авторы Л.С. Атанасян и др.