Презентация на тему: Сфера и шар

Сфера и шар Выполнила: Скурлатова Г.Н., МОУ СОШ № 62

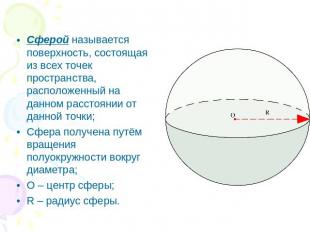
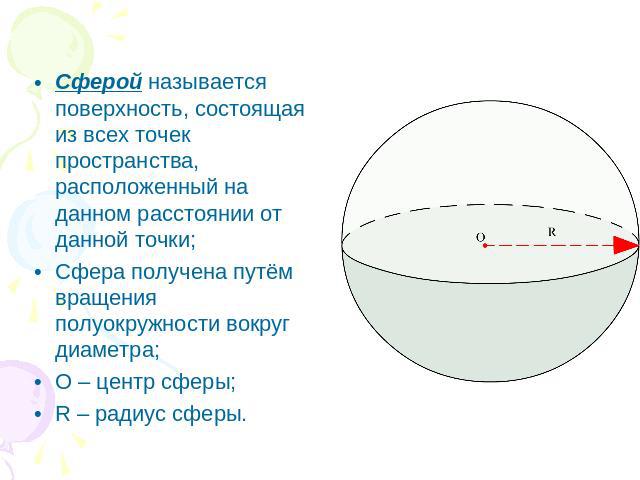
Сферой называется поверхность, состоящая из всех точек пространства, расположенный на данном расстоянии от данной точки;Сфера получена путём вращения полуокружности вокруг диаметра;О – центр сферы;R – радиус сферы.

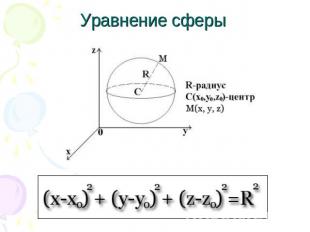
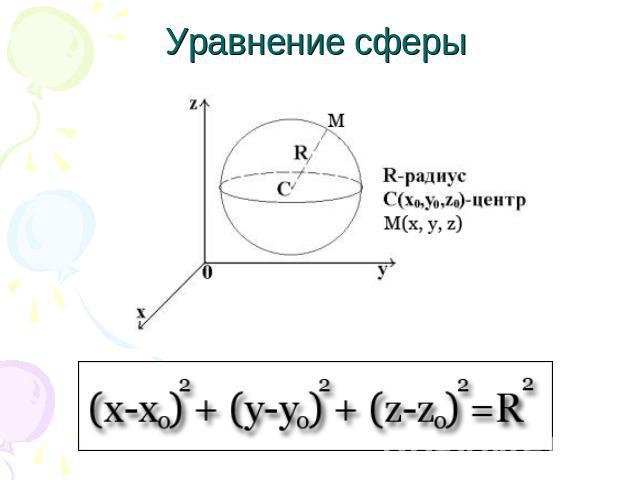
Уравнение сферы

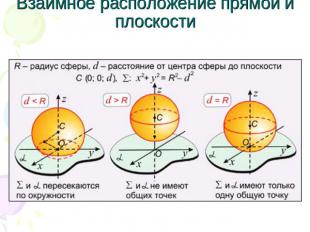
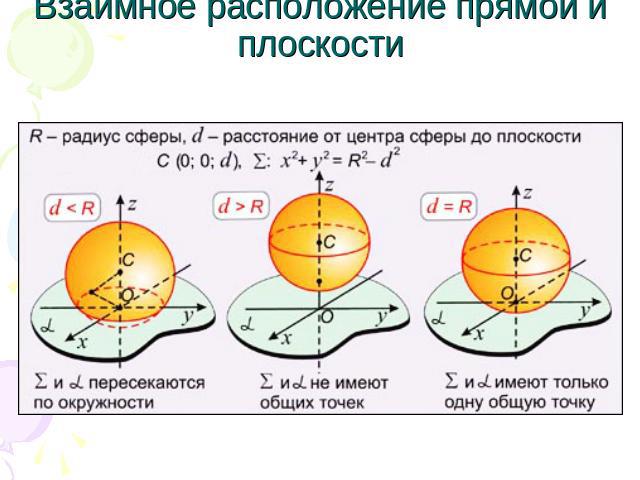
Взаимное расположение прямой и плоскости

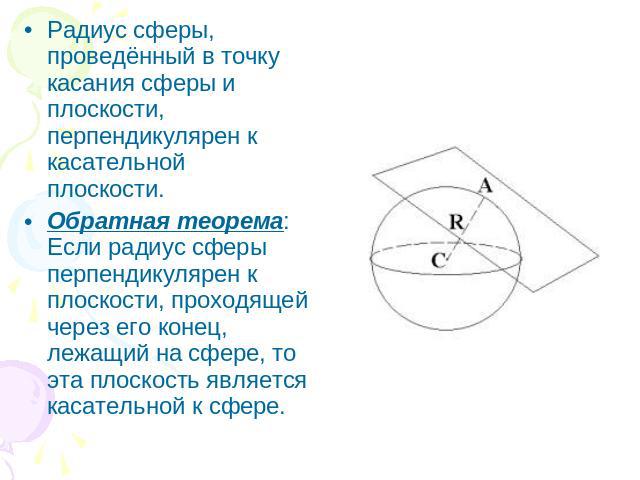
Касательная плоскость к сфере Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.Касательная плоскость к сфере обладает свойством, аналогичным свойству касательной к окружности. Оно выражено в следующей теореме ---------->

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.Обратная теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Площадь сферы В отличие от боковой поверхности конуса или цилиндра, сферу невозможно развернуть на плоскость.Для определения площади сферы используется понятие описанного многогранника: многогранник называется описанным около сферы (шара), если сфера касается всех его граней.