Презентация на тему: Музей истории четырёхугольников

Зал №1 ЧетырёхугольникиЧетырёхугольник — это геометрическая фигура, состоящая из четырёх точек, не лежащих на одной прямой, и четырёх отрезков, попарно соединяющих эти точки.

Зал №1 ЧетырёхугольникиПриглашаем в путешествие!

Зал №1 Четырёхугольники Если никакие стороны четырёхугольника не параллельны, то середина отрезка, соединяющего точки пересечения противоположных сторон, лежит на прямой, соединяющей середины диагоналей. Эта прямая называется прямой Гаусса.

Зал №1 ЧетырёхугольникиИоганн Карл Фридрих Гаусс (нем. Johann Carl Friedrich Gauß) 1777,Брауншвейг — 1855, Гёттинген. Немецкий математик, астроном и физик, величайший математик всех времён, «король математики».

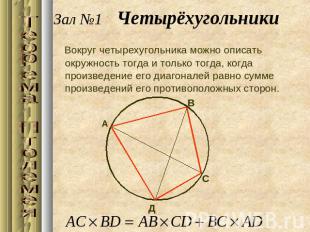
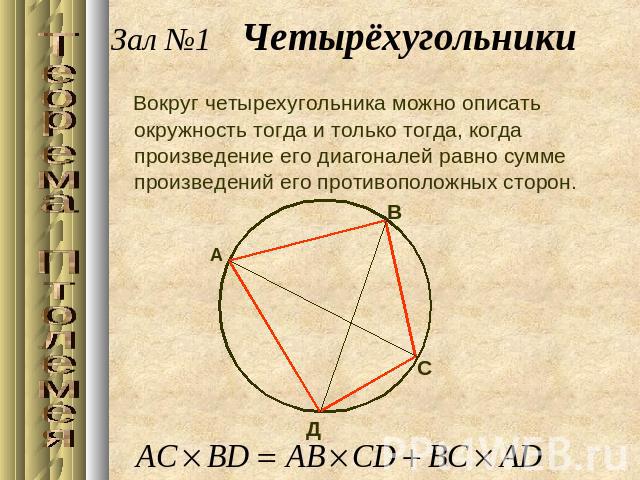
Зал №1 ЧетырёхугольникиВокруг четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.

Зал №1 ЧетырёхугольникиКлавдий Птолемей, живший в конце первого — начале второго века н.э. Древнегреческий ученый - астроном, математик, астролог, географ, оптик и теоретик музыки. . Основной труд Птолемея — “Альмагест”, в котором он изложил сведения по астрономии.

Зал №1 ЧетырёхугольникиЕсли вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке M, то прямая, проходящая через точку M и перпендикулярная одной из его сторон, делит противоположную ей сторону пополам. Формула Брахмагупты

Зал №1 Четырёхугольники00 0598 - 00 0660индийский математик и астроном Брахмагупта Основные труды: «Брахма-спхута-сиддханта» «Кхандакхадьяка»

Зал №2 Параллелограмм(др.греч. παραλληλόγραμμον от παράλληλος — параллельный иγραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Зал №2 ПараллелограммВатиканский манускрипт т.1, 38v — 39r. Euclid I prop. 47В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороныравны и противоположные углы равны, а диагональ разделяет его пополам.

Зал №2 ПараллелограммЕвклид или Эвклид (др.-греч. Εὐκλείδης, ок. 300 г. до н. э.) Древнегреческий математик. Мировую известность приобрёл благодаря сочинению по основам математики «Начала» (Στοιχεῖα букв. элементы).

Зал №2 ПараллелограммЧетырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

Зал №2 ПараллелограммПьер Вариньон (фр. Pierre Varignon, Кан, 1654 —1722, Париж) Французский математик , член Парижской Академии наук, профессор математики коллежа Мазарини профессор Коллеж де Франс. Основной вклад Вариньон совершил в статику и механику.

Зал №3 Трапецияот др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») —четырёхугольник, у которого только одна пара противолежащих сторон параллельна. «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония (1в.)

Зал №2 Трапецияродился в Апамее в Сирии в 135 г., умер в Риме в 50 г. до Р. Хр. Математик и астроном. Жил долго в Родосе. Был учителем Цицерона. Известен второй попыткой определить размеры земного шара.

Зал №2 ТрапецияСредняя линия трапеции равна полусумме ее оснований (в трудах Герона Александрийского)

Зал №3 ТрапецияГерон Александрийский (Heron, I в. н. э.) Греческий механик и математик. Занимался геометрией, механикой, гидростатикой, оптикой; изобрел прототип паровой машины и точные нивелировочные инструменты.

Зал №4 РомбТермин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Зал №4 Ромб «Собрание» (συναγωγή). Автор Папп Александрийский(др.-греч. Πάππος ὁ Ἀλεξανδρεύς) — древнегреческий математик второй половины III века.Изложено содержание ряда трудов более древних авторов,добавлены собственные теоремы Паппа. Портрет учёного не найден

Зал №4 Ромб Мозаика Пенроуза, плитки Пенроуза -непериодическое разбиение плоскости, апериодические регулярные структуры, замощение плоскости ромбами двух типов — с углами 72° и 108° и 36° и 144

Зал №5 Прямоугольник Прямоугольник (перевод с греч. ορθογώνιο.)Первые геометры мыслили прямоугольник вписанным в круг

Зал №6 КвадратОт латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого “тетрагонон” - четырехугольник.

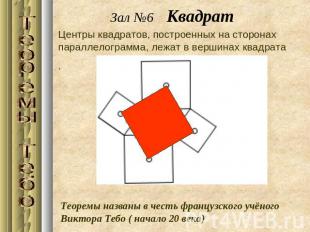
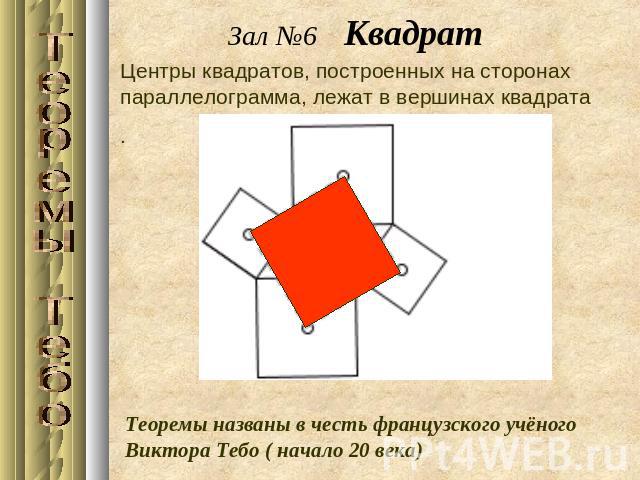
Зал №6 КвадратЦентры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата  . Теоремы названы в честь французского учёного Виктора Тебо ( начало 20 века)

Зал №6 КвадратЕсли на каждой из двух соседних сторон квадрата построить по равностороннему треугольнику (либо оба внутрь, либо оба вовне квадрата), то вершины этих двух треугольников, не являющиеся вершинами квадрата, и вершина квадрата, не являющаяся вершиной треугольников, образуют равносторонний треугольник.

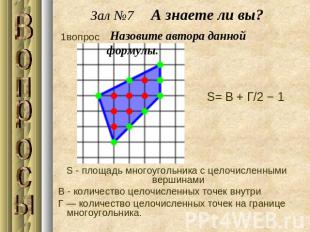
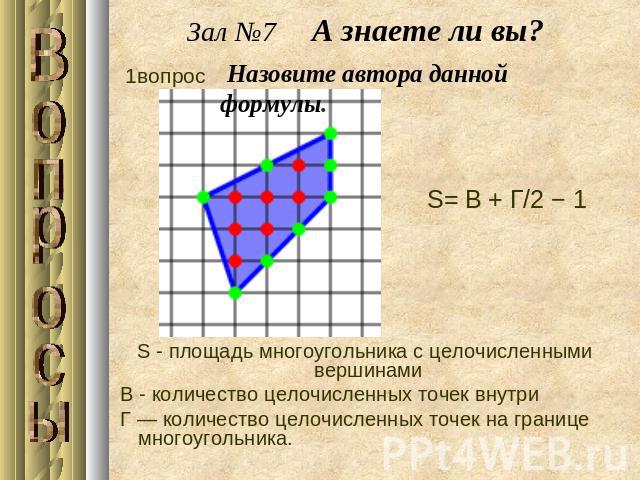
Зал №7 А знаете ли вы? Назовите автора данной формулы.S - площадь многоугольника с целочисленными вершинами В - количество целочисленных точек внутри Г — количество целочисленных точек на границе многоугольника.

Зал №7 А знаете ли вы?2 вопросКакая фигура называется дельтоидом3 вопросКакая мышца человека носит название четырёхугольника?

Литература: Литература:Я познаю мир. Математика сост. Савин А.П, Станцо В.В, Котова А.Ю. - АСТ, 1995 Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. - М.: Педагогика, 1989 Глейзер Г.И. История математики в школе. М.: Просвещение, 1981. Интернет ресурсы: http://pikalova-ms.narod.ru/portrety_matemaikov.htm http://www.biografguru.ru/by/matematik/?q=9&psn=76