Презентация на тему: Алгебраические дроби 8 класс


Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Алгебраические дроби». Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Алгебраические дроби». б). Закрепление навыков решения тестовых заданий по данной теме. Развивающие: а). Формирование и развитие умения мыслить и анализировать. б). Развитие памяти. Воспитывающие: а). Воспитание умения работать самостоятельно. б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания. в). Привитие интереса к предмету.

Алгебраическая дробь – выражение , где Алгебраическая дробь – выражение , где многочлен Р(х)-числитель алгебраической дроби, а Q(х)-ее знаменатель. 2. Основное свойство алгебраической дроби – и числитель и знаменатель алгебраической дроби можно умножить (разделить) на один и тот же не равный 0 многочлен. 3. Рациональное уравнение – уравнение вида =0, где Q(х)≠0. 4. Степень с отрицательным показателем - ,где n – натуральное число и а≠0.

1. Разложить все знаменатели на множители. 1. Разложить все знаменатели на множители. 2. Найти наименьшее общее кратное для числовых коэффициентов. 3. Составить произведение, включив в него НОК коэффициентов и все буквенные множители. Одинаковые множители берем один раз. Из всех степеней с одинаковым основанием берем множитель с наибольшим показателем степени.

Первый этап. Первый этап. 4а2-1=(2а-1)(2а+1) 2а2+а=а(2а+1) Общий знаменатель: а(2а-1)(2а+1) Дополнительные множители: К первой дроби: а Ко второй дроби: (2а-1)

Умножение: Умножение: Деление: Возведение в степень:

Тождества справедливы для а≠0, b≠0, s,t – произвольные целые числа. Тождества справедливы для а≠0, b≠0, s,t – произвольные целые числа. as · at = as + t as : at = as – t (as)t = ast (ab)s = as · bs (a : b)s = as : bs






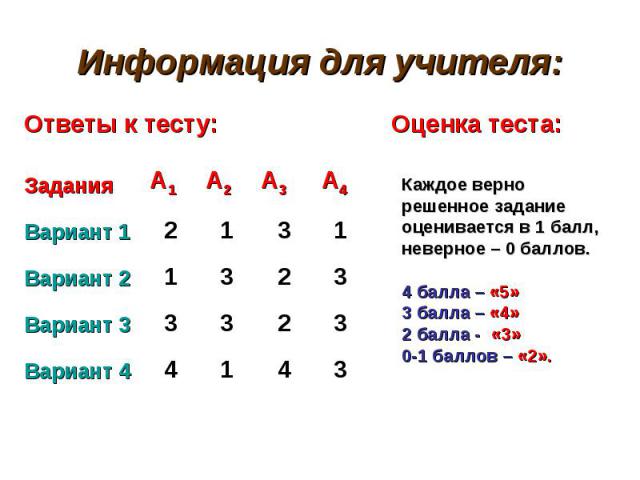
Ответы к тесту: Оценка теста: Ответы к тесту: Оценка теста:

«Алгебра 8 класс», часть 1, учебник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г. «Алгебра 8 класс», часть 1, учебник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г. «Алгебра 8 класс», часть 2, задачник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г. «Тематический сборник тестовых заданий по алгебре для подготовки к государственной (итоговой) аттестации в новой форме», базовый уровень, под редакцией Е.А. Семенко, Просвещение-Юг, Краснодар, 2008 г. «Экзаменационные тестовые задания», Федеральная служба по надзору в сфере образования и науки РФ, 2008 г. «Краевые диагностические работы по алгебре в 9 классе», Департамент образования и науки Краснодарского края, ККИДППО, 2008 г.