Презентация на тему: Виды чисел

Повторить понятия натуральных, целых, рациональных чисел Повторить понятия натуральных, целых, рациональных чисел Объяснить понятие иррациональных чисел Развивать умения различать множества чисел Научить выполнять действия с иррациональными числами

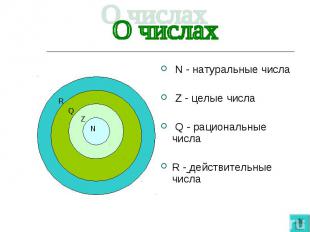
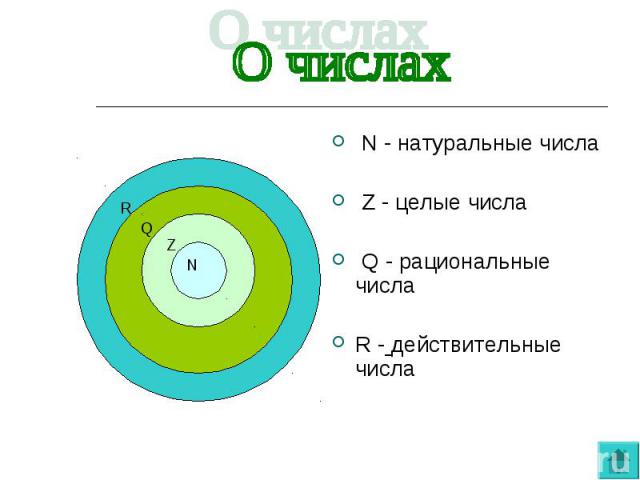
 N - натуральные числа  N - натуральные числа  Z - целые числа  Q - рациональные числа   R - действительные числа

N - натуральные числа  N - натуральные числа       Числа 1, 2, 3, …, употребляемые при счете предметов, образуют множество натуральных чисел. Обозначают буквой N. Например, запись 27Є N читается: «27 принадлежит множеству натуральных чисел». Любое натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9. Например, запись 2457 означает, что 2457=2•1000+4•100+5•10+7. Вообще если а - цифра тысяч, b –цифра сотен, d- цифра десятков и c- цифра единиц то имеем а • 1000+b•100+c•10+d. Используется также сокращенная запись аbcd.

Целые числа Целые числа Натуральные числа, противоположные им числа и число нуль Составляют множество целых чисел. Обозначают буквой Z. Например, запись -27Є Z читается: «-27 принадлежит множеству целых чисел».

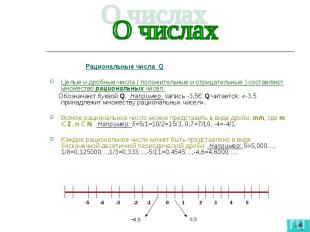
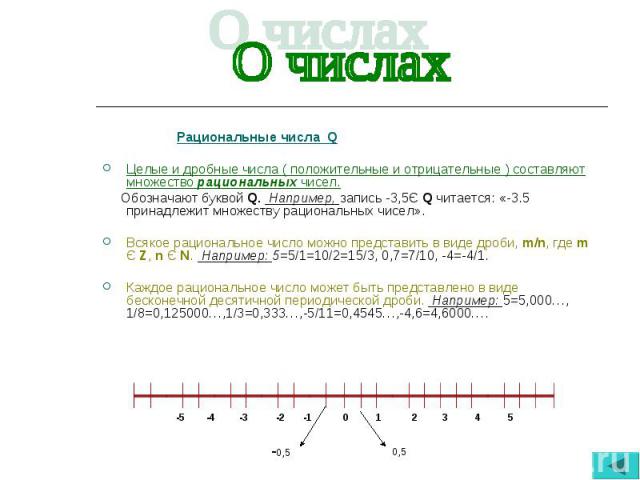
Рациональные числа Q Рациональные числа Q Целые и дробные числа ( положительные и отрицательные ) составляют множество рациональных чисел. Обозначают буквой Q. Например, запись -3,5Є Q читается: «-3.5 принадлежит множеству рациональных чисел». Всякое рациональное число можно представить в виде дроби, m/n, где m Є Z, n Є N. Например: 5=5/1=10/2=15/3, 0,7=7/10, -4=-4/1. Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Например: 5=5,000…, 1/8=0,125000…,1/3=0,333…,-5/11=0,4545…,-4,6=4,6000….

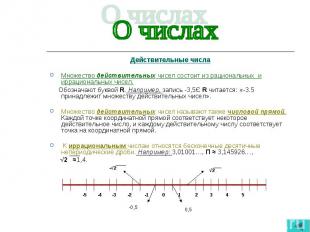
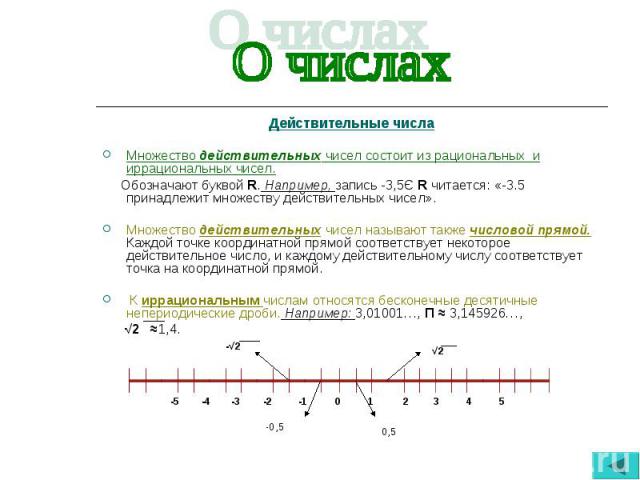
Действительные числа Действительные числа Множество действительных чисел состоит из рациональных и иррациональных чисел. Обозначают буквой R. Например, запись -3,5Є R читается: «-3.5 принадлежит множеству действительных чисел». Множество действительных чисел называют также числовой прямой. Каждой точке координатной прямой соответствует некоторое действительное число, и каждому действительному числу соответствует точка на координатной прямой. К иррациональным числам относятся бесконечные десятичные непериодические дроби. Например: 3,01001…, П ≈ 3,145926…, √2 ≈1,4.

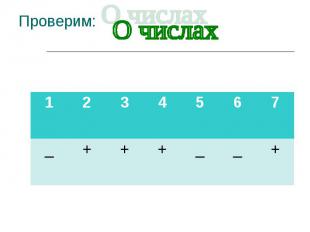
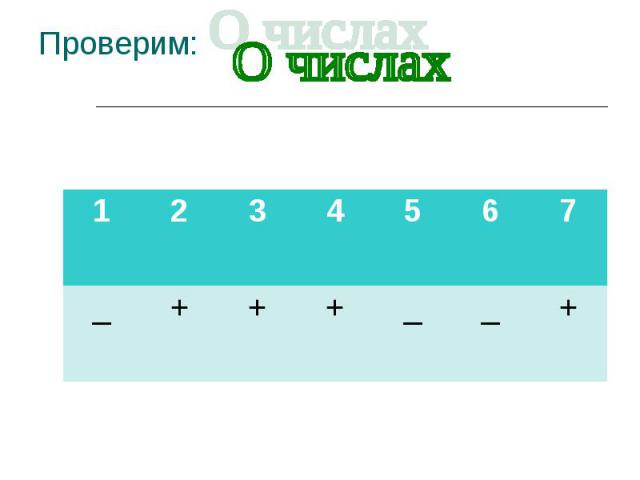
Выпишите при помощи знаков верные утверждения: Выпишите при помощи знаков верные утверждения: Число 6 является целым числом -4 является рациональным числом 6,5 является рациональным 10,1 является натуральным 13,(7) является рациональным -14,101 является целым 73 является натуральным и рациональным 3,7(2) является целым и рациональным

13,(2); -56; 8,23; -3,9; 34; 2,10010001….; 13,(2); -56; 8,23; -3,9; 34; 2,10010001….;

Всякое целое число является натуральным Всякое целое число является натуральным Всякое натуральное число является рациональным Число -7 является рациональным Сумма двух натуральных чисел всегда есть число натуральное Разность двух натуральных чисел есть число натуральное Действительное число не может быть натуральным Всякое иррациональное число является действительным