Презентация на тему: Множество чисел

Натуральные числа и действия над ними Натуральные числа и действия над ними Делимость. Простые и составные числа Наибольший общий делитель и наименьшее общее кратное Задачки Понятие множества, пересечение и объединение множеств Одночлены и многочлены Разложение многочлена на множители Формулы сокращённого умножения Подумай и реши Задания Авторы

Натуральные числа в порядке возрастания можно записать в виде последовательности 1, 2, 3, 4,… Множество всех натуральных чисел обозначается через N. Натуральные числа в порядке возрастания можно записать в виде последовательности 1, 2, 3, 4,… Множество всех натуральных чисел обозначается через N. Для натуральных чисел определены арифметические операции(сложение, вычитание, умножение и деление), возведение в Степень(число а в степени n, аn – это результат умножения числа а на себя n раз), обратная операция к возведению в степень – извлечение корня (b = ⁿ√а , если а = bⁿ) Сложение и умножение удовлетворяют переместительному закону(закону коммутативности): a + b = b + a , a · b=b · a и сочетательному закону (закону ассоциативности): (a + b ) + c = a + (b + c), (a · b) · c = a · (b · c), а также распределительному (дистрибутивному) закону: (a + b) · c = a · c + b · c

Найдите НОД двух чисел: Найдите НОД двух чисел: 1. 45 ; 135 2. 84 ; 168 3. 5 ; 60 Найдите НОК двух чисел: 1. 4 ; 5 2. 6 ; 7 3. 7 ; 8.

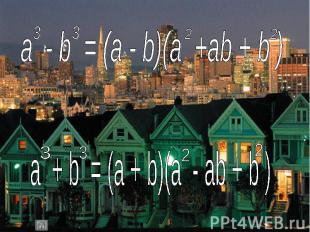
Простое число Простое число Составное число Набольший общий делитель Наименьшее общее кратное Взаимно простые числа Элемент множества Пересечение множеств Объединение множеств