Презентация на тему: Системы счисления

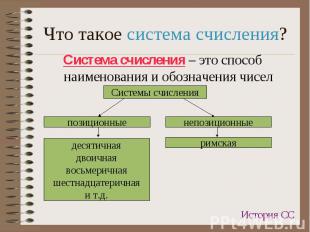
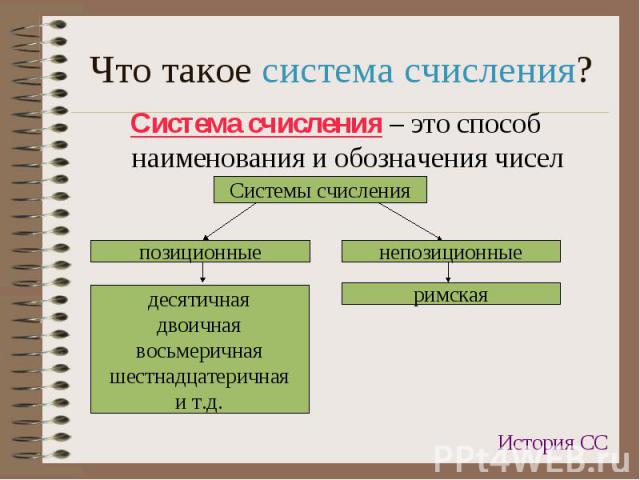
Система счисления – это способ наименования и обозначения чисел Система счисления – это способ наименования и обозначения чисел

Знаки (символы), используемые в СС для обозначения чисел, называются цифрами Знаки (символы), используемые в СС для обозначения чисел, называются цифрами

Является непозиционной, т.е. каждый символ обозначает всегда одно и тоже число; Является непозиционной, т.е. каждый символ обозначает всегда одно и тоже число; Цифры обозначаются латинскими буквами: I, V, X, L, C, D, M (1, 5, 10, 50, 100, 500, 1000) Например: XXX – 30; XLI - 41

Основанием системы может быть любое натуральное число, большее единицы; Основанием системы может быть любое натуральное число, большее единицы; Основание ПСС – это количество цифр, используемое для представления чисел; Значение цифры зависит от ее позиции, т.е. одна и та же цифра соответствует разным значениям в зависимости от того, в какой позиции числа она стоит; Например: 888: 800; 80; 8 Любое позиционное число можно представить в виде суммы степеней основания системы.

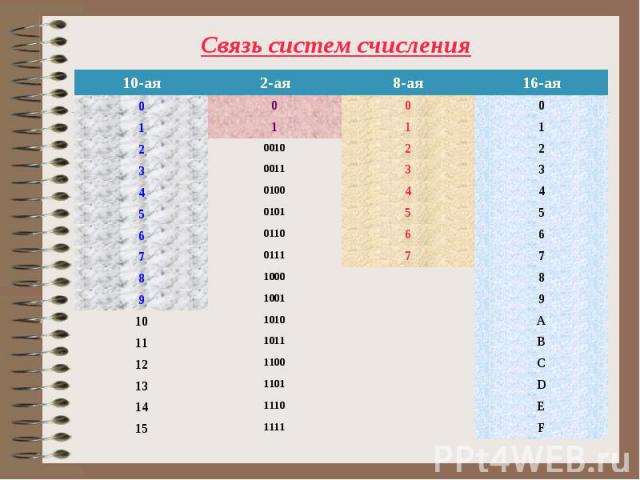
Основание системы – число 10; Основание системы – число 10; Содержит 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; Любое десятичное число можно представить в виде суммы степеней числа 10 – основания системы;

Основание системы – 2; Основание системы – 2; Содержит 2 цифры: 0; 1; Любое двоичное число можно представить в виде суммы степеней числа 2 – основания системы; Примеры двоичных чисел: 111001012; 101012;

Из десятичной СС в двоичную СС: Из десятичной СС в двоичную СС: Разделить десятичное число на 2. Получится частное и остаток. Частное опять разделить на 2. Получится частное и остаток. Выполнять деление до тех пор, пока последнее частное не станет меньшим 2. Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

Примеры: Примеры:

Задание № 1 Задание № 1 Для десятичных чисел 341; 125; 1024; 4095 выполни перевод в двоичную систему счисления. проверка

Для перехода из двоичной системы счисления в десятичную необходимо двоичное число представить в виде суммы произведений цифр числа на основание (2) в степени, соответствующей месту цифры и найти ее десятичное значение. Для перехода из двоичной системы счисления в десятичную необходимо двоичное число представить в виде суммы произведений цифр числа на основание (2) в степени, соответствующей месту цифры и найти ее десятичное значение. Пример:

Двоичные числа 10110012, 111102, 110110112 перевести в десятичную систему. Двоичные числа 10110012, 111102, 110110112 перевести в десятичную систему. проверка

Основание системы – 8; Основание системы – 8; Содержит 8 цифры: 0; 1; 2; 3; 4; 5; 6; 7; Любое восьмеричное число можно представить в виде суммы степеней числа 8 – основания системы; Примеры восьмеричных чисел: 21058; 734618;

Основание системы – 16; Основание системы – 16; Содержит 16 цифр: от 0 до 9; A; B; C; D; E; F; Любое шестнадцатеричное число можно представить в виде суммы степеней числа 16 – основания системы; Примеры шестнадцатеричных чисел: 21AF316; B09D16;

Разделить десятичное число на p. Получится частное и остаток. Разделить десятичное число на p. Получится частное и остаток. Выполнять деление до тех пор, пока последнее частное не станет меньше p. Записать остатки в обратном порядке. Полученное число и будет p-i записью исходного десятичного числа.

Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему. Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему. проверка

Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему. Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему.

Умножить десятичную дробь на p. Умножить десятичную дробь на p. Целую часть выписать, с дробной продолжить умножение до тех пор, пока она не станет равной 0 или не выделится в период Выписать целые части сверху-вниз. Полученное число и будет p-i записью исходного десятичного числа.

Десятичные числа Десятичные числа 0,51; 0,125 перевести в 8 и 16 системы счисления.

Для перевода из p-i системы счисления в q-i число надо сначала перевести из p-i системы счисления в 10 систему счисления (развернутая форма числа), а затем из 10СС в q-i (деление целой и умножение дробной части) Для перевода из p-i системы счисления в q-i число надо сначала перевести из p-i системы счисления в 10 систему счисления (развернутая форма числа), а затем из 10СС в q-i (деление целой и умножение дробной части)

Восьмеричные числа 41, 520, 306 перевести в десятичную систему. Восьмеричные числа 41, 520, 306 перевести в десятичную систему.

Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему. Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему.

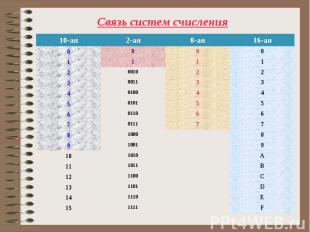
Переводы в системах счисления с основанием кратным 2 Переводы в системах счисления с основанием кратным 2

Разбить двоичное число на триады справа налево (целая часть) и слева направо (дробная часть) от запятой (по три цифры). Заменить каждую триаду соответствующей восьмеричной цифрой. Разбить двоичное число на триады справа налево (целая часть) и слева направо (дробная часть) от запятой (по три цифры). Заменить каждую триаду соответствующей восьмеричной цифрой.

Двоичные числа 101011,112 ; 110011001,102 перевести в восьмеричную систему Двоичные числа 101011,112 ; 110011001,102 перевести в восьмеричную систему

Разбить двоичное число на тетрады (по четыре цифры) справа налево для целой части и слева-направо для дроби. Заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Разбить двоичное число на тетрады (по четыре цифры) справа налево для целой части и слева-направо для дроби. Заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

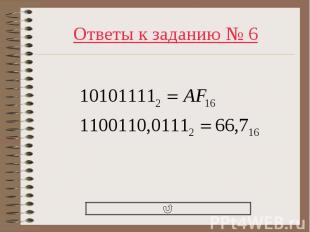
Двоичные числа 101011112 ; 1100110,01112 перевести в шестнадцатеричную систему Двоичные числа 101011112 ; 1100110,01112 перевести в шестнадцатеричную систему проверка

Каждую восьмеричную цифру заменить соответствующим двоичным кодом по три цифры в каждом Каждую восьмеричную цифру заменить соответствующим двоичным кодом по три цифры в каждом

Восьмеричные числа 26, 702, 4017 перевести в двоичную систему. Восьмеричные числа 26, 702, 4017 перевести в двоичную систему.

Каждую шестнадцатеричную цифру заменить двоичным кодом по четыре цифры в каждом Каждую шестнадцатеричную цифру заменить двоичным кодом по четыре цифры в каждом

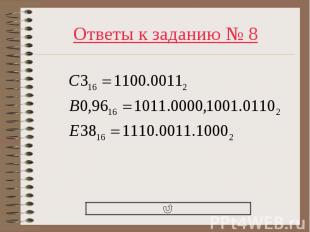
Шестнадцатеричные числа C3; B0,96; E38 перевести в двоичную систему. Шестнадцатеричные числа C3; B0,96; E38 перевести в двоичную систему. проверка