Презентация на тему: Системы счисления 10-11 класс

Информатика и ИКТ 10-11 класс Системы счисления

Система счисления – это способ наименования и представление чисел с помощью символов. Такие символы в любой системе счисления называются цифрами. Алфавит системы счисления – это совокупность символов, используемых в данной системе счисления.

Системы счисления непозиционные Система счисления, в которой значение цифры не зависит от ее позиции в записи числа. Н-р: римская система счисления, алфавитная система счисления. Римская система счисления I VX L C DM 1 5 10 50 100 500 1000 позиционные Система счисления, в которой значение цифры зависит от ее позиции в записи числа. К позиционным системам счисления относятся десятичная, двоичная, восьмеричная, двенадцатеричная, шестнадцатеричная и др. Основание позиционной системы счисления (q) – количество символов, используемых для записи числа.

Римская система счисления Задание: 1. Переведите числа из римской системы счисления в десятичную – LXXXVI. XLIX. CMXCIX. 2. Запишите десятичные числа в римской системе счисления – 464, 390, 2648. 3. Где в настоящее время используется римская система счисления.

Укажите какие числа записаны с ошибками. Ответ обоснуйте. 1567; 3005,234; 185,7948; 11022; 1345,526; 112,0113; 16,5455.

В любой системе счисления натуральные числа, меньшие основания q, представляются с помощью одной цифры данной системы. Если число больше или равно q, то требуется две и более цифр. Представление первых чисел в некоторых системах счисления Задание: заполните таблицу для q=6.

Представление чисел в позиционных системах счисления разряды 2 1 0 -1 -2 N10 = 3 4 8, 1 2 = 3*102 + 4*101 + 8*100 + 1*10-1 + 2*10-2 Свернутая форма записи числа развернутая форма записи числа Любое действительное число можно записывать в любой позиционной системе счисления в виде суммы положительных и отрицательных степеней числа q (основания системы). Задание5: Запишите в развернутой форме числа:N8=7764,1=N5=2430,43= Задание6: Запишите число в десятичной системе счисления: 110112=……, 423,15=……, 5А,12116=……. Пример: 1011,012=1*23+0*22+1*21+1*20+0*2-1+1*2-2=8+2+1+¼=11 ¼.

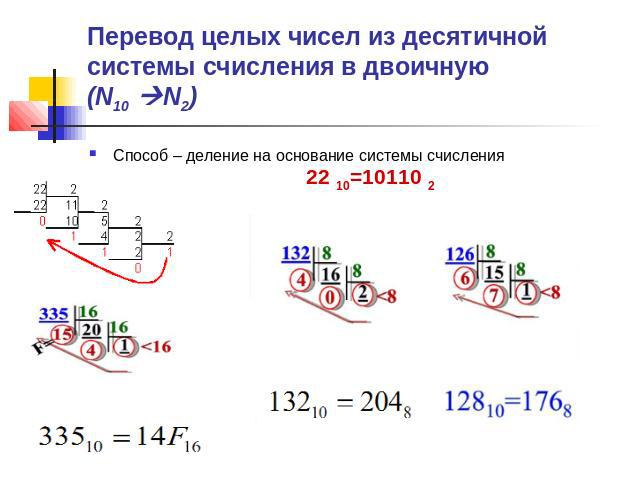
Перевод целых чисел из десятичной системы счисления в двоичную (N10 N2) Способ – деление на основание системы счисления

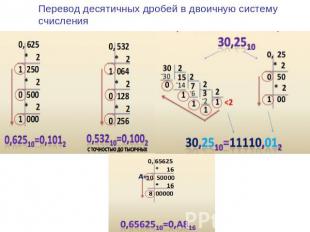
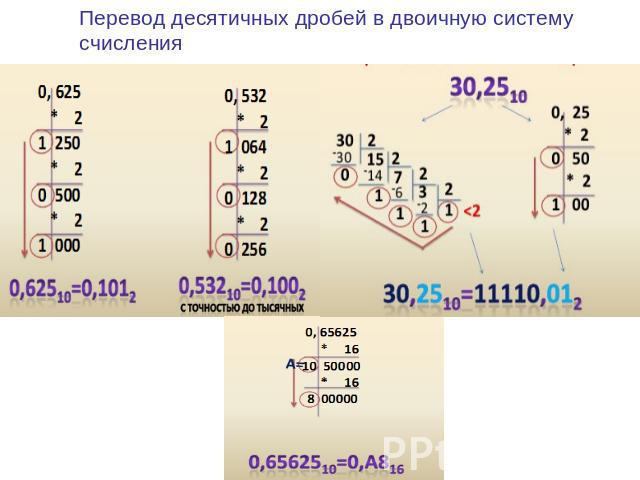
Перевод десятичных дробей в двоичную систему счисления

Перевод десятичных дробей в двоичную систему счисления (N10 N2) (умножением на 2) Пример: 0,562510 = N2 = 0,10012 Задание 10: переведите десятичные дроби в двоичную систему счисления с точностью до 6 знаков после запятой: 0,710 0,4622100,5198100,580310

Перевод смешанных чисел из десятичной системы счисления в двоичную Алгоритм перевода: 1) перевести целую часть; 2) перевести дробную часть; 3) сложить полученные результаты. Пример :перевести 17,2510 в двоичную систему счисления. Решение: 1710 = 100012 0,2510= 0,012 17,2510 = 10001,012 Задание 11: переведите в двоичную систему счисления числа: 40,510

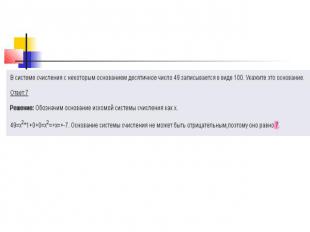
Задание. В системе счисления с некоторым основанием десятичное число 12 записывается как 110. Найдите это основание. Решение. Сначала распишем число 110 через формулу записи чисел в позиционных системах счисления для нахождения значения в десятичной системе счисления, а затем найдем основание методом перебора. Значит основание системы счисления равно 3. Ответ. Искомое основание системы счисления равно 3.